CPT Symmetry: General Symmetry of Nature

By O.W. Greenberg
Since Albert Einstein's seminal paper of 1905 on the special theory of relativity, Lorentz covariance has been recognized as one of the basic requirements of any fundamental physical theory. Nonetheless, one must allow the possibility that this property will be violated at some scale of energy or at some range of distance for which this property has not yet been tested.
To date, despite many theoretical ideas and many experimental tests, no violation of Lorentz covariance has been detected. The Lorentz group, without space or time inversion or any combination of these inversions, is a continuous and connected group of transformations. One can ask if there are symmetries of nature that have the same general validity as Lorentz covariance but are not continuously connected to the identity transformation. Surprisingly, there is precisely one such symmetry-CPT symmetry. In CPT symmetry, space is inverted, time is reversed without changing the sign of the energy of physical states and particle-and-antiparticle are interchanged. The quantities position (r), momentum (p), charge (q), angular momentum (L) and magnetic moment (μ) transform as
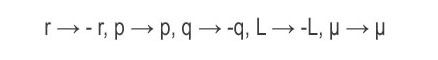
under CPT. xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
|
|
|
|
Albert Einstein |
Wolfgang Pauli |
Eugene Wigner |
Res Jost |
This note will give plausible argument for the general validity of CPT symmetry in any Lorentz covariant theory of nature. Wolfgang Pauli gave a proof of CPT symmetry in the language of Lagrangian Quantum Field Theory in Niels Bohr and the Development of Physics (McGraw-Hill, NY: 1955) , and Res Jost gave a rigorous proof of CPT symmetry in the language of axiomatic quantum field theory in Helvetica Physcia Acta (30, 409-416 :1957).
We start the observation that space-time inversion, in which x° ≡ t → -t and x → - x, is continuously connected to the identity. To see this, rotate by π in any plane in four-dimensional space-time and rotate again by π in the orthogonal plane; for example in the x ¹ - x ² plane and in the x º - x ³ plane. This space-time inversion symmetry cannot be considered a symmetry of nature because the transformation t→ - t reverses the sign of the energy of a physical state.
With the usual sign convention, a state of positive energy E evolves under time as e -iEt. If the sign of time were inverted as a unitary transformation, the state would evolve as e iEt , which would correspond to a state of energy - E . Eugene P. Wigner recognized that to correct this problem time inversion must be replaced by time reversal, in which t→ - t and states and complex numbers are complex conjugated. Such a transformation is an anti-unitary transformation. The combination of time inversion and complex conjugation preserves the sign of the energy and allows Wignerian time reversal to be a symmetry of a physical state. Because unitary and anti-unitary transformations are not connected, space-time inversion together with complex conjugation, is a discrete symmetry that is not connected to the group of Lorentz transformations. The complex conjugation, carried out on the space of physical states of quantum mechanics, corresponds to the particle-anti-particle interchange that we call charge conjugation. Thus space-time inversion, together with complex conjugation, is the general symmetry of nature that we call CPT symmetry.
The jump from the unitary four-dimensional space-time inversion that is connected to the identity, but is not a physical symmetry to the anti-unitary CPT symmetry that is a physical symmetry but is not connected to the identity requires a demonstration. This demonstration uses properties of quantum field theory including the positivity of the energy spectrum of the theory and the commutativity for Bose fields (or anticommutativity for Fermi fields) at a subset of points in space-time that are separated by a space like distance, the "Jost points." We refer the reader who wants to understand the fundamental CPT symmetry better to Jost's paper.
|
