Research Summary

This document discusses the highlights of my research career.  Each section provides a brief introduction to the physics issues, but makes no attempt to review those subjects or to cite the most definitive literature.  Instead, I cite the most significant of my own contributions only, where the numbering restarts in each section.  Although there is overlap, the major topics are arranged roughly in reverse chronological order; several minor topics are omitted.  A complete list of my publications is provided at publications.

Along the way, I developed several software packages and have made some of them available to other researchers.

Pion electroproduction

Transition form factors for electroexcitation of nucleon resonances provide important tests of models of hadronic structure; furthermore, one hopes that accurate QCD calculations will soon become available for these quantities. These form factors are usually deduced from analyses of resonant electroproduction of pseudoscalar mesons, but such analyses are complicated by nonresonant mechanisms, final-state interactions, and the overlap of several broad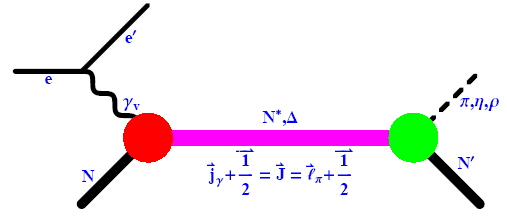 resonances. Therefore, it is important to perform multipole analyses of both cross section and polarization data, rather than rely upon model calculations. Polarization observables depend upon interferences between various products of multipole amplitudes, which enhances the sensitivity to smaller contributions and provides the relative phases between those amplitudes. That information then helps to distinguish between resonant, nonresonant, and nondominant resonant contributions. A former student (T. Payerle) and I developed a code that evaluates recoil-polarization observables for pion electroproduction, epiprod, beginning in 1992. I then extended the code to include η production, target polarization, and to perform fits to comprehensive data sets using Legendre coefficients or complex multipole amplitudes. The code also includes interfaces to Monte Carlo simulations and provides pseudodata options for optimization of experimental proposals or for testing internal consistency.

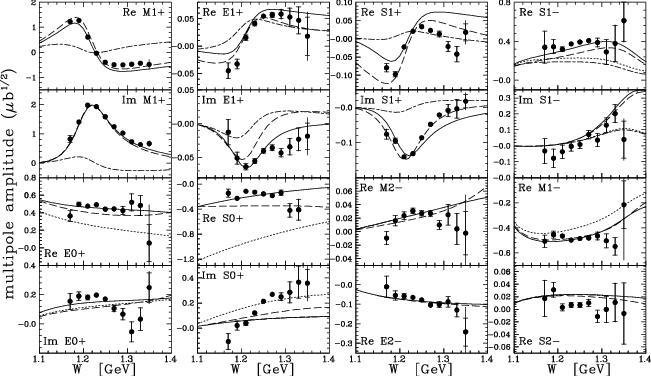
I led Jefferson Lab experiment e91011 that measured angular distributions of recoil polarization response functions for neutral pion electroproduction at Q2 = 1 (GeV/c)2 across the Δ(1232) resonance. [1,2] We obtained 16 independent response functions, 14 separated plus 2 Rosenbluth combinations, of which 12 were observed for the first time in any reaction. I performed the first nearly model-independent multipole analysis of polarization data for pion electroproduction [2] and obtained accurate quadrupole ratios for the N→Δ resonance that do not depend upon the assumptions of M1+ dominance and ℓπ≤1 truncation employed by the traditional Legendre analysis of differential cross sections. In fact, my detailed analysis of the Legendre method [3] demonstrates that these assumptions are inherently unreliable and that the fact that reasonably accurate results were obtained by that method results from a lucky conspiracy among many contributions of similar magnitude and varying sign. Multipole analysis of polarization data is much more stable because it provides both real and imaginary parts of the contributing amplitudes without model-dependent assumptions and it does not rely upon cancellations.  Data tables, Legendre coefficients, multipole amplitudes and other information can be obtained from e91011.

I also implemented a unitary isobar model that permits one to distinguish between resonant and nonresonant contributions to various partial waves. Thus, we see evidence in the 1- multipoles of predominantly longitudinal excitation of the Roper resonance. [2] This is consistent with the interpretation of this state as a radial excitation of the nucleon and tends to exclude hybrid models with significant excitation of the gluon field. This model also suggests that the πNN coupling is dominantly pseudovector and is inconsistent with a recently proposed interpolation between pseudovector coupling at low momenta and pseudoscalar coupling at higher momentum.

References

  1. Recoil Polarization for Delta Excitation in Pion Electroproduction, J. J. Kelly et al., Phys. Rev. Lett. 95, 102001 (2005)
  2. Recoil polarization measurements for neutral pion electroproduction at Q2 = 1 (GeV/c)2 near the Delta resonance, J. J. Kelly et al., nucl-ex/0509004 (submitted to Phys. Rev. C)
  3. Accuracy of traditional Legendre estimators of quadrupole ratios for the N→Δ transition, J. J. Kelly,  Phys. Rev. C 72, 048201 (2005)

Related publications

  1. Recoil Polarization for Neutral Pion Electroproduction near the Delta Resonance, J. J. Kelly,  Fizika B 13, 81 (2004)
  2. Backward electroproduction of π0 mesons on protons in the region of nucleon resonances at four momentum squared Q2=1.0 GeV2, G. Laveissiere et al., Phys. Rev. C 69, 045203 (2004)
  3. Polarization measurements in neutral pion photoproduction, K. Wijesooriya et al., Phys. Rev. C 66, 034614 (2002)
  4. Search for Quadrupole Strength in the Electroexcitation of the Δ+(1232), C. Mertz et al., Phys. Rev. Lett. 86, 2963 (2001)
  5. Measuring longitudinal amplitudes for electroproduction of pseudoscalar mesons using recoil polarization in parallel kinematics, J. J. Kelly,  Phys. Rev. C 60, 054611 (1999)
  6. Recoil polarization in electroproduction of mesons, J. J. Kelly, Fizika B 8, 81 (1999)
  7. Induced proton polarization for π0 electroproduction at Q2 =0.126 (GeV/c)2 around the Δ(1232) resonance, G. A. Warren et al., Phys. Rev. C 58, 3722 (1998)

Nucleon form factors

Nucleon electromagnetic form factors provide important tests of models of nucleon structure and hopefully accurate lattice QCD calculations will become available soon. Accurate measurements of these form factors are also needed for many applications in nuclear physics and even for studies of parity violation in atomic physics. Although magnetic form factors can be obtained from cross section measurements, it becomes increasingly difficult to obtain precise data for electric form factors as Q2 increases. Indeed, the model dependence for extractions of the neutron electric form factor, GEn, from cross section data are so severe that it is fair to say that no reliable data existed for that quantity prior to 1994. Fortunately, the electric form factor contributes linearly to transverse recoil or target polarization for quasifree nucleon scattering, which makes accurate measurements possible with minimal model dependence. Therefore most recent high-precision measurements have relied upon polarized electron scattering.

Neutron electric form factor

I was a major participant in the first proof-of-principle for this technique [1], where GEn was measured at MIT-Bates using the d(e-pol,e' n-pol)p reaction at Q2 = 0.255 (GeV/c)2. An upgraded polarimeter was then used in Jefferson Lab experiment e93038 to measure GEn at Q2 = 0.45, 1.13, and 1.45 (GeV/c)2 with very small systematic uncertainties and statistics of about 7%, both the highest Q2 and the best precision obtained to date. [2,3]  I led the analysis team, wrote the time calibration and event reconstruction software for the neutron polarimeter, and supervised the development of a full-scale simulation program, much of which I wrote myself. I also played a significant role in JLab experiment e93026 which used the asymmetry for a polarized 15ND3 target to measure GEn at Q2 = 0.5 and 1.0 (GeV/c)2 [4] and supervised PhD thesis of N. Savvinov. Good agreement was obtained between the results from these quite different techniques.  I now participate in JLab experiment e02013 which uses a polarized 3He target to obtain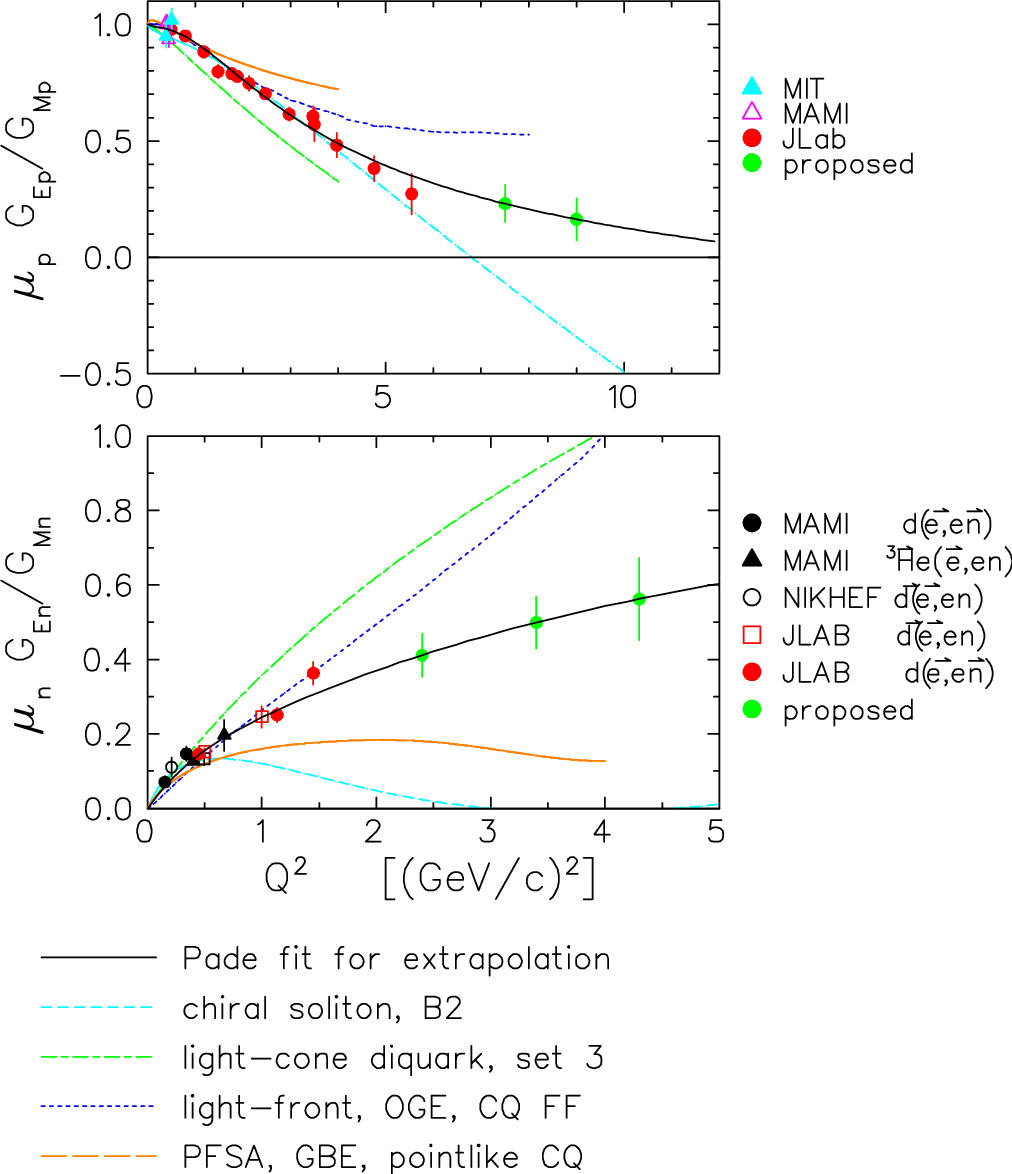 data for  Q2 = 2.4 and 3.4 (GeV/c)2.  Data taking was completed in May 2006 and analysis is in progress.  The figure at right compares recent polarization data (red) with predictions of several models, which spread out rapidly as Q2 increases.  The green points show the statistics expected for proposed experiments based upon a fit to existing data.

Proton electromagnetic ratio
 

One of the first experiments to be performed in Hall A of Jefferson Lab measured the ratio of electric and magnetic form factors for the proton, GEp/GMp.  [5,6] The experiment was designed primarily as a calibration of the new focal-plane polarimeter and almost everyone expected the form factor ratio to be close to unity over the entire range of Q2, consistent with previous SLAC results but with higher precision.  Contrary to these expectations, the ratio for Q2>1 decreased rapidly and nearly linearly.  Although some models had predicted this behavior, the data were still surprising because they contradicted trusted data using the Rosenbluth (cross section) technique.  Later experiments [7,8] extended these results to higher Q2 and confirmed the linear behavior. These data are shown as red points.  In the meantime, a new "super-Rosenbluth" experiment confirmed the early Rosenbluth results.  Therefore, the Rosenbluth and polarization transfer techniques definitely disagree.  It is now believed that previously-neglected two-photon contributions are responsible for this discrepancy, with the effect being much larger for the cross section than for polarization.  Several recent and future experiments study the two-photon mechanism and many theorists are attempting to calculate these effects more accurately.  Furthermore, the green points show the statistics anticipated for an upcoming experiment, based upon a fit to the existing data.

 

Charge and magnetization densities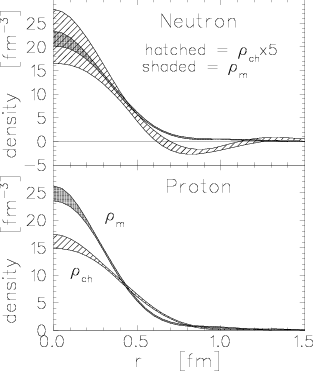

Nonrelativistically the Sachs electric and magnetic form factors are simply Fourier transforms of the charge and magnetization densities of the nucleon. Although this intuitively appealing relationship is not relativistically invariant, it is still interesting to parametrize the form factors using radial densities. I developed a model [9] that incorporates Lorentz contraction, is consistent with dimensional scaling at large Q2, and expands nucleon charge and magnetization densities using complete sets of radial basis functions; thus, one obtains radial densities with realistic error envelopes.Thus, I found that recoil polarization data for the proton  show that the charge density is broader than the magnetization density for the proton. Similarly, the magnetization density is slightly broader for the neutron than for the proton. Combining neutron and proton charge densities, I used a two-flavor model to deduce u and d quark radial distributions and find in the proton a slightly broader u than d distribution and a statistically significant negative d density near 1 fm that might be attributed to the d content of the pion cloud. Finally, I also developed a simpler Padè parametrization of nucleon form factors that is more convenient for applications. [10]

References

  1. Electric form factor of the neutron from the 2H(e,e'n)1H reaction at Q2=0.255 (GeV/c)2, T. Eden et al., Phys. Rev. C 50, R1749 (1994)
  2. Measurements of GEn/GMn from the 2H(e,e'n)1H Reaction to Q2 = 1.45 (GeV/c)2, R. Madey et al., Phys. Rev. Lett. 91, 122002 (2003)
  3. Measurements of the neutron electric to magnetic form factor ratio GEn/GMn via the 2H(e,e'n)1H reaction to Q2 = 1.45 (GeV/c)2, B. Plaster et al., Phys. Rev. C 73, 025205 (2006)
  4. Measurement of the Electric Form Factor of the Neutron at Q2 = 0.5 and 1.0 GeV2/c2, G. Warren et al., Phys. Rev. Lett. 92, 042301 (2004)
  5. GEp/GMp Ratio by Polarization Transfer in e-vector p → ep-vector, M. K. Jones et al., Phys. Rev. Lett. 84, 1398 (2000)
  6. Proton elastic form factor ratios to Q2 = 3.5 GeV2 by polarization transfer, V. Punjabi et al., Phys. Rev. C 71, 055202 (2005)
  7. Measurements of the elastic electromagnetic form factor ratio µGEp/GMp via polarization transfer, O. Gayou et al., Phys. Rev. C 64, 038202 (2001)
  8. Measurement of GEp/GMp in e-vector p → ep-vector to Q2=5.6 GeV2, O. Gayou et al., Phys. Rev. Lett. 88, 092301 (2002)
  9. Nucleon charge and magnetization densities from Sachs form factors, J. J. Kelly, Phys. Rev. C 66, 065203 (2002)
  10. Simple parametrization of nucleon form factors, J. J. Kelly, Phys. Rev. C 70, 068202 (2004)

Related publications

  1. Measurement of the magnetic form factor of the neutron, P. Markowitz et al., Phys. Rev. C 48, R5 (1993)
  2. Performance of a neutron polarimeter to measure the electric form factor of the neutron, T. Eden et al., Nucl. Instrum. Meth. A 338, 432 (1994)
  3. Neutron detection efficiency for the measurement of the 2H(e,e'n)1H cross section, T. Eden et al., Nucl. Instrum. Methods A 405, 60 (1998)
  4. Comparison of polarization observables in electron scattering from the proton and deuteron,  B. D. Milbrath et al., Phys. Rev. Lett. 80, 452 (1998)
  5. Parity-violating electroweak asymmetry in ep scattering, K. A. Aniol et al., Phys. Rev. C 69, 065501 (2004)

 

Nucleon knockout by electron scattering

Nucleon knockout by electron scattering provides a powerful probe of the electromagnetic properties of nucleons and of the momentum distributions in nuclei. Since the nucleus is transparent with respect to the electromagnetic interaction, the entire nuclear volume can be probed uniformly. The weakness of the electromagnetic interaction allows one to separate the soft Coulomb distortion of the electron scattering process from the hard-scattering event in which, to a very good approximation, a single virtual photon transfers its energy and momentum to the nuclear electromagnetic current. The kinematic flexibility of electron scattering permits the momentum and energy transfers to be varied independently, with various kinematical conditions emphasizing different aspects of the reaction mechanism. For example, under conditions in which a single high-energy nucleon receives most of the energy transfer, the quasifree electron-nucleon scattering process is emphasized.

In 1991-92 I used a sabbatical at NIKHEF-K (Netherlands) to learn the physics of (e,e' N) reactions and started working on a major review article that was published a few years later [1]. I expanded my LEA code to describe both (N,N') and (e,e' N) reactions in a consistent framework, using the local density approximation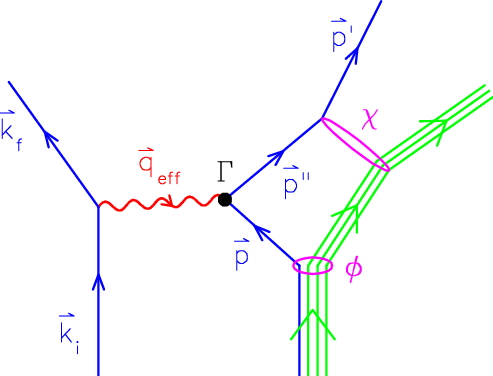 for the electromagnetic current and density dependence in the final-state interactions based upon my previous work on proton scattering. A microscopic coupled-channels method was implemented for both reactions [2,3]; mine is still the only code with that capability for the (e,e' N) reaction. In a subsequent series of papers I investigated the relationship between nuclear transparency and nucleon elastic scattering [4], gauge and Gordon ambiguities in the current operator [5], the radial dependence of the nucleon effective mass [6], the contributions of channel coupling at large missing momentum [7], sensitivity of electromagnetic knockout to density dependence of nucleon form factors [7], and the sensitivity of left-right asymmetry to dynamical enhancement of lower of Dirac spinors in the nuclear mean field [8,9]. The role of spinor distortion in (e,e' p) reactions is now well-established experimentally [9-11]. I performed the calculations that were compared with the first measurements of induced polarization for (e,e' p) and provided an intuitive explanation for the effect of the spin-orbit potential [12]. I made the first calculations of the sensitivity of polarization measurements for quasifree (e,e' N) to possible density dependence of nucleon form factors [8] and participated in experiments [13-15] that provided evidence for a small but apparently significant effect for the proton. I performed analyses of spectroscopic factors for 16O(e,e' p) [10,11] and 12C(e,e' p) [16], showing that consistent results are obtained using the relativistic distorted wave impulse approximation with little evidence for the Q2 dependence that was claimed by a previous nonrelativistic analysis. I also demonstrated consistency between exclusive and quasifree semi-inclusive 12C(e,e' p) [16].

References

  1. Nucleon knockout by intermediate energy electrons, J. J. Kelly, Adv. Nucl. Phys. 23, 75 (1996)
  2. Microscopic coupled-channels analysis of 9Be(p,p') for 100 ≤ Ep ≤ 500 MeV, J. J. Kelly, Phys. Rev. C 46, 711 (1992)
  3. Proton scattering off 9Be and the final-state interaction in the (e,e'p) and (γ,p) reactions on 10B , L. J. de Bever et al., Nucl. Phys. A579, 13 (1994)
  4. Nuclear transparency to intermediate-energy protons, J. J. Kelly, Phys. Rev. C 54, 2547 (1996)
  5. Gauge ambiguities in (e,e'N) reactions, J. J. Kelly, Phys. Rev. C 56, 2672 (1997)
  6. Radial dependence of the nucleon effective mass in 10B, L. J. de Bever et al., Phys. Rev. Lett. 80, 3924 (1998)
  7. Channel coupling in A(e,e' N)B reactions, J. J. Kelly, Phys. Rev. C 59, 3256 (1999)
  8. Effects of spinor distortion and density-dependent form factors upon quasifree 16O(e,e'p), J. J. Kelly, Phys. Rev. C 60, 044609 (1999)
  9. Influence of the Dirac sea on proton electromagnetic knockout, J. J. Kelly, Phys. Rev. C 72, 014602 (2005)
  10. Dynamical Relativistic Effects in Quasielastic 1p-Shell Proton Knockout from 16O, J. Gao et al., Phys. Rev. Lett. 84, 3265 (2000)
  11. Dynamics of the quasielastic 16O(e,e'p) reaction at Q2 =0.8 (GeV/c)2, K. G. Fissum et al., Phys. Rev. C 70, 034606 (2004)
  12. Measurement of the induced proton polarization Pn in the 12C(e,e'p) reaction, R. J. Woo et al., Phys. Rev. Lett. 80, 456 (1998)
  13. Polarization transfer in the 16O(e,e'p)15N reaction, S. Malov et al., Phys. Rev. C 62, 057302 (2000)
  14. Polarization transfer in the 4He(e,e'p)3H reaction, S. Dieterich et al., Phys. Lett. B 500, 47 (2001)
  15. Polarization Transfer in the 4He(e,e'p)3H Reaction up to Q2 = 2.6 (GeV/c)2, S. Strauch et al., Phys. Rev. Lett. 91, 052301 (2003)
  16. Relativistic distorted wave impulse approximation analysis of 12C(e,e'p) for Q2 < 2 (GeV/c)2, J. J. Kelly, Phys. Rev. C 71, 064610 (2005)

Related publications

  1. Reaction 12C(e,e'p) in the Dip Region, R. W. Lourie et al., Phys. Rev. Lett., 56, 2364 (1986)
  2. Missing-Energy Dependence of the Separated Response Functions for the Reaction 12C(e,e'p), P .E. Ulmer et al., Phys. Rev. Lett. 59, 2259 (1987)
  3. Neutron knockout and isobar excitation in quasi-free electron scattering, S. Boffi, M. Radici, J. J. Kelly and T. M. Payerle, Nucl. Phys. A539, 597 (1992)
  4. High-Momentum Protons in 208Pb, I. Bobeldijk et al., Phys. Rev. Lett. 73, 2684 (1994)
  5. Quasifree (e,e'p) reactions and proton propagation in nuclei, D. J. Abbott et al., Phys. Rev. Lett. 80, 5072 (1998).
  6. Measurements of the deuteron elastic structure function A(Q2) for 0.7 < Q2 < 6.0 (GeV/c)2 at Jefferson Laboratory, L. C. Alexa et al., Phys. Rev. Lett. 82, 1374 (1999)
  7. Separated spectral functions for the quasifree 12C(e,e'p) reaction, D. Dutta et al., Phys. Rev. C 61, 061602(R) (2000)
  8. Polarization Measurements in High-Energy Deuteron Photodisintegration, K. Wijesooriya et al., Phys. Rev. Lett. 86, 2975 (2001)
  9. Dynamics of the 16O(e,e'p) Reaction at High Missing Energies, N. Liyanage et al., Phys. Rev. Lett. 86, 5670 (2001)
  10. High energy angular distribution measurements of the exclusive deuteron photodisintegration reaction, E. C. Schulte et al., Phys. Rev. C 66, 042201(R) (2002)
  11. Quasielastic (e,e'p) reaction on 12C, 56Fe, and 197Au, D. Dutta et al., Phys. Rev. C 68, 064603 (2003)
  12. Measurement of the 3He(e,e'p)pn Reaction at High Missing Energies and Momenta, F. Benmokhtar et al., Phys. Rev. Lett. 94, 082305 (2005)
  13. Quasielastic 3He(e,e'p)2H  Reaction at Q2 = 1.5 GeV2 for Recoil Momenta up to 1 GeV/c, M. M. Rvachev et al., Phys. Rev. Lett. 94, 192302  (2005)

Review article

I have written a comprehensive review of this subject: Nucleon Knockout by Intermediate Energy Electrons, Advances in Nuclear Physics, Vol. 23, pp. 75-294 (ed. J.W. Negele and E. Vogt, Plenum Press, 1996).

Brief contents

  1. Introduction
  2. One-Photon Exchange Approximation
  3. Nucleon Form Factors
  4. Proton Knockout Experiments on Few-Body Systems
  5. Distorted Wave Analysis of (e,e'N) Reactions
  6. Spectral Functions from (e,e'p) on Complex Nuclei
  7. Studies of the Reaction Mechanism for Nucleon Knockout
  8. Conclusions

errata for book: errata.ps
errata for preprint: preprint_errata.ps

Effective interaction for nucleon-nucleus scattering

Nonrelativistic models

The nucleon-nucleon effective interaction depends quite strongly on the local density of nuclear matter within the interaction region. In the nonrelativistic theory of nuclear matter, the two primary sources of this density dependence are Pauli blocking between identical fermions and dispersive effects due to the mean field. The isoscalar spin-independent central component of the effective interaction is affected most strongly. The dominant effect in the real part of this component can be described as a short-ranged repulsive interaction that is proportional to density and which simulates the anticorrelation between identical particles. The dominant effect on the imaginary part can be described as a Pauli blocking correction, proportional to the square of the local Fermi momentum, which represents the reduction of the available phase space for scattering and hence of the total cross section.

My Ph.D thesis provided the first definitive evidence for the importance of medium modifications of the nucleon-nucleon interaction to the interpretation of nucleon-nucleus scattering data. Differential cross sections for inelastic scattering of 135 MeV protons were measured for several states of 16-O. [1,2] The nuclear structure for these transitions was determined using electron scattering measurements of the transition charge densities. [3]Calculations for proton scattering were performed using the local density approximation (LDA). States whose transition densities have strong interior contributions were shown to be particularly sensitive to the high-density properties of the effective interaction, whereas surface-peaked transition densities are more sensitive to the low-density properties. This analysis demonstrated that the density-dependent corrections to proton scattering can be quite large, particularly for interior transition densities, and are described very well using the LDA. Most previous analyses relied on elastic scattering measurements, but elastic scattering averages over the nuclear volume and is dominated by the surface region where the corrections are relatively small. The radial localization of transition densities endows inelastic scattering with much greater sensitivity to the density dependence of the effective interaction.

However, although nuclear-matter calculations of the effective interaction do provide a good qualitative description of the dominant effects, calculations using different approximation schemes lead to quantitative differences that are unacceptably large. Since the theory is not yet under adequate control, I have developed a parametrization which accurately reproduces the density dependencies of theoretical interactions but which is also suitable for phenomenological analysis of scattering data. [4] I have also developed an efficient method for fitting a linear expansion of the transition amplitude to scattering data for many states among several targets simultaneously. This method, and the code that implements it, is called LEA for linear expansion analysis. I performed and/or analyzed proton scattering experiments for several targets over a wide range of projectile energy and have constructed  empirical effective interactions (EEI) for nucleon scattering in the energy range 135-650 MeV. [5-11] I have shown that the effective interaction depends primarily upon density and is practically independent of target or state, thus validating the essential premise of the local density approximation. However, contrary to the naive expectation of the LDA, the effective interaction within a finite nucleus need not reduce to the free interaction at low density. A nucleon found in the surface is aware of the interior, and vice versa, so that density-dependent corrections persist at low densities and are not saturated in the interior (at least for light- and medium-weight nuclei).

My detailed comparisons of elastic and inelastic scattering demonstrate that the density dependence of normal-parity isoscalar interaction is stronger for inelastic than for elastic scattering, confirming the rearrangment contribution predicted by Cheon et al. The LEA algorithm includes a self-consistency cycle in which the distorted waves are generated using the same interaction that drives the inelastic transition, with the Cheon rearrangement factor included.

Relativistic models

In relativistic models of nucleon propagation through nuclear matter, the Dirac spinor is distorted by the scalar and vector mean fields. When reduced to Schrödinger-equivalent form, spinor distortion produces density-dependent contributions to the optical potential even for density-independent interactions. Since inelastic scattering requires distortion of four spinors, whereas elastic scattering distorts only three, the density dependence is automatically stronger for inelastic than for elastic scattering. Furnstahl and Wallace constructed an effective interaction based upon the IA2 version of the relativistic impulse approximation. Wallace and I extended the energy range, included Pauli blocking corrections and other smaller refinements, and applied the model to elastic and inelastic scattering by nuclei. [11] We also compared the IA2 effective interaction to the empirical effective interaction (EEI) and the available nonrelativistic theories.

The dominant effect of relativistic density dependence can be described as a short-ranged repulsive contribution to the real central interaction that is proportional to density and nearly independent of energy. This effect is similar to the density dependence of the corresponding component of the empirical effective interaction fitted to data for energy above 300 MeV, but is much stronger than obtained from either the empirical effective interaction or from nonrelativistic nuclear-matter theories for energies below 200 MeV. In addition, Pauli blocking damps the absorptive potential for energies below about 300 MeV; this effect is similar to that obtained from nonrelativistic models.

The density dependence of the IA2 interaction is too strong at low energy to reproduce the inelastic scattering data. Better agreement with the data, and with the EEI, is obtained at 318 MeV. By 500 MeV the IA2 model is in good agreement with the both the data and the EEI, whereas the nonrelativistic theory of the effective interaction fails to predict adequate density dependence. We have also shown that the IA2 models provides excellent predictions for proton absorption and neutron total cross sections.

References

  1. Signatures of density dependence in the two-nucleon effective interaction near 150 MeV, J. Kelly et al., Phys. Rev. Lett. 45, 2012 (1980)
  2. Empirical effective interaction for 135 MeV nucleons, J. J. Kelly, Phys. Rev. C 39, 2120 (1989)
  3. Electroexcitation of isoscalar states in 16O, T. N. Buti et al., Phys. Rev. C 33, 755 (1986)
  4. Empirical effective interaction for 135 MeV nucleons, J. J. Kelly, Phys. Rev. C 39, 2120 (1989)
  5. Effective interactions and nuclear structure using 180 MeV protons. I. 16O(p,p'), J. J. Kelly et al., Phys. Rev. C 41, 2504 (1990)
  6. Effective interactions and nuclear structure using 180 MeV protons. II. 28Si(p,p'), Q. Chen et al., Phys. Rev. C 41, 2514 (1990)
  7. Effective interaction for 16O(p,p') at Ep=318 MeV, J. J. Kelly et al., Phys. Rev. C 43, 1272 (1991)
  8. Empirical density-dependent effective interaction for nucleon-nucleus scattering at 500 MeV, B. S. Flanders et al., Phys. Rev. C 43, 2103 (1991)
  9. Effective interaction for 40Ca(p,p') at Ep=318 MeV, J. J. Kelly et al., Phys. Rev. C 44, 2602 (1991)
  10. Effective interaction for 16O(p,p') and 40Ca(p,p') at Ep=200 MeV, H. Seifert et al., Phys. Rev. 47, 1615 (1993)
  11. Comparison between relativistic and nonrelativistic models of the nucleon-nucleon effective interaction. I. Normal-parity isoscalar transitions, J. J. Kelly and S.J. Wallace, Phys. Rev. C 49, 1315 (1994)

 

Data Tables for Proton-Nucleus Scattering

Extensive data tables for proton elastic and inelastic scattering at intermediate energies are available. Most of these data sets are available using the links tabulated below. For references and additional information, go to Data Tables.

target proton energy (MeV)
9Be 55, 75, 100, 135, 180, 200, 318, 500
16O 100, 135, 180, 200, 318, 500
17O 135
18O 135
28Si 180
30Si 180
32S 318
34S 318
40Ca 100, 200, 318
42Ca 200, 318
44Ca 200, 318
48Ca 100, 200, 318
88Sr 200, 500

Nuclear Structure

Transition charge and current densities can be measured very accurately using electron scattering and compared with models of nuclear structure. I participated in many studies of this type [1-12]. Comparable measurements of neutron transition densities require hadronic probes and careful calibration of the reaction models used to interpret the data. I developed methods for unfolding neutron transition densities from proton scattering data, constructing realistic error envelopes, and testing the accuracy of fitted densities. [13] Data for several different observables and for several different projectile energies can be analyzed simultaneously. I showed that the intrinsic radial sensitivity of intermediate energy protons to the neutron transition density is surprisingly good, and is optimal between about 200 and 500 MeV. Furthermore, I showed that the accuracy of densities unfolded from proton scattering data using the empirical effective interaction is consistent with uncertainty envelopes based upon the statistical uncertainties, penetrability, and range of momentum transfer. Tests include:

Hence, model-dependent errors are now under control. I obtained neutron transition densities for many states among several targets and compared those results with representative models of nuclear structure [14-20]. Contrary to previous practice, it is rarely sufficient to assume that the neutron and proton transition densities have the same shapes; the shape differences often reveal the participation of different orbitals.
 

References

  1. Inelastic electron scattering from 18O, B. E. Norum et al., Phys. Rev. C 25, 1778 (1982)
  2. A test of the interacting boson approximation using electron scattering, F. W. Hersman et al., Phys. Lett. 132B, 47 (1983)
  3. Inelastic electron scattering from 9Be, R. W. Lourie et al., Phys. Rev. C 29, 489 (1983)
  4. Electroexcitation of isoscalar states in 16O, T. N. Buti et al., Phys. Rev. C 33, 755 (1986)
  5. Inelastic electron scattering from collective levels of 154Gd, F. W. Hersman et al., Phys. Rev. C 33, 1905 (1986)
  6. Electroexcitation of M4 transitions in 17O and 18O, D. M. Manley et al., Phys. Rev. C 34, 1214 (1986)
  7. Electroexcitation of 4- states in 16O, C.E. Hyde-Wright et al., Phys. Rev. C 35, 880 (1987)
  8. High-resolution inelastic electron scattering from 17O, D. M. Manley et al., Phys. Rev. C 36, 1700 (1987)
  9. Magnetic Structure of 17O at High Momentum, N. Kalantar-Nayestanaki et al., Phys. Rev. Lett 60, 1707 (1988)
  10. Electroexcitation of rotational bands in 18O, D. M. Manley et al., Phys. Rev. C 41, 448 (1990)
  11. Electron scattering from 9Be, J. P. Glickman et al., Phys. Rev. C 43, 1740 (1991)
  12. Electroexcitation of negative-parity states in 18O, D. M. Manley et al., Phys. Rev. C 43, 2147 (1991)
  13. Intrinsic radial sensitivity of nucleon inelastic scattering, J. J. Kelly, Phys. Rev. C 37, 520 (1988)
  14. Neutron and proton transition densities from 32,34S(p,p') at Ep=318 MeV: I. Isoscalar densities for 32S, J. J. Kelly et al., Phys. Rev. C 44, 1963 (1991)
  15. Neutron transition densities for 48Ca from proton scattering at 200 and 318 MeV, A. E. Feldman et al., Phys. Rev. C 49, 2068 (1994)
  16. Neutron transition density for the lowest 2+ state of 18O, J. Kelly et al., Phys. Lett. 169B, 157 (1986)
  17. Effective interactions and nuclear structure using 180 MeV protons. III. 30Si(p,p'), J. J. Kelly et al., Phys. Rev. C 41, 2525 (1990)
  18. Structure of 9Be from proton scattering at 180 MeV, S. Dixit et al., Phys. Rev. C 43, 1758 (1991)
  19. Neutron and proton transition densities from 32,34S(p,p') at Ep=318 MeV: II.  Neutron densities for 34S, M. A. Khandaker et al., Phys. Rev. C 44, 1978 (1991)
  20. Neutron transition densities from 88Sr(p,p') at Ep=200 MeV, J. J. Kelly et al., Phys. Rev. C 47, 2146 (1993)

 

return to home page