 |
Introductory
Physics: |
 |
 |
Introductory
Physics: |
 |


|
|
Syllabus | Weekly Assignments |
|
and Handouts |
|
|
Instructor: Professor E. Williams (http://www.physics.umd.edu/spg/)
Room 2332 Physics,
Phone 301-405-6156
course web page: http://www.physics.umd.edu/courses/Phys273/williams06/index.html
e-mail: edw@physics.umd.edu (include Phys 273 in subject line -
otherwise e-mail may not be opened)
Office hours: Mon, Tue 1-2 PM (or see me by appointment)
1. Problem sets, 1 set per week, due Thursday at or before the beginning of class.
Typically 6 - 8 problems assigned from the text books.2. On-line "Quizzes", 1 per week. These will be WebAssign problems chosen to encourage study of the basic concepts.
STAPLE your multi-page homework solutions.
3. Exams: October 3, Nov. 7
4. Final Exam: Cumulative examination with an emphasis on material after exam #2.
Monday, December 18, 8:00-10:00 AM
Online "Quizzes" - 10%Regular attendance and class participation is expected, and will serve as a differentiator for borderline grades. Examples and demonstrations presented in class will be included in the material covered by examinations. You should keep a well-organized class notebook and bring it with you when you need to discuss course material with the instructor or TA.
Problem sets: 25%
Exams Exam 1: 20%
Exam 2: 20%
Final: 25%

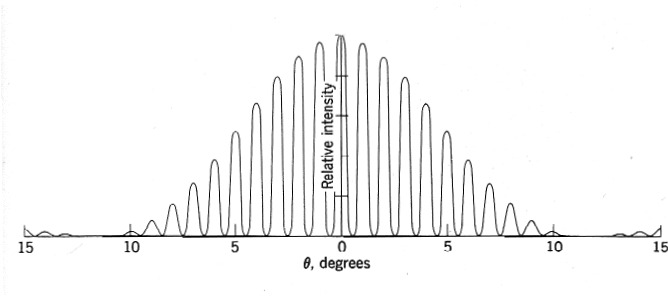
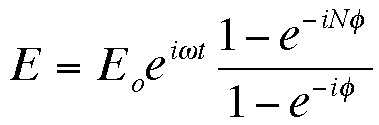 .
.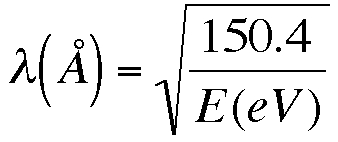 .
. 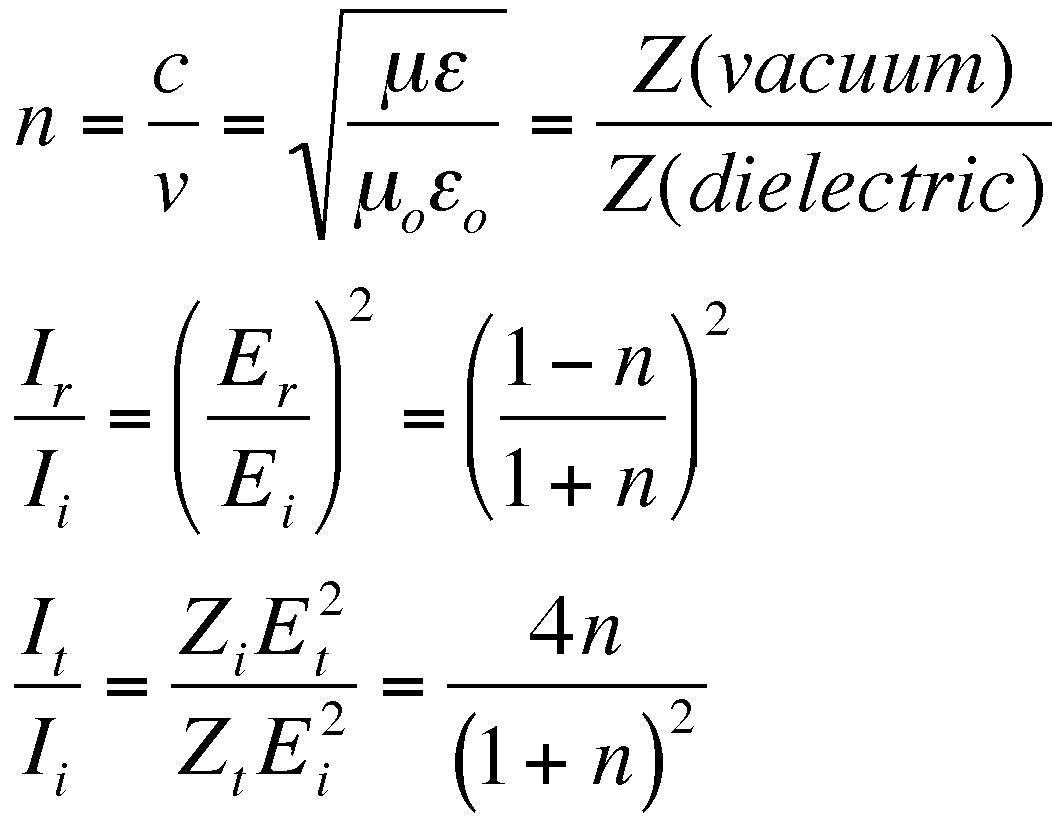
| Copyright
(2006) University of Maryland, College Park. All rights reserved.
Permission to redistribute the contents without alteration is granted to educational institutions for non-profit administrative or educational purposes if proper credit is given to the University of Maryland, College Park as the source. |