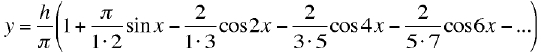|
Physics 273 - Fall 2005
Introductory
Physics:
Waves and Optics
|
 |
.


Course Description
Pre-requisites: Phys 272 (fields) and Math 241 (multivariable
calculus)
Co-requisites: Math 246 or Math 414 (differential eqns)
Content: Oscillations and AC circuits,
Fourier series and integrals, waves on strings, sound; electromagnetic
waves from Maxwell's equations in differential form; physical optics
Phys 273H - To receive honors credit, each student will prepare and
present two class-room demonstrations on topics relevant to the course
material. Description is below.
Syllabus
Physics 273 - Introductory Physics: Waves and Optics
Instructor: Professor E. Williams (http://www.physics.umd.edu/spg/)
Room 2332 Physics,
Phone 301-405-6156
course web page: http://www.physics.umd.edu/courses/Phys273/williams/index.html
e-mail: edw@physics.umd.edu (include Phys 273 in subject line -
otherwise e-mail may not be opened)
Office hours: Tu and Wed, 10-11 AM
Teaching Assistant: Mingdong Li
Room 4219 Physics
e-mail: lmd@umd.edu
Office hours: Wed, 1-3 PM
Class Location:
M Tu W Th 9:00 AM, Room 0405 Physics
Textbooks:
Hirose and Langren, Introduction to Wave Phenomena, Krieger Publishing
2003
ISBN: 1-57524-231-1
Tipler and Mosca, Physics for Scientists and Engineers, 5e,
Vol.
II, W.H. Freeman and Co. 2004.
ISBN: 0-7167-0810-8
Course Outline:
We will be covering material in Ch. 1-14 of Hirose and Langren at
approximately one chapter per week. Not all material in each
chapter will be covered. Material on Fourier techniques in
Chapter 13 will be covered just after chapter 3. Parallel
material from Tipler and Mosca, chapters 29 - 34 will be assigned as
reading and in problem sets.
Evaluations:
1. Problem sets, 1 set per week, due Thursday at or before
the
beginning of class.
Typically 6 - 8 problems assigned
from the text books.
2. Quizzes, 1 per week, normally on Tuesday, 10 minute quiz taken
from pre-assigned example problems in text.
Each quiz will count as two
additional homework
problems on that week's problem set.
3. Exams: October 11, Nov. 15
4. Final Exam: Cumulative examination with an emphasis on
material after exam #2.
The University will
formally assign a date later in the semester. The most likely
time
appears to be
Monday, December 19, 8:00-10:00 AM
Use of a calculator is
allowed and expected on examinations, quizzes and problem sets.
Accommodations for
Students with Disabilities:
The
University has a legal obligation to provide appropriate accommodations
for students with documented disabilities. In order to ascertain
what
accommodations may need to be provided, students with disabilities
should inform me of their needs in the first week of the
semester.
Grading
Problem sets + Quizzes: 25%
Exams: 75% (equal weight for each of the three exams)
Regular attendance and class participation is expected, and will serve
as a differentiator for borderline grades. Examples and
demonstrations presented in class will be included in the material
covered by examinations. You should keep a well-organized class
notebook and bring it with you when you need to discuss course material
with the instructor or TA.
Partial credit will be assigned on problem set and exam problems where
work is clearly presented. A higher standard will be expected for
quiz problems, because you should have prepared by working through the
pre-assigned problems and solutions in advance.
Missed assignments or exams
Late problem sets will not be accepted. The two lowest
problem set scores will be dropped. Quizzes will take place in
the last 15 minutes of class. If you miss the class, you've
missed the quiz. Makeup examinations will only be
given for those with a valid documented excuse (doctor's note, accident
report, certifiable religious observance,
etc.).
If you know ahead of time that you will miss an exam, you must notify
me before the exam. If you miss an exam due to an emergency, let
me know as soon as possible afterwards. I consider requests
for make-ups or any other special consideration to be governed by the
precepts of academic honesty.
Academic Honesty
Working together on assignments is encouraged. However, each
student is expected to do the assigned problems and write the problem
sets independently, and hand in his or her own work for
grading. Examinations and quizzes are closed book and are
expected to be
worked totally independently. For any questions about
academic honesty,
see University policies at:
Assignments
Assignment 11 - Dec. 1-13
Reading:
H&L, Chapter 11, sections 1-7
Tipler Ch. 33, sections 1-4, 6-8
Quiz #11, Thursday Dec. 8
H&L, Ch 11, examples 1, 4 and 5
Tipler, Ch 33, examples 1, 2, 5, 8, 9
Problem Set # 11 (due Tuesday, Dec. 13)
Problems 1-4
(see below)
Problems 5-7 H&L, problems 3, 4, 17
Problems 8- 15 Tipler Ch. 33, problems 18, 20, 26, 34, 42, 50,
58, 72
Problem 1: The amplitude of the electromagnetic field for
the superposition of N coherent electromagnetic waves that differ in
phase by equal multiples of angle φ is: 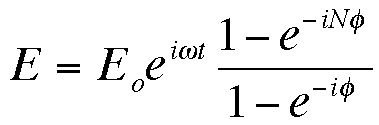 .
.
Find the expressions for the complex conjugate E*, and the intensity of
the superposition I=εcE*E.
Problem 2: How many fringes of yellow-green light (λ =
570 nm) pass a fixed position on the detector of a Michelson
interferometer when one of the mirrors is moved 0.001 mm?
Problem 3: The angle of first order diffraction from a
grating is 15 degrees. In an optics application, the diffraction
beams of a given order act like a set of parallel rays emitted from
different positions on the grating. If the grating is positioned
at s = 20 cm on the optical axis of a converging lens of focal length f
= 12 cm, carefully draw the ray diagram for the first and second order
diffraction beams emitted from two different positions on the
source. Find positions of the 4 beams in the focal plane.
What does your result mean?
Problem 4: An electron has wave-like behavior that allows it
to act like a plane wave of wavelength 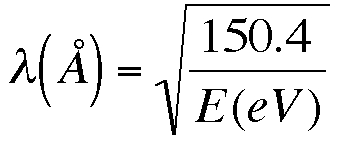 .
.
(An angstrom Å is 0.1 nm.) An electron that scatters off a
crystalline surface gives rise to a diffraction pattern due to
scattering from the periodic array of atoms on the surface. (The
first people to observe and correctly interpret this behavior were
Davisson and Germer; Davisson won the 1937 Physics Nobel prize
for the discovery.) The diffraction angles follow the same
relationship as for a grating (for normal incidence), nλ = dsinθ, where
d is the distance between the atoms.
a) Find the wavelength of electrons accelerated through a
potential of 120V (these electrons have energy 120 eV).
b) Find the angles for first and second order diffraction (n
= ±1, n = ±2) when these electrons are scattered from a
surface where the distance between atoms is 3Å.
Assignment 10 - Nov. 16 - Dec. 1
Reading:
Tipler, Ch. 31, sections 7,8
Tipler, Ch. 32
H&L, Chapter 12, sections 5, 8, 9
Quiz #10 assignment: (quiz on Tuesday, Nov. 29)
H&L, Ch 12, Ex. 7
Tipler, Ch 32, Exs. 2, 4, 8, 9, 11, 16
Problem Set # 10 (due Thursday, Dec. 1)
H&L Ch. 12 # 5, 16, 19
Tipler Ch. 31 # 58, 62
Tipler Ch. 32 # 30, 36, 54, 60, 74, 90, 102, 124
Assignment 9 - Nov. 3 - 10
Reading:
Tipler, Ch. 31, sections 1-6
H&L, Chapter 12, sections 1-2
Quiz #9 assignment: (quiz on Tuesday, Nov. 8)
H&L, Ch 12, Ex. 1 & 2
Tipler, Ch 31, Exs. 3-6
Problem Set # 9 (due Thursday, Nov. 10)
Problems 1-3 (below)
Tipler Ch. 31 #22, 32, 39, 40, 48
Problem 1: The power
output of an antenna of length l, in which there is an oscillating
current of amplitude Io and angular frequency ω is:
P = (lωIo)2/(12εoc3).
Treat the current in the antenna as the load (transmitted) current
provided by a transmission line of impedance Z. If we consider
using a standard cable with Z = 50Ω, what power has to be provided into
the transmission line to create an antenna output of 500 kW at
frequency f = 1.20 MHz?
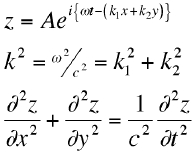
Problem 2: Show that a
transverse wave :
where :
is a solution of the two-dimensional wave equation:
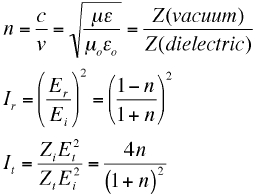
Problem 3: The
relationship between the impedance of a dielectric medium and the
refractive index n is:
Show that when light traveling in free space (refractive index n = 1)
is normally incident on the surface of a dielectric of refractive index
n, the reflected intensity is Ir:
and the transmitted intensity is It:
Assignment 8 - Oct. 27 - Nov. 3
Reading:
Tipler, Ch. 30
H&L, Chapter 9, sections 4-6
Quiz #8 assignment: (quiz on Tuesday, Nov. 1)
H&L, Ch 9, Ex. 7
Tipler, Ch 30, Exs. 3, 4, 6, 7
Problem Set # 8 (due Thursday, Nov. 3)
H&L Ch. 9, Problems 7, 9, 13
Tipler Ch. 30 #11, 16, 31, 44, 46, 56
Assignment 7 - Oct. 20 - 27
Reading:
H&L, Chapter 6
H&L, Chapter 9, sections 1-4
Quiz #7 assignment:
H&L, Ch 9, Exs. 1-4
Problem Set # 7 (due Thursday, October 27)
Problems 1-4
(see below)
Problems 5-10 H&L Ch. 9 #1,2,3,5,6 (postponed to PS #8: Ch. 9, #7)
Problem 1: In class we placed a loud speaker at one end of a
tube with a movable plunger that created a rigid barrier part way down
the tube. We listened to the sound intensity as a function of the
distance of the plunger from the open end of the tube, and found
intensity maxima at 77 cm, 68 cm and 59 cm. What was the
frequency of the sound?
Problem 2: A hanging spring of mass m’, and spring constant s (to
avoid confusion with wave number k) is at a length L when it supports a
mass M. In addition normal harmonic motion, it can support
standing waves with the mass M stationary. The speed of wave
motion on the stretched spring is v2 = sL2/m’.
Assume
that the standing waves have the form:
ξ = (Acoskz +
Bsinkz) sinωt
and use the boundary conditions:
ξ = 0 at z= 0
(z = 0 is the top of the suspended spring)
and
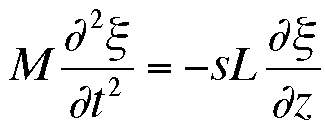
at z = L (the position of mass M at the bottom of the spring),
to find A and B. Use these to show that kLtan(kL) =
m’/M. Then expand tan(kL) in powers of kL to find the second
order approximation that gives ω2 in terms of m’, M and L.
Problem 3: The relationship between the impedance Z and the
refractive index n of a dielectric (like glass) is given by Z =
1/n. Light traveling in free space with a wavelength of 5.5x10-7
m enters a glass lens that has a refractive index of 1.5. Show
that reflections at this wavelength can be avoided by coating the
surface with a material of thickness 1.12x10-7 m and
refractive index 1.22. The refractive index of free space is n =
1.
Problem 4: Find the percentage of energy reflected when a
sound wave in water is normally incident on a planar surface of a)
steel, b) ice, given that
ρc =
1.43x106 kg m-2s-1 for water
3.49 x106 kg m-2s-1
for ice
3.9 x107 kg m-2s-1
for steel
Assignment 6 - Oct. 6 - 20
Reading:
H&L, Chapter 6
H&L, Chapter 7, sections 1-3
H&L, Chapter 8
Quiz #6 assignment (
Tuesday, Oct. 18, students with
conflict due to religious observance
should see me):
H&L, Ch 6, Exs. 1-4; Ch 7,
Ex. 1; Ch. 8, Exs 1,2,3,5
Problem Set # 6 (due Thursday,
October 20
Problems 1-5
(see below)
Problems 6-9 H&L Ch. 6 #1,5,6,8
Problems 10,11 H&L Ch 7 # 1,3
Problems 12,13 H&L Ch 8 # 4,8
Problem 1: The
displacement of a wave on a string which is fixed at both ends is given
by: y(x,t) = Acos(ωt – kx) + rAcos(ωt+kx),
where r is the coefficient of amplitude reflection. Show that
this may be expressed as a sum of two standing waves:
y(x,t) = B(cosωt)(coskx) + C(sinωt)(sinkx), and find expressions for B
and C in terms of A and r.
Problem 2: Standing
acoustic waves are formed in a tube of length l, with a particle
displacement form: ξ(x,t) = (Acoskx+Bsinkx)sinωt. Sketch
the first three harmonics for each of the two cases:
a) Both ends of the tube open, boundary conditions: both
right and left side ∂ξ/∂x = 0
b) Left end of tube open, boundary condition, ∂ξ/∂x = 0; right
end closed, boundary condition ξ = 0.
Problem 3: Show that z =
Aexp(i{ωt - (k1x+k2y)} where k2
= ω2/c2 = k12+k22
is a solution of the two dimensional wave equation:
∂2z/∂x2
+ ∂2z/∂y2 = (1/c2)( ∂2z/∂t2).
Problem 4: An aircraft
flying on a level course transmits a signal of 3x109 Hz,
which is reflected from a distant point ahead on the flight path and
received by the aircraft with a frequency difference of 15 kHz.
What is the aircraft speed?
Problem 5: Show that the Doppler effect when the source and
observer are not moving in the same direction yields:
ν’ = ν c/(c-u’)
; ν’’ = ν (c-v)/c
; ν’’’ = ν (c-v)/(c-u),
if u and v are not the actual velocities, but the components of these
velocities along the direction in which the waves reach the
observer.
Here ν’, ν’’ and ν’’’ represent respectively the cases of moving
source, moving observer and both source & observer moving; with u =
source velocity and v = observer velocity.
Assignment 5 - Sept. 29 - Oct. 6
Reading:
H&L, Chapter 13, section 3
H&L, Chapter 5
Quiz #5 assignment: (quiz
Tuesday Oct. 4, students with conflict due to religious observance
should see me)
H&L, Ch 13, Ex 3; Ch 5, Exs 1, 2, 4, 6
Problem Set # 5 (due Thursday, October 6
Problems 1-3 (see below)
Problems 4-5 H&L Ch. 13 #2, 3
Problems 6-10 H&L Ch 5 # 4, 6, 9, 11
Problem 1: A half-wave rectifier removes the negative half-cycles
of a pure sinusoidal wave, y = hsin(x). Show that the Fourier
series is given by:
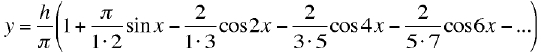
Problem 2: Sound transmission in a gas:
a) Show that in an ideal gas at temperature T, the average
thermal velocity of a molecule is approximately equal to the velocity
of sound.
b) If the velocity of sound in air (density 1.29 kg/cubic meter)
is 330 m/s, find the acoustic pressure for the painful sound intensity
of 10 W/square meter.
c) Find the displacement amplitude of an air molecule at the
painful sound level of 10 W/square meter at 500 Hz.
d) Find the displacement amplitude of an air molecule at the
barely audible level of 10-12 W/square meter at 500 Hz.
Problem 3: A thin rod of copper has a Young’s modulus of 12.4x1010
Pa. A copper rod is given a sharp compressional blow at one
end. The sound of the blow, traveling through air at 0 degrees
centigrade, reaches the opposite end of the rod 6.4 ms later than the
sound transmitted through the rod. What is the length of the
rod?
Assignment 4 - Sept. 23 - 29
Reading: H&L, Chapter 4, sections
1-4, 6
H&L, Chapter 7, section 4
H&L, Chapter 13, section 3
Quiz # 5 problems (quiz will be one of these):
Ch 4, Ex 1, 2, 5; Ch 7, Ex 2; Ch 13, Ex 3
Problem Set # 4 (due Thursday,
September 29)
Ch 4, # 5, 6, 9, 10, 13 (omit momentum part of question on
# 6)
Ch 7, # 4
Postponed: these will be
assigned on PS # 5 - Ch 13, # 2, 3
Assignment 3 - Sept. 15 - 22
Reading:
H&L, Chapter 2, sections 5-7
H&L, Chapter 3
H&L, Chapter 13, sections 1 & 2
Quiz #4 problems (quiz will be one of these):
H&L, Ch 2, examples 5&6, problem 10 (p. 48-9), problem 11 (p.
49)
Problem Set # 3 (due Thursday, September 22
Problems 1-3 (see below)
Problems 4-5 H&L Ch. 2 #9, 12
Problems 6-9 H&L Ch 3 # 4, 5, 7
Problem 1: Prove that the slope of a string at any point x
is numerically equal to the ratio of the particle speed (vertical
displacement speed) to the wave speed at that point.
Problem 2: A transverse sinusoidal wave is generated at one
end of a long horizontal string by a bar which moves the end up and
down through a distance of 0.50 cm. The motion is continuous and
is repeated regularly 120 times per second. The string has a
linear density of 0.25kg/m and is kept under a tension of 90 N.
a) Find the wave speed, amplitude, frequency and wavelength of
the wave motion.
b) Find the velocity and acceleration of the string at a point 62
cm from the generating point. Assume that at y(0,0) = 0.
c) Find the maximum value of the vertical displacement speed and
the maximum value of the vertical component of the (left-to-right)
force acting on the string. At what value of the phase, kx-ωt, do
the maxima occur?
d) What is the maximum power transferred along the string, and
what is the string displacement where the maximum power occurs?
c) What is the minimum power transferred along the string, and
what is the string displacement where the minimum power occurs?
Problem 3: A mathematically pure A-major chord consists of A
at 440 Hz, C# at 550Hz and E at 660 Hz.
a) Calculate and plot the displacement vs. time for the
superposition of three waves of these frequencies, assuming all are
present at the same amplitude.
b) An AM radio station broadcasting at 600 kHz leaves its
transmitter running, broadcasting a steady A-major chord. Sketch
the output signal (vs. time) and calculate the frequencies present in
the signal.
Assignment 2 - Sept. 8 - 15
Reading: H&L Chapter 1,
section 7
T&M Chapter 29 section 6
H&L Chapter 2, sections 1-4
H&L Chapter 3
Quiz : Tuesday Sept. 13, Problem will be one of:
Tipler Example 29-5
H&L
Chapter 2, example problems 1, 2, 3,
H&L
Chapter 3, example problems 1, 2
Problem Set #2
Due: Thursday, September 15 in class
Problem 1: Tipler Ch. 29 # 82
Problems 2-5 H&L Ch 2, # 3, 4, 7, 8
Problems 6-7 H&L Ch 3, # 2, 6
Assignment 1 - Aug. 31- Sept. 8
Reading: H&S Chapter 1, T&M Chapter 29 sections 3,
5 and 6.
Quiz #1: Thursday Sept. 1, Problem will be one of:
H&L Chapter 1, example problem 2 (p. 6) or problem 5 (p. 22).
Quiz #2: Wednesday, Sept. 7, Problem will be one of:
H&L Ch. 1 # 11
Tipler Ch. 29 Example 29-2 (figure 29-6)
Tipler Ch. 29 Example 29-3 (figure 29-8)
Tipler Ch. 29 Example 29-4 (figure 29-12)
Problem Set #1
Due: Thursday, September 8 in class
Problem # 1: Derive the values of beta and omega-prime for a
damped harmonic oscillator as discussed in class in terms of the
physical parameters k (the spring constant) and b (the damping
constant).
Problems 2 - 4: H&L Ch.1 # 2, 10, 16
Problems 5 - 6: Tipler Ch. 29 # 35, 42
Classroom Demonstrations
I will occasionally use classroom demonstrations to illustrate ideas in
the course. You should not treat these demonstrations as
opportunities for a nap - the material presented will be included in
the
material covered on examinations. The demonstrations will be
listed below as they are presented.
September 1: Mass on a
spring with damped harmonic motion measured using a sonar ranger.
The envelope of the decay curve can be used to extract information
about the damping coefficient. Think about how that can be
quantified.
September 7: Eddy Current
Pendulum - wood vs copper pendulum swinging between the poles of a
strong magnet. The damping of the copper pendulum is due to
induced current and generation of magnetic field. Think
about energy storage and applications.
September 13: Coupled
Harmonic Oscillators - two frequencies corresponding to in phase and
out-of-phase oscillation, and display of displacement vs time and
Fourier transform spectrum (amplitude spectrum) (Imran Shamim)
September 19: Wave driven
ratchet to lift a mass
Tuning bars with a small mass attached to one to change the frequency
slightly
September 20: Beaker
breaker - a sound wave is tuned in frequency to match the resonance
frequency of a beaker. When the volume (wave intensity) of the
sound is increased, the beaker shatters.
September 26:
Longitudinal wave illustration on a slinky
September 28: Synthesis
of Wave shapes and Carrier modulation with complex wave shapes,
with Fourier spectrum analysis (Ari Halper-Stromberg)
October 3: Bell in
vacuum, Wave forms displayed on oscilloscope and simultaneously
played on speaker
October 5: Speaker and
candle: physical displacement of speaker generates air currents
that displace flame
October 6: Doppler
effect: Whistling ball twirled overhead creates audible shifts in
frequency. Display of frequency spectrum vs. time shows the
values of the shift quantitatively and allow the speed to be
determined. (Siwei Kwok)
October 11: Resonance
Tube - oscillator and plunger. A speaker is set up at one end of
a plastic tube, and a movable plunger sets a solid reflecting wall at
the other end of the tube. As the plunger is moved back and
forth, the volume of the sound increases and decreases.
October 11 and 18: Shive
Machine - a parallel series of sticks mounted on a torsional wire
illustrate wave motion. Reflections at a fixed and a free end,
and transmisssion into a second shive series with sticks of different
lengths are shown. Standing waves can be set up by controlling
the driving frequency.
October 19: Two speakers
both projecting the same bass signal. Projection of sound in
three dimensional path. Reversal of phase of one speaker
dramatically decreases the intensity of the bass (low frequency)
sound. Concept of constructive interference vs. destructive
interference.
October 24: A voltage
pulse generator is used to create a pulse on a coaxial cable
(transmission line). The reflected pulse is detected a time
later, and given the known (for that cable) wave speed, the length of
the cable is determined. Then a second cable of different
impedance is connected and reflections from the junction and the
termination are determined, and their amplitudes and phases are
compared with predictions. (Samuel Pinkava)
November 3: Light bulb
and radiometer with ruler - we measured intensity as a function of
separation distance between the bulb and the radiometer.
November 8:
Refraction: laser light into water, visual appearence of a rod
half-immersed in water. Total internal reflection: laser
light in falling stream of water and in a curved thin film.
November 9:
Refraction: laser light incident horizontally into a tank of
water bends downward due to ??
November 17: 1)
Refracted
images of can at corner of tank of water (Imran Shamim). 2)
Light
and two polarizers - rotate second to demonstrate Malus' law.
Insert a third polarizer between the original two polarizers.
3) Special quarter wave plate inserted at 45 degrees between
two polarizers.
December 1: Focusing of
parallel rays with spherical and hyperbolic lenses. String
models of spherical and chromatic aberrations. Repeat of November
17 polarization demos. Three-filter Malus' law demo.
Creation of circularly polarized light with birefringent quarter-wave
plate.
December 6: Michelson
interferometer. a) laser source, relating the number
of times an intensity minimum (fringe) passes to the wavelength of the
laser source and the mirror diplacement. b) white
light source, relating the number of times the color oscillates through
the spectrum to the wavelength and mirror displacement. (Samuel
Pinkava)
December 12: Laser light
source and slits of variable number, spacing and width (Ari
Halper-Stromberg)
December 13: Water prism
(Siwei Kwok)
Solution Sets and Handouts
these are downloadable files
or web links
Fourier Synthesis:
Go to the bottom of the page, enter a number in the “harmonics” box and
select the “enter data” button, a window will open in which you can
enter amplitudes and phases. The simplest addition has all
amplitudes = 1 and all phases = 0. Try it for increasing numbers
of harmonics. These sums are limited to waves with frequency
equal to multiples of a fixed base frequency.
Fourier Series:
Handout-sum of incident and reflected
waves (total reflection)
Handout - sum of incident wave
and partially reflected wave
some
group velocity wave demonstrations
a
nice set of animations of reflections
a nice standing wave animation
<>
http://en.wikipedia.org/wiki/Standing_wave
great quick time movies of EM wave
behavior
Java applet of Brewster's angle.
Note the incident wave is shown as the combination of two orthogonal
electric fields (magnetic fields not shown). Be sure to use the
view angle knob to get the full impact of the animation.
Handout- Table of impedances, etc. for
different wave types
Handout - Notes on Michelson
inteferometer
Handout - Notes on Birefringent
quarter wave plate
Handout- Williams solutions for
Tipler Ch 32 # 74 and 102
 Physics 273H
Honors Option
Physics 273H
Honors Option
To receive honors credit, each student
will prepare and present two classroom demonstration on topics relevant
to the course material. Presentations will graded and will
count for 10% of the total course grade. The remaining 90% will
be determined by the normal 273 material.
Demonstrations can be based on the equipment and previously-developed
demonstrations available in the Physics Department
lecture-demonstration facility:
http://www.physics.umd.edu/deptinfo/facilities/lecdem/services/demos/mainindex.htm
Students should discuss their ideas with me, and I will give feedback
and help with accessing the necessary equipment and developing the
demonstration. Each student must schedule one of the two demonstrations
before Oct. 6. Demonstrations must be scheduled in advance to
match the course material. No more than two demonstrations will
be scheduled in any one week.
Presentations:
Presentations should be approximately 10 minutes in length. They
should include 1) an introduction of the subject in the context
of the course material, 2) a physical demonstration illustrating
in a clear and compelling fashion a well-defined physical effect, and
3) a brief presentation of a quantitative analysis of the
observations.
The presentations will be evaluated using the following criteria:
1) Level, organization and correctness of material
presented 30%
2) Effectiveness of the demonstration
40%
a) illustrating phenomenon of interest
b) allowing quantitative analysis –
3) Quality of the presentation –
30%
e.g. does it hold class interest, can
others take the information presented and use it effectively
Potentially useful demonstrations:
Some lecture demonstrations (see web page above) that have useful
equipment and ideas that can be modified for a presentation for the
material in the first 1/2 of the semester include:
G1-37 (data acquisition system includes fourier analyzer)
G2-26, G3-26 (different combinations of mass/spring possible, can
couple with motion sensor)
G3-44
G4-41
H2-01, H2-28
H3-01, H3-02
H4-01, H4-02, H4-04, H4-52 (not shown on pages, but useful for good
demos is fourier analyzer)
Some lecture demonstrations useful for the material in the second 1/2
of the semester include:
G4-41 Solitons
H1-27 Lissajous figures for sound
K8-04, K8-32 EM wave speed in transmission line, air,
dielectric
K8-11, 13 EM standing waves
K8-42 Radiowave dipole pattern
L1-31 Laser cavity
L4-41, L4-04, L6-07,09 Microwave refraction
M1-01, 02, 03, 04, 11, 21, 22, M2-01 Laser Diffraction
M3-01, 04 Interferometer
M3-21, Microwave interferometry
M3-41 Fabry Perot interferometer
Copyright
(2005) University of Maryland, College Park. All rights reserved.
Permission
to redistribute the contents without alteration is granted to
educational
institutions for non-profit administrative
or
educational purposes if proper credit is given to
the
University of Maryland, College Park as the source. |






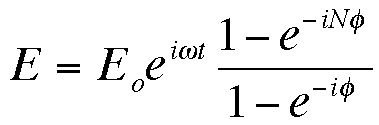 .
.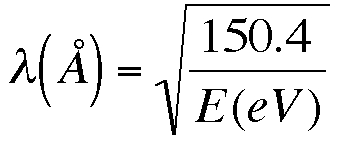 .
. 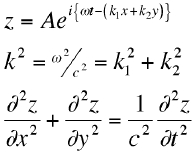
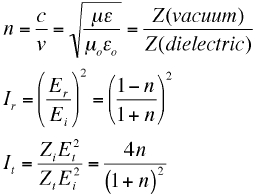
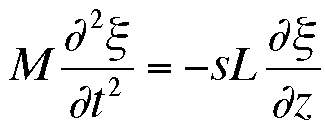 at z = L (the position of mass M at the bottom of the spring),
at z = L (the position of mass M at the bottom of the spring),