Heavy electrons: new ways to break old rules
By: Johnpierre Paglione

In 1853, well before the discovery of the electron by J. J. Thomson in 1897, two German physicists named Gustav Wiedemann and Rudolf Franz made the peculiar observation that the ratio of electrical to thermal conductivities is the same in several different metals. Although not as famous as the discovery of superconductivity in mercury by Kamerlingh Onnes over fifty years afterward in 1911, this experiment marked one of the first quantitative studies of the inner nature of metals and would turn out to play a pivotal role in guiding the development of the quantum theory of solids. Much effort went into explaining “the law of Wiedemann and Franz”, with the first successful (although fortuitousⁱ) theoretical explanation given by Drude in 1900 in terms of a classical gas of electrons. The advent of quantum mechanics played a crucial role in advancing this interpretation, leading to corrections by Sommerfeld and Bloch in 1928 employing the concept of a Fermi gas of particles that obey quantum mechanical statistics.

	Apparatus used by Wiedemann and Franz in 1853 to compare the electrical and thermal conductivities of several metals.

While the non-interacting quantum gas picture was quite successful, it was still not obvious how the interactions between ~10²³ electrons confined within a small chunk of metal could be completely negligible. This remained a mystery for some time, but the last piece of the puzzle, called Fermi liquid theory, was provided by L. D. Landau in 1957. This theory presented a new way of thinking about the strong interactions present in a system, introducing the notion of “dressed” electrons, or so-called “quasiparticles,” that can be treated as non-interacting particles with the same quantum variables as bare electrons, but with the effects of their interactions buried within renormalized quantities such as their mass. This finally explained the law of Wiedemann and Franz as a simple consequence of having spin ½, charge ‘e’ fermionic particle excitations that transport a set ratio of heat and charge quantities given only by fundamental constants.


In 1975, Fermi liquid theory was put to the test with the discovery of a new class of metals which pushed the quasiparticle idea to the extreme: CeAl₃, the first reported “heavy-fermion” system, is one of several metals which harbor quasiparticles with effective masses approaching 1000 times that of the bare electron mass. And yet, these are well described by Landau’s theory; considering this means electrons in these materials are slowed down to the speed of sound, this is truly amazing!  However, the world is not so simple – many other materials exhibit strange metallic properties that do not fit Landau’s picture, and for lack of a better term are often branded as “non-Fermi liquids.” For example, some heavy-fermion systems on the verge of magnetism can be experimentally tuned by applying external pressures or strong magnetic fields to traverse through a zero-temperature phase transition between two stable ground states. Because it occurs at absolute zero temperature, the character of such a “quantum critical point” is dictated by quantum effects rather than the thermal fluctuations that dominate normal phase transitions. More important, the influence of these quantum fluctuations can disrupt the formation of long-lived quasiparticles down to the lowest measured temperatures, some 10,000 degrees below where that occurs (i.e. the Fermi energy) in normal metals, causing electronic masses to appear to diverge toward infinity.

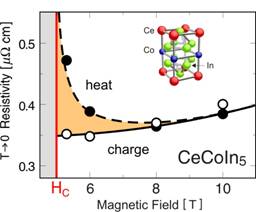
	Comparison of heat and charge conductivities at absolute zero temperature in the heavy-fermion material CeCoIn5.

The question is, are these quantum fluctuations simply altering the behavior of quasiparticles in an as-yet misunderstood manner, or have we finally gone well beyond the limits of Landau’s theory? Cut to the law of Wiedemann and Franz: this nice, simple description of spin ½ charge e particles carrying a fixed ratio of heat and charge actually has profound implications. It turns out to be very difficult, so far impossibly soⁱⁱ, to break this relation if you start with Landau’s quasiparticles as an ingredient; being individual entities, they simply carry heat as well as charge. In this light, an experimentally observed violation of this law is considered “smoking gun” evidence for the failure of Fermi liquid theory. Recently, studies of the low-temperature heat and charge conductivities of the heavy-fermion material CeCoIn₅ [Tanatar et al., Science 316, 1320 (2007)] have unearthed a violation of the Wiedemann-Franz law as the temperature of the system approaches absolute zero and the ground state is tuned to a quantum critical point. By turning a knob on the magnet power supply, this system can be tuned back and forth between a Fermi liquid ground state, where quasiparticles are well behaved and the Wiedemann-Franz law is obeyed, and a strange metallic state where the WF law does not hold, suggesting that the quasiparticle description has met its match.


Does this behavior mark the death of the quasiparticle and the demise of the Fermi liquid? Oddly, yes and no. It appears that Nature simply refuses to completely abandon Landau’s picture: even when tuned directly to the critical magnetic field, the observed violation in CeCoIn₅ only thrives when heat and charge currents are applied along one particular direction of the tetragonal crystalline lattice, and not the other. In other words, it is only under the most stringent conditions that the Wiedemann-Franz law can be forced to break down, making it no surprise that this law has stood for so long. While Gustav and Rudolf may be dismayed to know their law has finally been broken, they would surely be impressed to know that it has been the law of the land for over 150 years. Now that’s an experiment to remember.

------------------------------------------------------------------------------------------------------------------------------------------------------
Johnpierre Paglione is an Assistant Professor in our Condensed Matter Research Group. For questions or comments, he can be reached at paglione@umd.edu