| (1) |
| (4) |
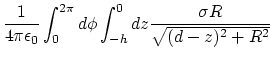 |
|||
![$\displaystyle {Q\over 4\pi \epsilon_0 h } \ln \left[ { \sqrt{ d^2+R^2} -d \over
\sqrt{(d+h)^2 +R^2} -(d+h)} \right]~,$](img44.gif) |
(5) |
using the integral formula
The electric field is in the direction of the axis of the cylinder from
the azimuthal symmetry, so
![]() , which gives
, which gives
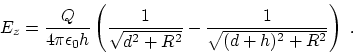 |
(6) |
(a) Within the pipe,
![]() . Here one simplification we can
make is to drop the
. Here one simplification we can
make is to drop the ![]() dependence since the system is translationally
invariant in
dependence since the system is translationally
invariant in ![]() . So the equation reduces to
. So the equation reduces to
![]() .
.
Using the separation of variables technique in Cartesian coordinates
(because the system is rectangular),
where
since the function is expected to be periodic in
The solution is obtained as
and
. From the boundary conditions
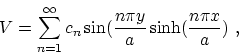
where
We can determine the coefficients ![]() from the remaining boundary
condition at
from the remaining boundary
condition at ![]() ,
,
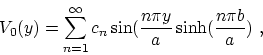
which leads to
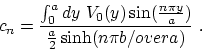
(b) You simply replace ![]() , which gives
, which gives
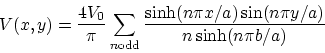
where
(B) Electric field: Since
![]() for a linear dielectric,
for a linear dielectric,
| (8) | |||
| (9) |
(C) Electric potential: The potential can be obtained from integrating
the electric field from infinity as follows
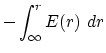 |
(10) | ||
| (11) | |||
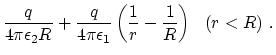 |
(12) |
(D) Bound surface charge: It is the bound surface charge that makes
the electric field discontinuous upon crossing the surface of the
sphere at ![]() . In other words,
. In other words,
![]() for
for
![]() . The result from (B) above
can be used to calculate the following:
. The result from (B) above
can be used to calculate the following:
| (13) |
Next: Midterm 2 Up: Midterm 1 Previous: Questions Hyok-Jon Kwon
2001-12-19