Problems for
Intermediate Methods in Theoretical Physics

Edward F. Redish

Using de Moivre's Theorem

Use the complex exponential method to express sin(nθ) and cos(nθ) as functions of sin(θ) and cos(θ) for n = 2, 3, and 4. (The results for n = 2 are shown on the page "Applications of the Complex Exponential and De Moivre's Theorem."

Solution

The trick here is to express the exponential of i times 2θ in two ways: as itself and as the square of i the exponential of i times θ. We then expand using deMoivre's theorem on both sides and just expand out the square. Here's how it works.

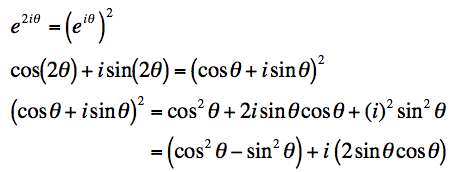
We now equate the real and imaginary parts and get our result.

.

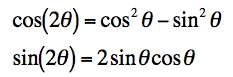It's a bit more complicated for the cube since we need to expand a cube. Remember this is how it works (see a reference to Pascal's triangle):

When we do this with the complex exponential, here's what we get:

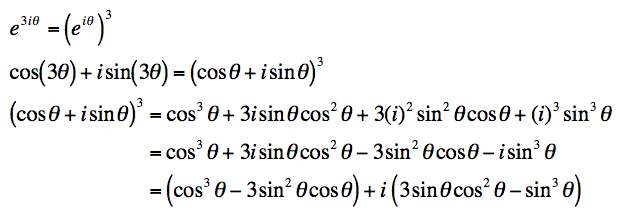
Here, we had to note that i2 = -1 and i3 = -1. The result is:

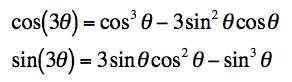
For the fourth power, it's even messier. Here we have to note that i4 = 1.

.

RETURNS

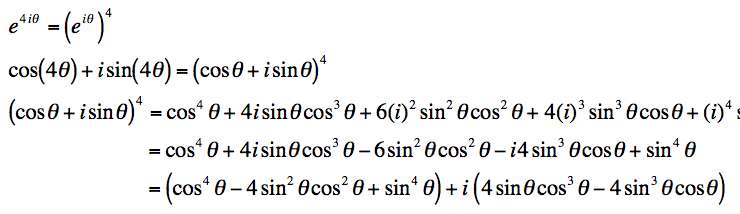
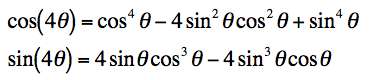
University of MarylandPhysics DepartmentPhysics 374 Home

This page prepared by

Edward F. Redish
Department of Physics
University of Maryland
College Park, MD 20742
Phone: (301) 405-6120
Email: redish@umd.edu

Last revision 16. October, 2005.