Complex Numbers

Applications of the Complex Exponential and De Moivre's Theorem

easily and directly gives a lot of nice and rather remarkable results. Here are two examples:

.

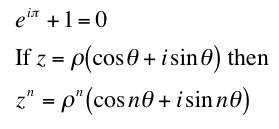The first of these is called Euler's theorem. It combines e, i, π, 1, and 0. Many consider this the most elegant of all mathematical equations. The second is called de Moivre's theorem. If you raise the polar form of z to some power and equate it to the de Moivre form, you can easily get expressions for cos nθ and sin nθ in terms of cos θ and sin θ.

For example:

.

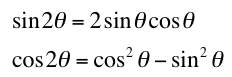Equating the real part on the left to the real part on the right and the imaginary part on the left to the imaginary part on the right gives the well-known (but otherwise cumbersome to prove) results:

.

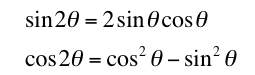If you try to prove these using trig identities you will see how much work de Moivre saves us!

Exercise: Use de Moivre's theorem to figure out what cos 3θ and sin 3θ are in terms of sin θ and cos θ.

RETURNS

University of Maryland	Physics Department	Physics 374 Home