6) Energy conservation is sometimes a useful principle in helping us
solve problems concerning the motion of objects. Suppose a single object
is moving subject to a number of forces. Describe how you would know whether
energy conservation would hold for the given example and in what kinds
of problems you might find it appropriate to use it.
7) A professor of physics is going ice skating for the first time. He
has gotten himself into the middle of an ice rink and cannot figure out
how to make the skates work. Every motion he makes simply slips on the
ice and leaves him in the same place he started. He decides that he can
get off the ice by throwing his gloves in the opposite direction.
(a) Suppose he has a mass M and his gloves have a mass m. If he throws
them as hard as he can away from him, and they leave his hand with a velocity
v. Explain whether or not he will move. If he does move, calculate
his velocity, V.
(b) Discuss his motion from the point of view of the forces acting on him.
(c) If the ice rink is 10 m in diameter and the skater starts in the center,
estimate how long it will take him to reach the edge, assuming there is
no friction at all.
8) A child's game consists of a block that attaches to a table with
a suction cup, a spring connected to that block, a ball, and a launching
ramp. By compressing the spring, the child can launch the ball up the ramp.
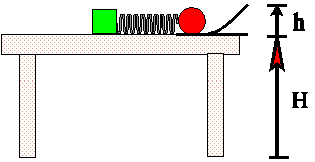
The spring has a spring constant k, the ball has a mass m,
and the ramp rises a height h. The spring is compressed a distance
s in order to launch the ball. When the ball leaves the launching
ramp its velocity makes an angle q with
respect to the horizontal.
(a) Assuming that friction and air resistance can be ignored for the
purposes of this problem, describe the changes in the forms of energy in
the system from the time the spring is compressed until the ball first
hits the ground.
(b) Calculate the vector velocity of the ball when it leaves the launching
ramp. Be sure to specify your coordinate system.
(c) The spring constant = 32 N/m, the spring's compression is 5 cm, the
ball's mass is 20 grams, the height of the ramp is 10 cm, and the top of
the table is 1 m above the floor. With what speed will the ball hit the
floor? (Use g » 10 m/s2.)
9) Two identical carts of mass m are sliding on an air track. Cart 1
approaches cart 2 with velocity V1. Cart 2 is at rest. Cart
1 has a spring on its leading edge. The spring has a spring constant k
and is held compressed a distance c by a latch. When cart 1 touches cart
2, the latch is released and all the spring's energy is given to the motion
of the two carts. Ignore frictional losses in the spring and to the track.
(a) You want to find the velocities of the two carts after the collision,
V1' and V2'. Write two equations which will let you
do this and state why you can use them here.
(b) Solve your equations for V1' and V2'. If you
find two solutions, discuss which of your solutions you want to use. (Hint:
Consider the case when the spring constant goes to 0.) Does the second
cart move faster or slower than it would if there were no spring?
10) Construct the Newton drag law for air resistance by filling in the
equations that go with the following arguments. Assume a sphere of radius
R is moving with velocity v through a dense crowd of tiny particles, of
number density n per cm2, with each
having mass m.
(a) Assume in a small time Dt that the sphere's
velocity doesn't change. What volume of air does it move through and how
many particles get swept away in the time Dt?
(b) Assume that each particle "swept away" has its velocity changed
from 0 to 2v. What is the total momentum, Dp,
added to the air molecules by being "swept away" by the sphere
in the time interval Dt?
(c) If the particle hits the molecules and changes their momentum by Dp,
it must exert a force on them. By N III, the molecules must also exert
a force back on the ball. Use the impulse-momentum theorem to calculate
the force on the ball exerted by the air molecules.
(d) Compare your result to the one derived in class and show it has the
form |F| = hrR2 v2. What
value of h do you get?
11) When objects are too small to be seen by a microscope, physicists
often probe them by shooting microscopic particles from the objects and
observing how the particles scatter. (R. P. Feynman once described this
process as "trying to find out the shape of a wineglass by shooting
buckshot at it"!) The M.U.P.P.E.T. program SCATTER
* simulates a simple model for this process.
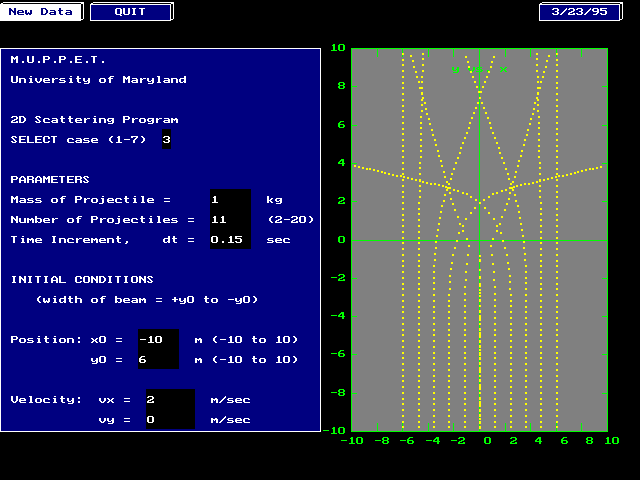
The program models shooting a beam of classical particles at a force
field in two dimensions. (The best way to think about this is to imagine
rolling a bunch of marbles or ball bearings along the ground and trying
to use their paths as seen from above to determine the shape of hills and
valleys in the ground they move over. The height of the ground corresponds
to the potential energy of the force field.) A typical screen is shown
below. The particles start at the bottom of the graph and move upward.
The picture shown has a beam of 5 particles all travelling parallel toward
the top of the graph at a speed of 2 m/s. You can change the number of
particles, the width of the beam (by changing y0), and the speed.
The trajectory of each particle is laid down as dots, one place every
0.15 second. (You can change this by changing dt.) When the dots are close
together the particle is moving slowly. When they are far apart, the particle
is moving fast.
There are 7 different force fields that you may probe. Choose one, find
out all you can about it and write up your results. You may give information
about the force as a function of position or about the potential energy
as a function of position. You may use energy conservation, momentum conservation,
or whatever else you like. You may print out the screen and measure the
change in spacing of the dots to get the acceleration.
12) An electron at rest has an angular momentum equal to h/4p,
where h = Planck's constant (6.63 x 10-34 J-s). At one time
it was suggested that the electron was a uniform sphere with radius equal
to about 2 x 10-15 m. (This value is obtained by setting the
electrostatic potential energy of a uniform sphere of charge equal to mc2.
Suppose this were so, and the angular momentum arose from the sphere's
rotating with an angular velocity w
(a) Find the value of w required to get the
necessary angular momentum.
(b) Calculate the speed with which the electron's equator would be rotating.
(Your answer should come out greater than the speed of light. Rumor has
it that in the 1920's one student was discouraged from publishing his idea
that the electron had a spin by Wolfgang Pauli presenting him with this
calculation. The result is wrong for two reasons. First, if the electron
were a sphere spinning that fast, one would have to take relativity into
account. The classical formula for angular momentum wouldn't hold. Second,
as far as we know, the electron isn't a sphere but is about as close as
we can get to a true point. It has built in angular momentum anyhow --
but not from spinning!)
13) An oxygen molecule of mass M is sitting at rest minding its own
business. Suddenly, a cosmic ray photon passes by and adds an energy D
to the molecule. The molecule sits and wiggles for a while, and the breaks
up into two equal mass oxygen atoms traveling in opposite directions.
(a) How fast is each oxygen atom traveling?
(b) Suppose the process took place while the oxygen molecule was traveling
with a velocity V and the atoms went out after the breakup in the
same direction as V. What velocities would they have viewed from
this frame?
14) (a) Describe how a solid ball can move so that (i) its total kinetic
energy is just the energy of motion of its center of mass, and (ii) its
total kinetic energy is the energy of its motion relative to its center
of mass.
(b) Two bowling balls are moving down a bowling alley so that their centers
of mass have the same velocity, but one just slides down the alley, while
the other rolls down the alley. Which ball has more energy? Explain.
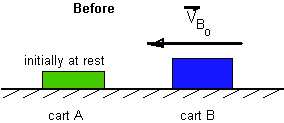
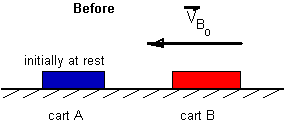
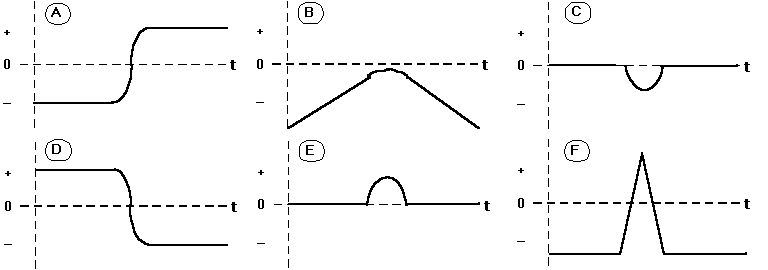
| 15) Two carts are riding on an air track as shown in the figure at
the right. At clock time t = 0 cart B is at the origin traveling in the
+x direction with a velocity speed vB0. At that time, cart A
is at the position shown and is at rest. Cart B has twice the mass of cart
A. The carts "bump" each other, but don't stick. |
|
In the graphs below are shown a number of possible plots for the various
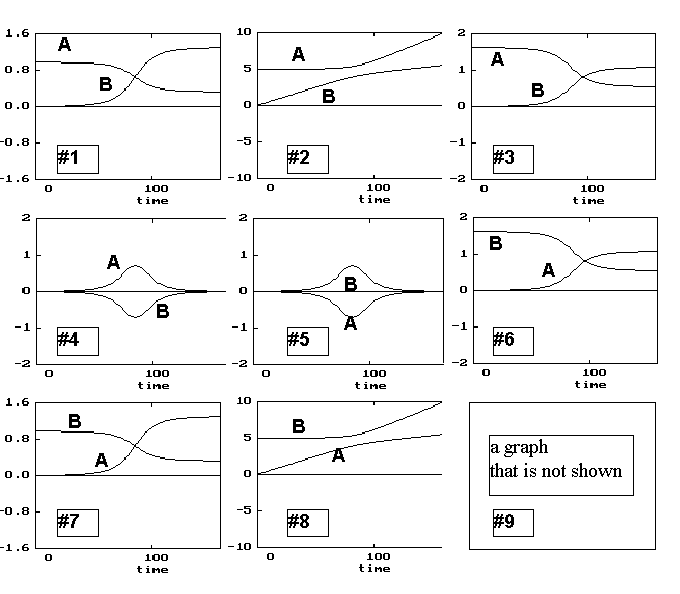
physical parameters associated with the two carts. Each graph has two curves,
one for each cart and labeled with the cart's letter. For each property
(a)-(e) select the letter of the graph that could be a plot of the property.
(a) The force exerted by the carts.
(b) The position of the carts
(c) The velocity of the carts
(d) The acceleration of the carts
(e) The momentum of the carts.
16) Can a system whose momentum is conserved be made up of smaller systems
whose individual momenta are not conserved? Explain why or why not and
give an example.
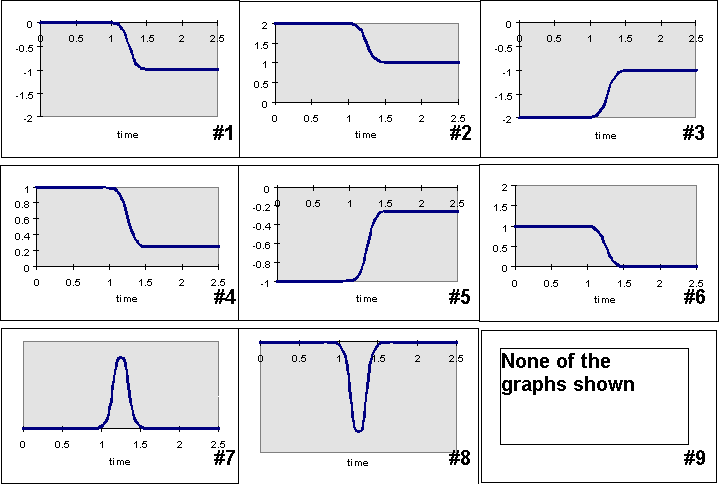
17) In the figure below are shown two carts on an air track. The carts
have equal masses. At the time shown, cart B is moving in the negative
x direction and the center of mass of cart A is at the origin and at rest.
When the carts collide, they stick together. Friction with the track is
small and may be neglected
In the graphs below are shown a number of possible plots for the various
physical parameters associated with one of the two carts. For each property
(a)-(e) select the number of the graph that could be a plot of the property
as a function of time.
(a) the momentum of cart A
(b) the kinetic energy of cart B
(c) the position of (the center of mass) of cart B
(d) the acceleration of cart A
(e) the total momentum of carts A+B
18) Energy conservation is sometimes a useful principle in helping us
solve problems concerning the motion of objects. Suppose a single object
is moving subject to a number of forces. Describing how you would know
whether energy conservation would hold for the given example and in what
kinds of problems you might find it appropriate to use it.
19) Is it possible for a system of interacting objects to conserve momentum
but not mechanical energy (kinetic + potential)? Discuss and defend your
answer, then given an example that illustrates the case you are trying
to make.
| 20) A block, of mass M = 0.50 kg, rests on a frictionless horizontal
table so that it is in contact with a spring of negligible mass and spring
constant k = 600 N/m. A toy dart, of mass m = 0.10 kg, is shot at
the block with a speed vi = 15 m/s (as is shown in part
(a) of the figure). The dart sticks to the block with a suction cup. As
a result of the impact, the spring first compresses (as shown in part (b)
of the figure). After the spring has returned to its equilibrium position,
the block and dart move away from the spring, traveling to the left with
a speed vf along the table (as shown in part (c) of the
figure).
(a) What is the change of length of the spring as it is compressed from
its initial length to its length at maximum compression?
(b) At the instant when the block is momentarily at rest and the spring
is at its maximum compression, is the acceleration of the block zero, directed
to the right, or directed to the left? Explain why.
(c) What is the final speed vf of the block and attached
dart?
From the book of Fred Reif.
|
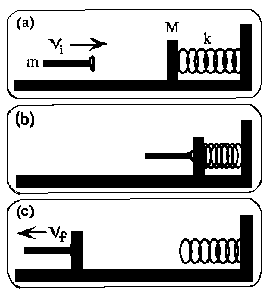 |
| 21) Two fan carts labeled A and B are placed on opposite sides of a
table with their fans pointed in the same direction as shown in the figure
below. Cart A is weighted with iron bars so it is twice as heavy as cart
B. When the fans are turned on, they provide a constant force of the cart
independent of its mass. Assume that friction is small enough to be neglected.
The fans are set with a timer so that after they are switched on, they
stay on for a fixed length of time, Dt, and
then go off. |
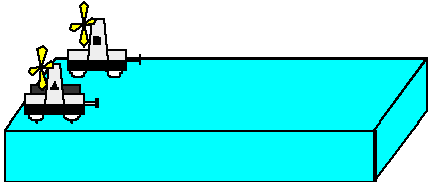 |
| (a) Just after the fans go off, which of the following statements
are true about the momenta of the two carts?
(b) Just after the fans go off, which of the following statements
are true about the kinetic energies of the two carts?
(c) Which of the following statements are true? You may choose as many
as you like, or none. If you choose none, write N.
(i) After the fan is turned on, each cart moves at a constant velocity,
but the two velocities are different from each other.
(ii) The kinetic energy of each cart is conserved.
(iii) The momentum of each cart is conserved.
|
22) Kinetic energy and momentum are both quantities that tell something
about an object's motion. Define what each one is and discuss the similarities
and differences between them.
23) Two blocks collide on a frictionless surface. After the collision
the two blocks stick together. Block A has a mass M and is initially
moving at speed V. Block B has a mass 2M and is initially
at rest. System C is composed of both blocks.

a) Draw a free body diagram for each block at an instant during
the collision.
b) Rank the magnitudes of the horizontal forces in your diagram. Explain
your reasoning.
c) Calculate the change in momentum of block A, block B, and system C.
Show all work.
d) Is kinetic energy conserved in this collision? Explain your reasoning.












![]()