Forces and Motion
or
What keeps the moon up there?


The Moon is a body with a radius a bit over $1000$ miles, and is a distance of around $240,000$ miles from the center of the Earth, which has a radius of just around $4000$ miles. So the Moon radius is just over $1/4$ (it's actally $27.3\%$) of the Earth and orbits a distance that is $30$ times the Earth diameter. If we were to draw things to scale, it would look like this:

The force of gravity, as originally figured out by Isaac Newton, says that the gravitational attraction of two bodies is proportional to the product of the masses of the two bodies, labeled $m_1$ and $m_2$, and inversely proportional to the distance $r$ between the center. That means you can write the formula for the force between the two bodies like this: $$F = G\frac{m_1m_2}{r^2}\label{newtongrav}$$ where for the Earth-Moon system, $m_1$ is the Earth mass, which is $6.0\times 10^{24}$kg (or $6.6\times 10^{21}$ tons), and $m_2$ is the mass of the Moon, which is $7.34\times 10^{22}$kg. Note that the Moon has a mass which is then only around $1.2\%$ of the Earth. The density ($\rho$) is defined as the mass per volume, and the volume of a sphere goes like the cube of the radius (V = $\frac{4}{3}\pi r^3$), so the average density is given by $$\rho = M/\frac{4}{3}\pi r^3\nonumber$$ If you calculate the ratio of the densities, the term $\frac{4}{3}\pi$ will drop out, leaving on the terms in $M/r^3$, so the ratio of the Moon to Earth denstities will be given by the ratio of the masses divided by the cube of the ratio of the radii, which is: $$\frac{\rho_M}{\rho_E} = \frac{m_M/r^3_M}{m_E/r^3_E} = \frac{(m_M/m_E)}{(r_M/r_E)^3} = \frac{1.2}{27.3^3} = 60.8\%\nonumber$$ That the moon is less dense than the Earth is interesting, and probably consistent with the fact that the moon has a much smaller magnetic field than does the Earth, which is telling you about the amount of iron in the Earth relative to that of the Moon (given that iron is associated with magnetic fields). But that's another story.
The question we want to address here is simple. What keeps the Moon up there, if it's only 30 diameters away from the Earth and definitely feels a gravitational pull. Shouldn't it have fallen into the Earth long ago? Answering this question brings out some amazing history of the development of modern science, starting with Plato and continuing up through Galilelo and Newton.
As a brief aside, the subject on the actual shape of the Earth, which is not a perfect sphere, is also interesting. If you want to learn more about this, click .
To understand why the Earth stays up there, we have to start with an understanding of forces and motion. And that understanding coincides with the birth of modern science, and that story starts with Copernicus (1473-1543, a 70 year lifespan) and ends with Isaac Newton (1643-1727, 84 year lifespan), and involves Tycho Brahe (1546-1601), Galileo (1564-1642), Kepler (1571-1630) and Descartes (1596-1650). The following timeline shows the relationship between these 6 giants, which spans 250 years and maps pretty well to the Renaissance period in Europe, which is probably not a surprise. It starts around the mid 15th century, around the time of Martin Luther (1483-1546). The century before we have the debacle of the bubonic plague (mid 1300s) that killed around a third of all Europeans, and over half of the population in the larger cities, and the Hundred Years' War between England and France that ended with the rise of Joan of Arc around 1428. So the context of this revolution in science is the context of a total change in society in Europe, a transition from the "middle ages" into something that leads to the modern era.

Nicolaus Copernicus was a scholar who lived most of his life in modern day northern Poland. His biggest claim to fame by far was in his considerations of the model for the universe, which goes back to the time of the ancient Babylonians, up through the Greeks and Romans. That model was deeply intertwined with religion, and the believe that what goes on in the heavens is the work of the God(s), and so had to be "perfect". And these ancients knew enough about mathematics to know that a circle was a "perfect" shape - all points are exactly the same distance from the center. And so, the universe had the Earth at the center, with the Sun and all the planets in orbit, in perfect circles. Easy observations of the Sun fit pretty well - the Sun rises in the morning and sets in the evening, and appears to follow a circular path around the Earth. But on closer look, that doesn't account for details, like variations in the Sun's "orbit" for different seasons. And observations of the planets were way more complicated than could be explained with perfect circles. The planets were a big problem for the ancient cosmology, and Mars, being easy to spot in the night sky, was clearly not following a circle.
To understand this, note that Mars is a red planet due to the predominance of iron oxide (rust). It looks like a red star, but it's easy to differentiate a planet from a star: stars blink, planets don't. To learn more about exactly why this is, click .
So Mars is red, it doesn't blink, and it's relatively close to the Earth, so it's bright and easy to spot. Which means it's easy to measure, and those measurements by the ancient astronomers showed that Mars (and the other planets) did not behave like stars in their orbits. (In fact, the word "planet" comes from the Greek term asters planetai, which means "wandering stars".) To understand why planets "wander", look at the simulation below, and hit the Start button.
Trace Mars
On the left is a solar system where the sun sits still, and the Earth (blue) and Mars (red) travel around in circular orbits, with different distances and orbital periods. (Yes, the orbits are elliptical, not circular, but the ellipse is close to being a circle, and for now it won't matter.) In the simulation on the right, however, we watch the movement of the sun and Mars relative to the Earth: the Earth-centered system, as envisioned by the ancients. The path of Mars is drawn with dashed lines, but you can uncheck the checkbox to get rid of that if you want.
You can see that from the point of view of someone on the Earth, Mars has anything but a circular orbit. Note however that this is not easy to see with the naked eye, it took some precise measurements using things like quadrants, sextants, etc. But when the competent ancient astronomer made the measurements, it's pretty clear that Mars was not going in a circle. Also, as you can see, the distance between the Earth and Mars changes quite a bit over time, and this is why when NASA contemplates missions to Mars, they have to take care when to launch.
The yellow line pointing away from Mars in the Earth centered simulation indicates the direction and speed of Mars, as observed by someone standing on the Earth, just to give you an idea of how Mars might have seemed to an observer. Note that this yellow velocity vector points mostly in the counter-clockwise direction, but at some point goes to zero and changes direction, even if briefly, and points in the clockwise direction. This apparent change in the velocity direction of Mars is referred to as "retrograde" motion, and it is the challenge of explaining this motion using the perfection of circles with the Earth at the center that challenged the ancients.
The following is the result of observations made by Tycho Brahe that were drawn up by Johannes Kepler, after a lot of calculations, in order to try to figure out what was going on. It must have taken Kepler quite a long time to take all of the observations made, and turn it into the picture below. You can see the retrograde motion where the planets makes it's closest approach to Earth, turns around for a short time, turns around again, and picks up speed as it heads out.
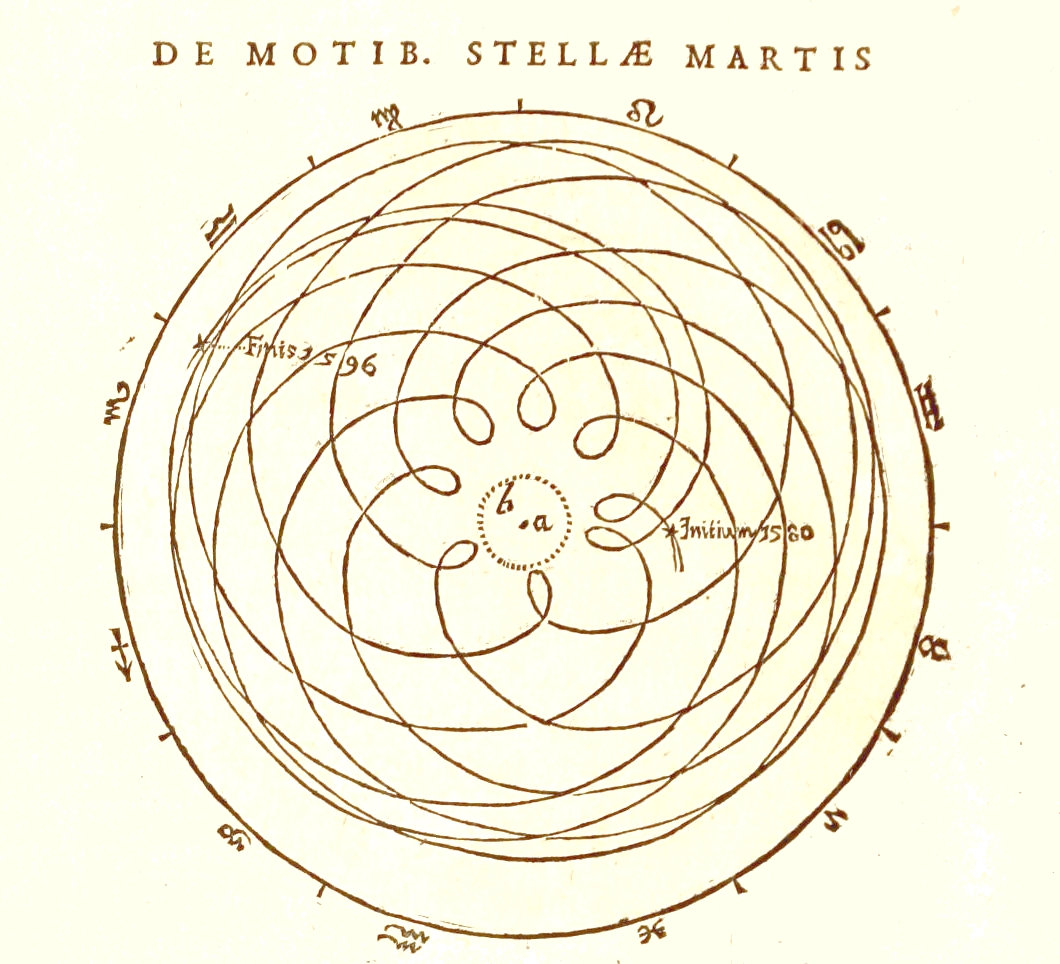
Figure 1. Mars as seen from the Earth as plotted by Kepler.
This diagram must have puzzled the ancient astronomers, who were fixated on ideas having to do with God, and the inherent perfections of whatever that God (or Gods) were to bring into being. Surely planets and suns have to orbit the Earth, which they were sure was at the center of the universe, and surely the orbit has to be in perfect circles, reflecting the perfection of the heavens. Yet the data said otherwise. This illustrates the age old problem of what happens when faith collides with observation!
The ancient cosmologists had quite a problem to solve, and so they searched for a model that
would not only be consistent with their faith - an Earth-centered universe and all motion
in perfect circles - and be consistent with the irrefutable observations of wandering stars.
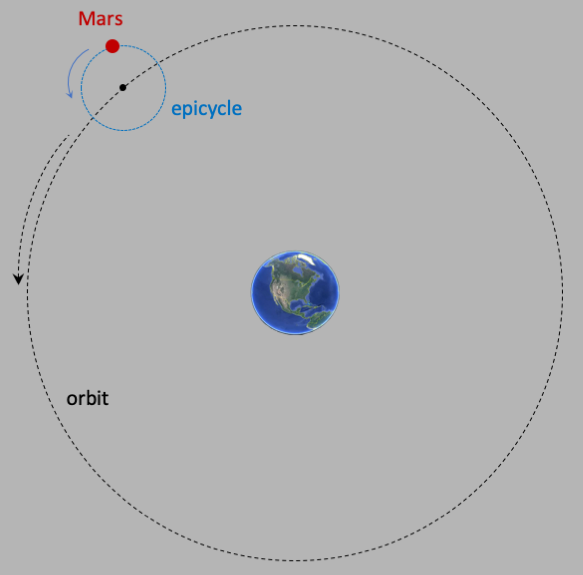
The idea is actually quite brilliant! They theorized that the planets
(and the Moon and the Sun) move in a circular orbit around the center of a circle
(that circle is called an epicycle), and the center of that circle orbits around
the earth in a perfect circle, as in the following figure:
You can see how this works in the simulation below. The yellow circle is the epicycle, and
Mars orbits about the center (the small open red circle). The large white circle is
called the deferent, and that is the circle about which the epicycle center orbits
around the Earth, which is still at the center of the universe.
You can adjust the ratio of the
epicycle radius ($R_e$) to the deferent radius ($R_M$), and you can adjust the
ratio of the epicycle period (the time for once around, $T_e$) to the deferent period ($T_M$),
just to see how the orbit depends on those parameters.
The initial values are set to 0.8 and 0.5 respectively. The path of Mars is drawn as
dashed lines, where
the length of the dash is proportional to the velocity (you can uncheck the "Trace Path" box
if you want to see the path without being drawn).
Trace Path
Epicycle to Mars radius ($R_e/R_M$)
= 4/5
Epicycle to Mars period ($T_e/T_M$)
= 1/2
If you run the simulation for a few orbits, you will a pattern that is similar to the picture
that Kepler draw (see Figure 1 above). But there are problems with the
epicycle theory. For instance, you can see that the size of the "lobes" (the oval shape of
the path of Mars when it is closest to the Earth) are all the same in the simulation, but they
are different in Kepler's diagram. You can also see that the lobes are distributed uniformly
around the Earth in the simulation, but again not in the diagram. These lobes describe what
is called "retrograde" motion - where Mars appears to move in the opposite direction (as seen
by an observer on Earth) than what is usual.
In fact, it was the attempt to understand and reproduce retrograde orbits that
caused people to try using epicycles.
As described above,
the prevailing theory before Ptolemy described the universe as being Earth-centered, with the
Sun, Moon, planets, and stars all moving in circular orbits (deferents)
about the Earth, making use of
epicycles as needed.
In this theory, the center of the deferent coincided with the center of the Earth,
and the motion of the center of the epicycle was uniform around this same center so that all
3 coincided (center of motion, center of Earth, center of uniformity).
This theory was in use by the 3rd century BC (if not before),
and endured for five hundreds years
in it's form, while the astronomers (or philosophers) made increasingly accurate observations.
And those observations showed that faith and data were inconsistent, and in need of something
more in order to be reconciled.
This is where Claudius Ptolemy of Alexandria, Egypt, started in the 2nd century AD
when he wrote and published his famous book about the orbits called "Almagest".
This book not only synthesized the then-current theory of cosmology, but added some changes
to bring faith and observation into agreement.
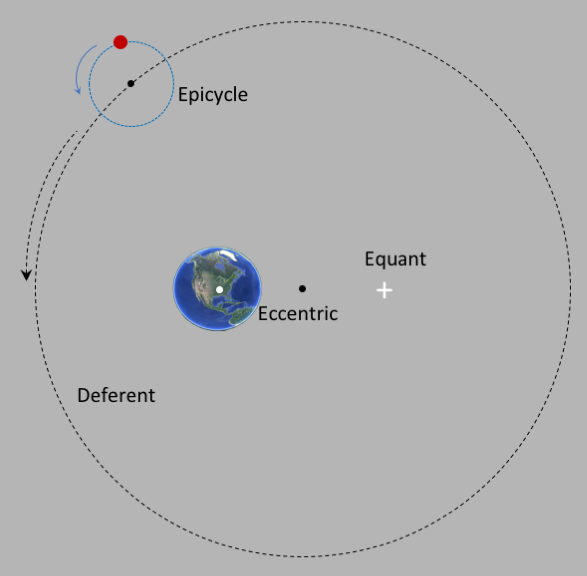
In this book, Ptolemy's theory preserved both the deferent and epicycle,
but he separated the 3 centers (Earth, deferent,
uniformity) as necessary to get the most accurate
predictions.
The following figure shows Ptolemy's system for the planet Mars moving around the Earth.
Mars moves at a constant angular velocity (angles per second) in a circle, around the epicycle,
shown in blue.
The center of the epicycle moves
in a circular orbit called a "deferent" at a constant radius from
the center, called the "eccentric". The center of the Earth is off axis, some distance
from the eccentric. The real genius of Ptolemy was in postulating that the orbit of
the eccentric was not uniform around the deferent circle, but was instead uniform about
a point called the "equant", which was on the other side of the eccentric from the Earth
along the same line.
This means that the angular velocity of the epicycle center is constant relative to the
equant, but the orbit path of the epicycle center is circular around the eccentric.
Complicated, but summarized in the following:
The simulation below implements the Ptolemaic system, with some reasonable guesses for
the parameters. The eccentric is shown as a small black dot, and the equant as a small
white cross.
You can change the radius of the epicycle (in AU, or "astronomical
units", which is the distance from Earth to the Sun), and you can change the period of the
epicycle around the deferent center. The presets are pretty good for reproducing
Mars' true motion as seen by an observer on Earth.
Hit the Start button let it go for several revolutions. You can see that the
pattern looks pretty similar to the picture in Figure 1 above.
In fact, Ptolemy's approximation is so good that modern day planetariums use Ptolemy to project
the position of the planets onto the ceiling!
Trace Path
Mars epicycle radius (in AU)
Mars deferent period (in years)
The first known proponent of a sun-centered (heliocentric) cosmology was made by
the Greek philosophyer Aristarchus, who lived on the island of Samos (just off the west coast
of Turkey) around 270 BC. Most of what is known about Aristarchus comes from Archimedes,
and it is probably the case that other people of that era had come to similar conclusions.
Islamic scholars in the medeival period wrote extensively of a sun-based system, and made
observations used in their theories, and these theories were surely well known by scholars
in Europe by the time Copernicus (1473-1543)
came on the scene, around 1500, when the geocentric model of the universe was probably hanging by
a thread. This was an incredible
period for Europe: the discovery of the new world; the rise of the corrupt Medici popes;
the incredible artistic creativity of people like Michelangelo,
Leonardo da Vinci and Hieronymous Bosch; and the beginning of the end of the
dominance of the Roman Catholic church what with the establishment of the Church of
England under Henry VIII and the beginnings of the Protestant movement under Martin
Luther. Just to name a few!
Since the Ptolemaic systems seemed to be "reasonably" predictive, what was Copernicus
after? This is hard to say for sure, but one component was probably the
increasing amount of data from
observations, and the weakening of the Roman church over all intellectual thought,
and that means scholars like Copernicus were less reluctant to indulge in inquiry.
And Copernicus probably still believed in the Ptolemaic principles of divine
perfection. But his theory of a Sun-centered cosmology was simpler, and arguably
more "elegant" than that of Ptolemy, and so he pulled the string and wrote the
seminal "De revolutionibus orbiam coelestium", published at the urging of
his student Rheticus the year of his death in 1453.
The Copernican system was simpler: put the Sun at the center of the universe,
and have the planets orbit around the sun using deferents and epicycles, and add
epicycles on epicycles as needed to reproduce the data. And have the stars orbit
around the sun at a radius so far away as to be almost infinite with respect to the
radius of the Earth's deferent. Copernicus also added in the effect of the
apparent measurement of the planets' orbits due to the rotation of the Earth
about its axis, once every day.
The following is a reproduction of the cosmology diagram that appeared in
De revolutionibus orbium:
Tycho Brahe (1546-1601) was born just a few years after Copernicus published
De revolutionibus. Brahe was extraordinary - an astronomer who made his own
instruments and over a period of many years accumulated a fantastically accurate
set of measurements of the positions of the planets, without the aid of optical
instruments like telescopes, which did not come on the scene until around 1600.
He was a Danish nobelman, educated in Germany, studying medicine among other
things. At the end of 1566, he got into a drunken sword fight with one of his
distant cousins, arguing over who was a better mathematician (those were the
days!), losing the bridge of his nose. He wore a prosthetic brass nose for the
rest of his life.
In around 1575 he was given an estate on the island of Hven,
a small island, maybe 3 square miles, in the sound between
Denmark and Sweden, just south of the castle in Shakespeare's play Hamlet.
You can imagine the long cold winter nights, with very little humidity,
and not much else to do but gaze through hand made instruments at stars and planets,
and record the data. It's a
wonderful visit if you are ever near Copenhagen.
Brahe had his own theory of cosmology, backed up by his observations, and not
very widely accepted. However
his observations stood alone as being the most comprehensive and accurate.
He built his own instruments, and
his setup at Hven included a paper mill and one of the first printing presses (so
that he could publish his own work!). He was a difficult person, dictatorial
over the people on Hven, however he was not politically ambitious.
And, as was common in that time period, astronomy and
astrology were basically thought to be the same thing, and Tycho also served as
the royal astronomer, presenting a yearly Almanac with military and political
predicts. Perhaps this was the way astronomers got support, by delivering
astrological predictions.
In 1588, his royal patron died, leaving the Danish
kingdom in control of people who did not sympathize with his talents.
He struggled on at Hven, but in 1597 left for Prague to become the imperial court
astronomer to Emperor Rudolff II.
He then set up
an observatory, made further measurements, and was assisted by students,
among them the brilliant Johannes Kepler.
Brahe had his own cosmology, sort of a compromise between Ptolemy and Copernicus,
that had the Sun and Moon orbiting the Earth, with all the other planets
orbiting around the sun, in perfect circles, with epicycles, and rejected the
idea of a rotating and revolving Earth as being in conflict with religious dogma.
He died in 1601, apparently of complications from uremia (rumors of Kepler poisoning
him were debunked after exhuming his body and doing tests in 2010).
He wrote his own epitaph: "He lived like a sage and
died like a fool".
Johannes Kepler, (1571-1630) was born some 30 years after Copernicus published
De revolutionibus. The debate between geo- and helio-centric cosmology was still
raging, and in fact was not really settled until the early 1700s when measurements
of the positions of stars between 6 month observations were shown to differ. This
could only be true if the Earth were not the fixed center of the universe
with the stars in orbit an infinite distance away, and so was probably the last
straw in the geo-centric cosmology.
Kepler began working with Tycho Brahe in Prague a year or two before Brahe died.
Brahe was notoriously fussy about who could use his data, and wouldn't let anyone
copy it and take it away for their own use.
Apparently Brahe was impressed with Kepler enough to let him look at it, but not to
copy it, so progress was slow. When Brahe died in 1601, Kepler was appointed his
successor, and was therefore free to make use of
all that precision data, to make progress in his studying the orbit of Mars, and
to understand Figure 1. Note that by this time, the data
were getting better (more accurate), and there was more of it, and telescopes were
making precision cosmology possible.
By 1605, Kepler had figured out something revolutionary: if you assume Copernicus'
helio-centric system, and postulate that the
orbits of the planets were were not circles at all, but instead
were elliptical, you could reproduce the data to a higher precision.
In 1621 he publisehd Epitome astronomiae Copernicanae, a treatise on the
Copernican heliocentric cosmology, complete with elliptical orbits and relationships
between the orbital period of planets and their distance from the sun as summarized in
3 laws ("Kepler's Laws of Planetary Motion"):
The following
table shows the data using current information, which is of course much more precise than
what Kepler used.
You can see that the quantity $d^3/T^2$ is pretty close to 1 for all the planets, but of
course Kepler didn't know that when he started looking closely at his data.
So why would Kepler even try looking for patterns? Well, perhaps he made something like
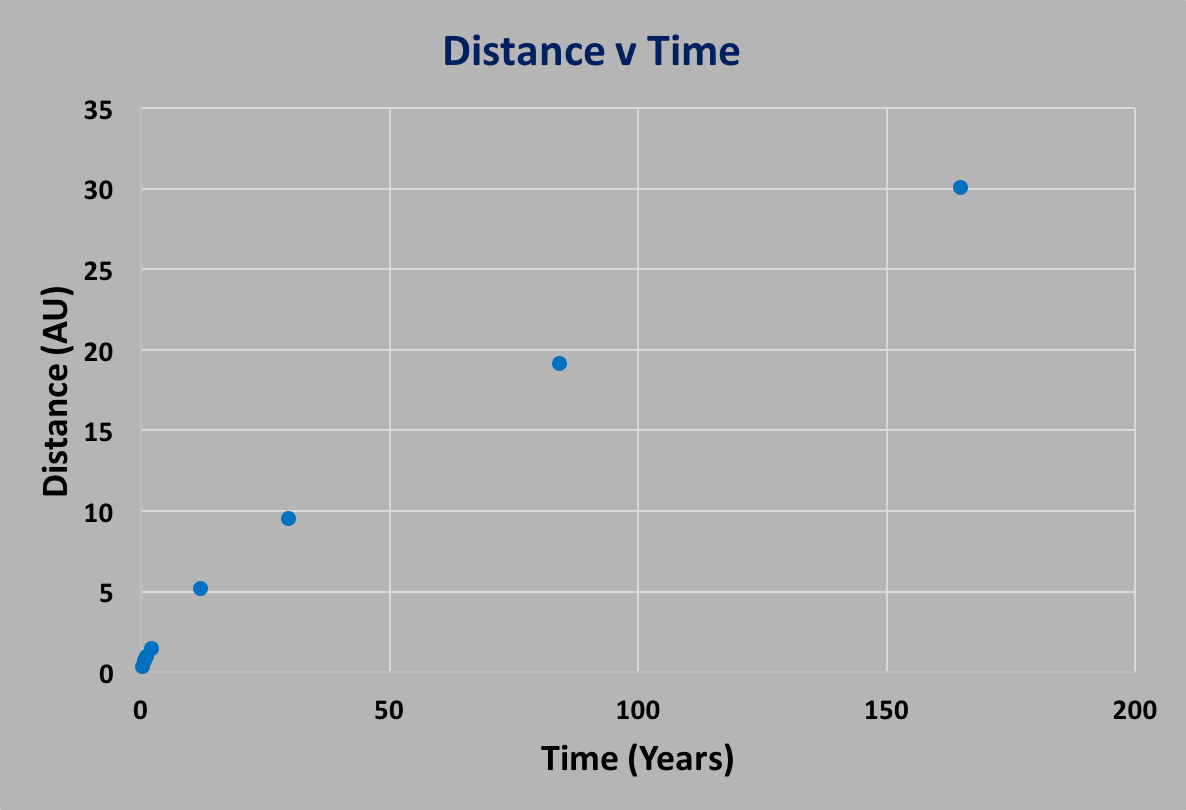
the following figure, plotting distance (in AU, where 1 AU = earth-sun distance) vs time
(in years). Each blue dot contains data from one of the 8 planets in the above table:
As you can see, there's certainly a relationship. Modern day analysis techniques would
fit the curve of $d(T)$ and find that $d=T^p$ where $p$ is some power, found to be $p=2/3$,
but Kepler showed that this was
true from observations, not from any first principle calculations.
But Kepler did not have modern computers and mathemtics, and so discovering this
must have been pretty amazing.
Especially in an era that was still dominated by mysticism.
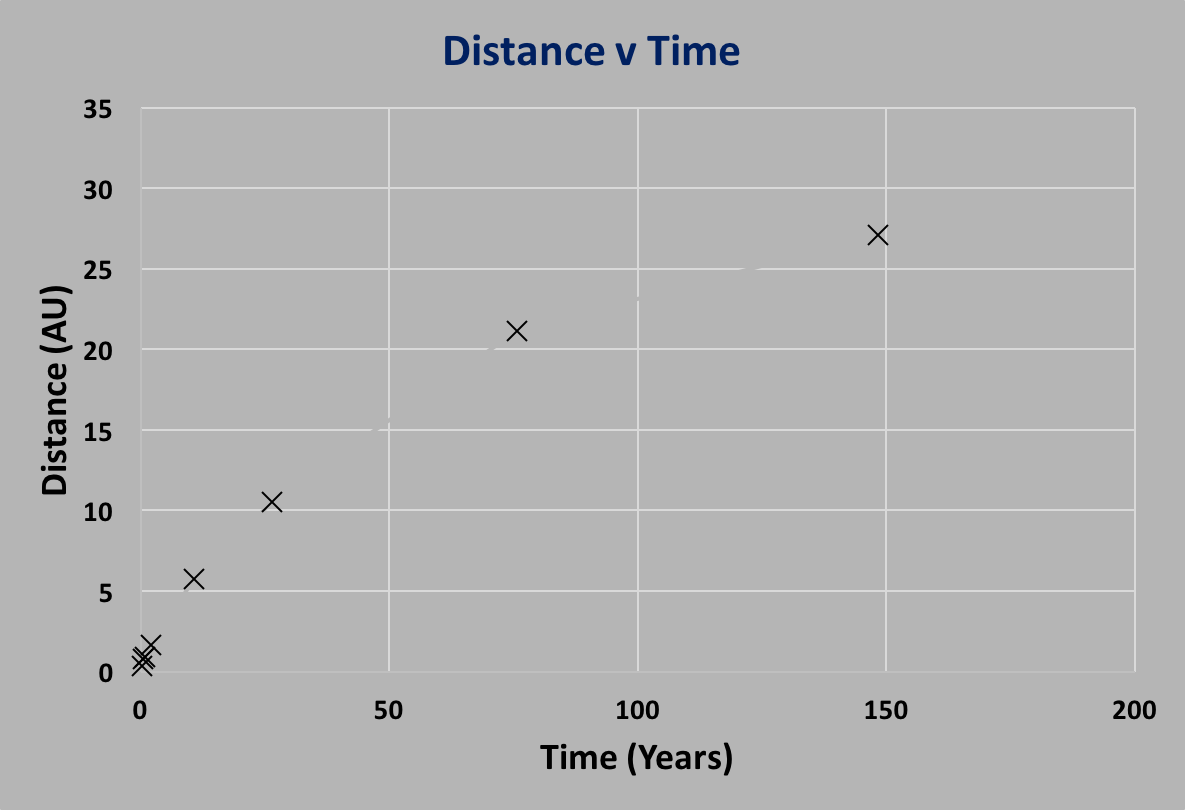
Of course, Tycho Brahe's measurements were not nearly as precise as what can be measured today
with modern telescopes and equipment. So you might ask whether the measurements Kepler used for his
good enough to bring out the 3rd Law relationship. In the following figure, the data shown
are fluctuated randomly at the $10\%$ level, shown
as black crosses. You
can see that the data do not line up as well as the "correct" data, but it's still easy to see
that there's a relationship.
Anyway Kepler's laws are fundamental, we teach them all the time. But when Kepler published
them, he still did not know why these laws worked.
Before we get to Newton, we have to first discuss Galileo Galilei (1564-1642) and
Rene Descartes (1596-1650). Galileo and Descartes were contemporaries, although Galileo was
a generation older. But these are the two main bridges that leads to Newton, and the
birth of the modern era in physics and science.
Galileo was a complex person, with a huge impace. He introduced
the telescope to serious astronomy, and seriously rethought the dogma of Aristotle and physics
(getting into hot water with the Catholic church and religious dogma, a fascinating
story).
For instance, Aristotle said (quite rationally) that a body in motion will tend to slow down,
because that's its nature, and that bodies would fall at a rate in proproportion to their weight,
so that the bigger the mass, the bigger the acceleration.
That surely makes sense as far as observations go.
But observations are not the same thing as actually doing a controlled experiment,
and Galileo was one of the first to do real experiments to see what
happens.
Arguably his most famous was in measure the free fall time for different masses to show that
it was not a function of the mass (providing friction can be neglected).
There is some disagreement as to whether he actually did these experiments
off the Leaning Tower of Pisa, or just used inclined planes, and most people believe it was
others who actually used the tower.
Regardless, conclusions from this experimental work
refuted the dogma of Aristotelian physics, and the whole
approach of thinking of things and classifying them by how they behave.
For Galileo, it was completely different, and the beginning of modernity - that there are
underlying principles that one can apply in order to understanding things like motion.
Galileo published seminal books about physics, and mechanics of motion, but in his time these
results were not like current textbooks, full of mathematical formulae that describe the laws
of physics. Galileo, the "father of modern science", mostly used words and tables.
Formulae had to wait for the French philosopher,
mathematician, and genius Rene Descartes.
Rene Decartes (1596-1650) was a philosopher of the first rank. The proof?
In 1637 he published "Discourse on the Method of Rightly Conducting One's Reason and
of Seeking Truth in the Sciences", a treatise that addressed the role of reasoning in
understanding science and nature, and the importance of skepticism as a starting point
for everything and how to be thorough in establishing any truth. He discussed ethics
(morals), and the role of humility ("...endeavor always to conquer myself rather than fortune...").
In Part IV of this book, he pretty much gives birth to modern philosophy,
discussing ideas about perfect knowledge, the nature and source of
doubt, the relationship to reason, and how we can even know anything at all.
This is where he first used the phrase "cogito ergo sum" (I think therefore I am) as a way
of refuting whether we should doubt everything because we can't know anything.
Today we all know and agree that
mathematics is the "language" of physics, and if you look in any physics text, you will
see the language in the form of mathematical formulae.
But up until the early 1600s, this was not the case: physics was not yet a "science" as
we know it, astronomy and astrology were thought to be the same, and doctorates were
of philosophy (PhD!).
The introduction of mathematics as the language of the physical sciences
not only describes natural phenomena precisely and unambiguously, but embodies the
whole idea of a one to one relationship between natural phenomena and mathematics that
ushered in a whole new world emphasizing objectivity over mysticism.
Contributing to this transition is arguably where Descartes had his biggest impact, in
the develoipment of "analytic geometry".
To understand analytic geometry, start with a circle:
Descartes saw the same circle, but he took it a step further: he
assigned values to those points, and in order to be able to do so, he needed references.
So he invented the "Cartesian" coordinate system, as shown in the figure below.
This coordinate system consists of 2 axes, one labeled
$x$ and one labeled $y$, and the points along the circle are identified by their
distances from those axes. Or to put it another way, if you were start at the "origin"
$x=0$, $y=0$ and walk to some point on the circle, the coordinate tells you the distance
you walk along $x$ and the distanc you walk along $y$.
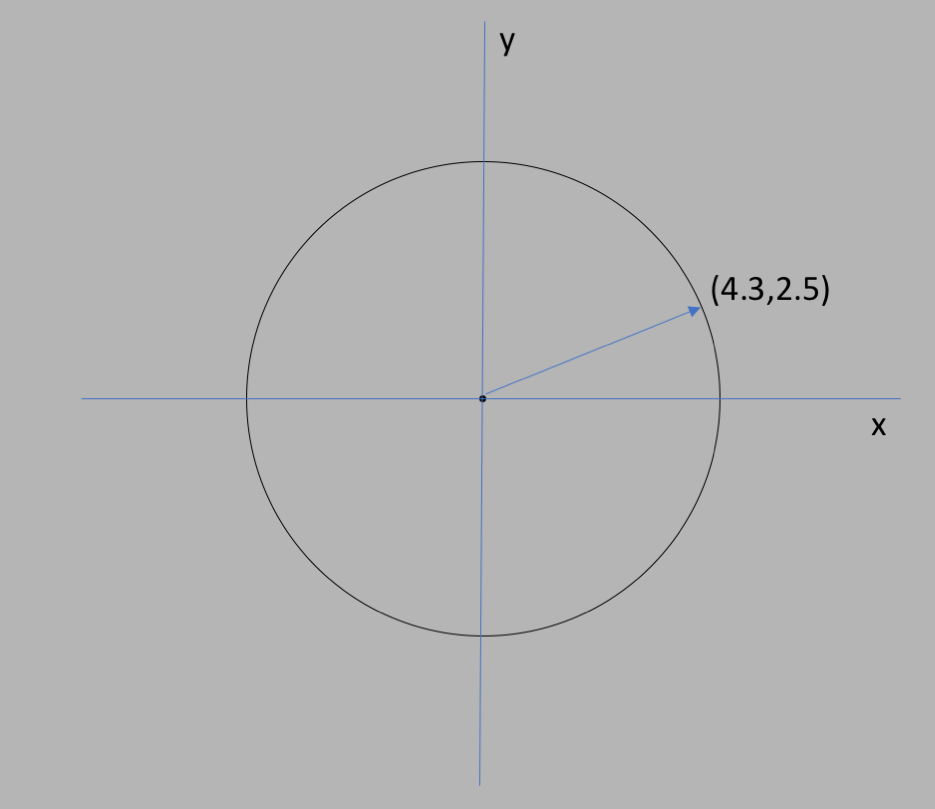
For example, in the figure below, you go out
$4.3$ units along $x$ and then $2.5$ along $y$, and that would be a point that was on
the circle. Note that it doesn't matter whether you first walk along $x$ and then
along $y$, or vice versa.
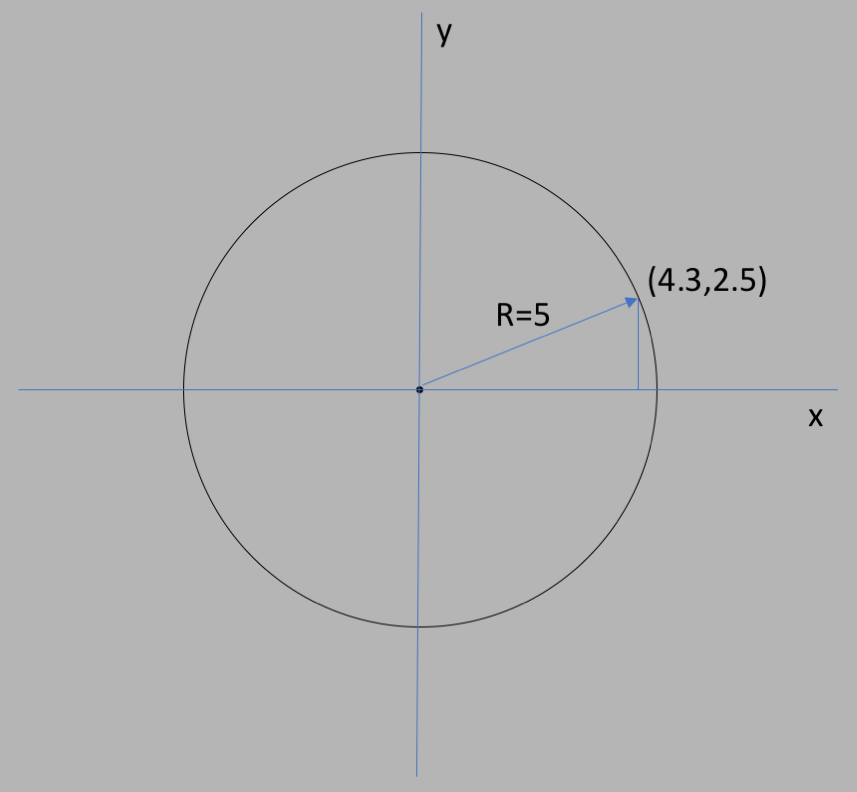
Let's say that the radius of the circle is $5$ units. Then the perpendicular to the
$x$ axis makes a right triangle with some length along $x$, and some length along $y$,
and a hypotenuse of $5$. From the Pythagoras theorem we know that:
$$x^2 + y^2 = 5^2 = 25\nonumber$$
And that for any value of $(x,y)$ on the circle, it will satisfy that formula.
This is what is known as "analytic geometry". And it's amazingly powerful, as it
can describe any figure, or any "curve" (aka path) in the $x-y$ plane, and
allows one to describe these curves via sets of points that are all related by
a formula.
For example, imagine you throw a ball up in the air, and the height of the ball is the $y$
variable (or you can call it $h$, it's just a variable name).
If you throw in any direction along the horizontal, then that direction is
described by the $x$ variable which measures horizontal distance.
Descartes' philosophy says that you should be able to
describe the relationship between $x$ and $y$ using some kind of analytic algebraic
formula, and his system of coordinates tells you how to do it. But it doesn't
tell you what that formula is, for that you need some kind of physical principle.
And this is exactly where Isaac Newton enters the picture,
synthesize everything that went before him, into a coherent usable description of the physical world.
The whole story of Newton is also fascinating. He was a mystic, dabbled in
alchemy, was very religious,
a loner and a total enigma.
He was fascinated by scripture, and the Book of Revelation, and looked for mathematical
meaning (aka numerology). And, he pretty much invented calculus and modern physics!
He never married, and after his funeral, Voltaire reportedly
said ("Letters on England", page 100):
"...was never sensible to any passion, was not subject to the common frailties of mankind,
nor had any commerce with women—a circumstance which was assured me by the physician and
surgeon who attended him in his last moments"
Newton threw Aristotlian philosophy on its ear, debunking it thoroughly, by introducing
a well defined set of laws, described by mathematics, allowing precise predictions.
And Newton's laws have passed the test of time, still in use. They are superceded by
Einstein's laws of relativity and by quantum mechanics in the modern era, but those
Newton and Einstein only differ when considering velocities approaching that of light,
or the behavior of fundamental particles and systems of atoms on microscopic and
sub-microscopic scales.
For all "classical" phenomena (classical means not relativity and not quantum mechanics),
Newton's laws are what we use.
Before continuing onto Newton's laws, it is probably best to abandon (somewhat) the
historical progression. The development of mathematics goes hand in hand with the development
of physics, however mathematics is a curious thing, where the development of the math and
the development of the notation do not sometimes coincide, and in fact the modern
notation is often developed way later than the mathematics.
Anyway notation is extremely important,
so we will skip ahead to where the notation is settled, and then use the modern notation
to show the progression of mathematics as it led from Descartes to Newton.
First let's consider motion of just a single
particle along a single direction, and how we describe the motion
(but not necessarily the dynamics of what makes things move).
As good Cartesians, we label the coordinate of the particle as $x$, and we want to
know where it is as a function of the time $t$. So we want to know the equation that
governs $x(t)$.
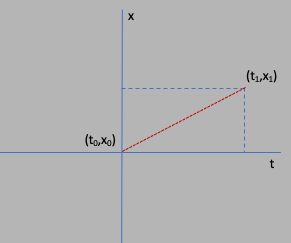
The situation is as presented in the following diagram: we go from an initial position
$x_0=0$ at a time $t_0=0$ (aka the "origin"), to a position $x_1$ at a time $t_1$.
This concept of "origin" is a key thing in math and physics - you will find that in the
more advanced subjects, the equations tell you how things change, so you have to add in
your own initial conditions, as we do here.
In the above animation, the position $x$ measures the displacement of the red ball from
the center of the yellow line where the green line crosses. This is the "origin", and
has the coordinate $x=0$. The time $t=0$ is when you start moving, and $x$ is positive
to the right and negative to the left.
Notice the correlation between the speed that you move the ball, and
the slope of the $x$ vs $t$ curve to the right, where $x$ is the vertical coordinate and
$t$ is the horizontal. As you can see, when you move the ball fast, you see a
steep slope, and when you move the ball slowly (if at all), the slope is horizontal.
This is a key concept in physics and calculus: the rate of change with respect to time
of some quanitity $x$ is reflected in the slope of the $x$ vs $t$ curve.
The goal of this animation is to give you
a feel for how to relate motion to the shape of the curve, especially the slope at any
point.
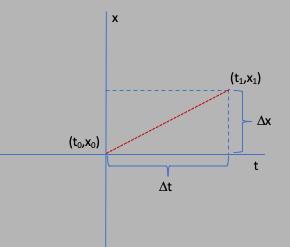
The slope is defined as the ratios of the change in the vertical quanitity, to the
change in the horizontal. So as in the figure below, when you move from position
$x_0$ at $t_0$ to a position $x_1$ at time $t_1$, you move through a distance
$\Delta x=x_1-x_0$ in a time $\Delta t = t_1 - t_0$. The slope of the straight line
that connects the two coordinates is given by the ratio $\Delta x/\Delta t$.
Something moving will have a velocity that measures "how fast", with units
of "miles per hour", or "meters per second".
The velocity tells you about the rate of
change of position with respect to time, which means how far ($\Delta x$) in what
time interval ($\Delta t$).
This is why we can define the velocity $v$ of something moving as:
$$v = \frac{\Delta x}{\Delta t}\nonumber$$
We can unravel the above equation to write
$$\Delta x = v\Delta t\nonumber$$
or
$$x_1 = x_0 + v\Delta t\nonumber$$
Now let's be a bit more general, and drop the subscript for $x_1$, and just let $x_1$
be the variable $x$. This means $x_0$ is the initial value of the position, and $\Delta t$
can just be the time $t$ as measured from $t=0$ at $x_0$. So we start the
clock when the particle is at $x_0$, and stop it at some time $t$ when the particle is
at position $x$. The above equation
tells us that starting at $x_0$, or as is often the case we say $x_i$ ($x$-initial),
if you know the velocity $v$, then you can calculate
the position $x$ from the formula
$$x(t) = x_i + vt\label{xvt}$$
This formula describes a straight line in the $x$ vs $t$ plane, with constant slope $v$
(constant velocity).
In the next figure,
the velocity is not constant, as is often the case in a world
that is not so simple!
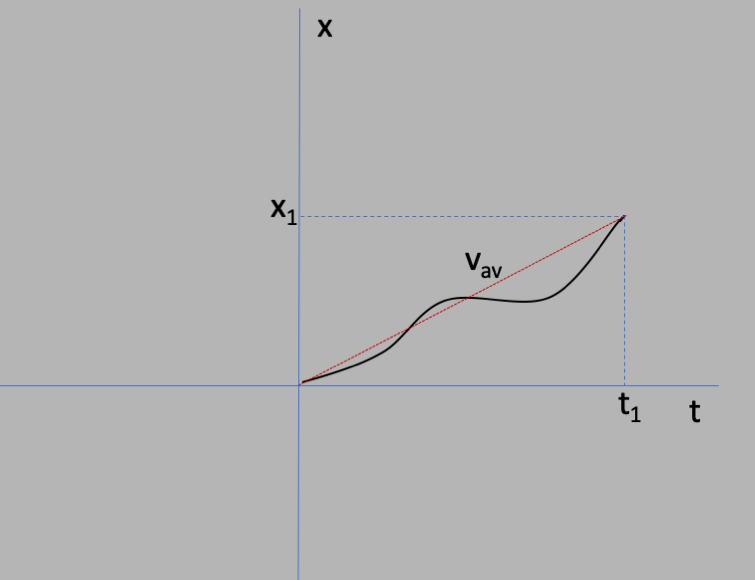
The path from the origin $t_0=0$ is along the curve, which does not have a constant
slope (that is, the velocity changes with time). But if we know the average
velocity $v_{av}$ between the initial point $(t_0,x_0)$ and the final point $(t_1,x_1)$,
then we could use equation $\ref{xvt}$ with $v=v_{av}$:
$$x_1 = x_0 + v_{av}t_1\nonumber$$
By definition of what it means to make an average value of some quantities
over the interval, the average of the velocity will be given by
$v_{av} = \half(v_0 + v_1)$, where $v_0$ is the velocity at the initial
point, and $v_1$ at the final point.
Next, we use the definition of the acceleration, analogous to the
velocity, and calculate the velocity $v_1$ at $t_1,x_1$
in terms of the velocity $v_0$ at the origin $t_0,x_0$:
$$v_1 = v_0 + at_1\nonumber$$
Substituting for $v_{av}$ and $v_1$ gives
$$\begin{align}x_1 = & x_0 + v_{av}t_1 \nonumber \\
= & x_0 + \half(v_0 + v_1)t_1 \nonumber \\
= & x_0 + \half(v_0 + (v_0 + at_1))t_1 \nonumber \\
= & x_0 + v_0t_1 + \half at_1^2 \label{fa}\end{align}$$
Now we use the same "trick" that $t_1$ can be any time $t$, which gives the formula
$$x(t) = x_0 + v_0t + \half at^2\label{xvta}$$
and
$$v(t) = v_0 + at\label{vvt}$$
These are the formulae for the position $x(t)$ and velocity $v(t)$
at any time $t$ given an initial position
$x_0$, an initial velocity $v_0$, and a constant acceleration $a$.
What this says
in words is that a body at rest ($v_0 = 0$) will remain at rest if there's
no change in velocity ($a=0$), which is kind of obvious from equation
$\ref{vvt}$. But it says more than that - it also says
that a body with some initial velocity $v_0$ will remain at the same velocity
unless there's an acceleration that changes the velocity. Which totally refutes
Aristotle. Voila, modern physics!
Now we are ready to visit Newton. What he did in his famous Philosophiae Naturalis
Principia Mathematica, or Principia for short, published in 1687, set the
stage for modern science. Just around the time Newton published this, Johann
Sebastian Bach was born (1685), and in 1689
John Locke published his theories on currency and property,
religious tolerance, separation of church and state, and political theory in his book
Two Treatises of Government. The British monarchy was reestablished
in 1660, and Louis XIV reigned in France at the pinnacle of the French monarchy.
This is the beginning of the so-called "Age of Enlightenment", generally seen as the
transition from the medieval to the modern era in Europe, and of course the origins
of the U.S. Declaration of Independence.
The Principia laid out the 3 laws known now as "Newton's 3 Laws", synthesizing
almost everything that was "in the air" since the time of Copernicus, as discussed above.
There is, however, one small idea that Newton took for granted that we should mention
here, concerning motion, and how to describe it using analytical geometry (aka math).
This could easily be added to Newton's 3 laws as his 0th law:
This is a pretty revolutionary thing actually, but it makes perfect sense if you
start at the beginning.
So imagine that you are moving only along one direction. Then you
can use the variable $x$ to be the E-W displacement, and apply equations
$\ref{xvta}$ and $\ref{vvt}$.
Now let's say that your motion is not E-W, but instead NE-SW at $45\deg$.
However, E-W is a special direction that we use because it maps onto the spin rotation
of the Earth. The coordinate $x$ measures the displacement along the direction of
motion, not the displacement along the direction parallel to the Earth's rotation.
So if you were to
And, it also says that if there's no acceleration, then there's nothing too interesting
going on. But that if there's acceleration, then anything can happen, and the motion
can get interesting.
This means that if you understand the underlying dynamics of a physical principle,
and you have motion in the $xy$ plane, then you apply those dynamics to the
motion along $x$, and along $y$, as being completely independent.
To illustrate, let's first consider Newton's Laws:
All rights reserved. No part of this publication may be reproduced, distributed, or transmitted in any
form or by any means, including photocopying, recording, or other electronic or mechanical methods,
without the prior written permission of the publisher, except in the case of brief quotations embodied in
critical reviews and certain other noncommercial uses permitted by copyright law.
Epicycles
Ptolemy
This is a pretty amazing theory, in that in order to verify it, Ptolemy had to have lots of
accurate observations covering Mars' motion over many years. Ptolemy must have been as patient
as he was brilliant!
Copernicus (Heliocentric)

Tycho Brahe

One of Tycho Brahe's hand made sextents (l) and quadrants (r)
Kepler
This 3rd law says that the quantity
$$\frac{d^3}{T^2}\nonumber$$
is a constant, the same for all planets. Kepler came up with this law using observations
mainly made by Tycho Brahe (1546-1601), and mainly without optical instruments.
What Kepler did was to take the data, and play with it, looking for patterns.
That he found these laws is amazing, a testament to his persistence, mathematical
abilities, and the quality of the data.
1 AU = Earth-sun distance = 92,955,902 miles
Planet Distance (AU) Period (Years)
$d^3/T^2$
Mercury 0.38 0.240 0.974
Venus 0.72 0.615 0.999
Earth 1.00 1.000 1.000
Mars 1.52 1.881 0.992
Saturn 5.20 11.862 1.000
Jupiter 9.58 29.457 1.012
Uranus 19.21 84.021 1.004
Neptune 164.800 0.24
1.005
Isaac Newton (after Descartes and Galileo)

Kinematic Beginnings
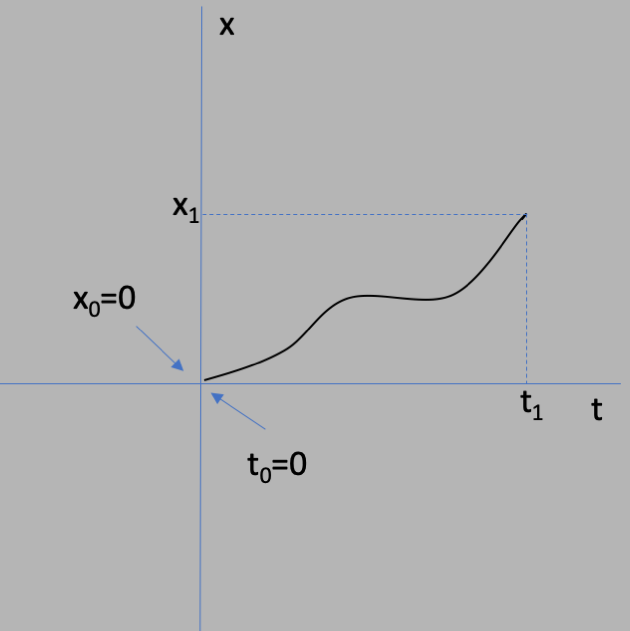
Newton's Laws
Copyright © 2019 by Drew Baden