Using Nonlinear Optics to Gain Insight into Superconductors, Liquid Helium, andBose-Einstein Condensates
Introduction
I’ve been looking into how we can use light to gain a better understanding of macroscopic quantum systems such as superconductors, superfluid helium, and Bose-Einstein condensates. Specifically, I’ve been looking into quantum vortices.
The focus of my first rotation was the relationship between quantum vortices in light, superconductors, superfluid helium, and BECs. I will save issues of entanglement for the second rotation.
Table of Contents
Quantum Vortices
How
to Create and Detect Vortices
A
Few Interesting Areas That May Need Further Study
Examples of Classical Vortices
The focus of my research is on vortices that occur in quantum systems. But first let’s get a feel for classical vortices by looking at a few examples
Figure 1 Three Examples of Classical Vortices (from left to right): a whirlpool in a glass of water, a tornado, and a smoke ring
A Solitary Wave
A vortex is a type of solitary wave. James Scott Russell was one of the early researchers into solitary waves. His report on solitary waves described the moment that inspired him to spend the next ten years of his life studying solitary waves:
I was observing the motion of a boat which was rapidly
drawn along a narrow channel by a pair of horses, when the boat suddenly
stopped – not so the mass of water in the channel which it had put in
motion; it accumulated round the prow of the vessel in a state of violent
agitation, then suddenly leaving it behind, rolled forward, with great
velocity, assuming the form of a large solitary elevation, a rounded, smooth
and well defined heap of water, which continued its course along the channel,
apparently without change of form or diminution of speed. I followed it on
horseback and overtook it still rolling on at a rate of some eight or nine
miles an hour, preserving its original figure some thirty feet long and a foot
to a foot and a half in height. Its height gradually diminished and after a
chase of one or two miles I lost it in the winding of the channel. Such in the
month of August 1834 was my first chance interview with that singular and beautiful
phenomenon . . .
Figure 2 A solitary wave created in the Union Canal
near Edinburgh done in homage to John Scott Russell
We’ve seen a solitary wave form in water. Do we have solitary waves and vortices in quantum mechanical matter waves? Let’s start by looking at the simplest case: a single non-relativistic particle.
A
free particle
When using non-relativistic quantum mechanics, two important states we often use are plane waves and Gaussian wave packets. Both these states can be used to gain insight into a wide range of quantum phenomena. When we move on to superconductors, superfluids, and nonlinear optics, solitary waves perform the role that plane waves and Gaussian wave packets had in one-particle quantum mechanics.
Plane waves are important because they are stationary states of definite momentum. Gaussian wave packets are valuable when representing a particle that is localized.
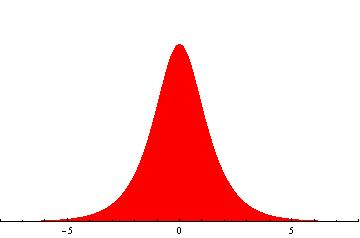
If a particle truly is in a state that is represented by a plane wave in position space, then the particle could be anywhere. On the other hand, for a particle is in a Gaussian state (see picture) it’s probably in between x=-3 and x=3. And what about the probability of the particle being far away? That probability goes to zero fairly quickly as you move away from the peak. In other words the particle is localized. So like the classical solitary waves, the Gaussian wave packet is localized. But unlike the solitary waves, the Gaussian wave packet doesn’t keep its shape over time. It keeps its same general from (it’s still a Gaussian) but the shape changes because the uncertainty in position increases with time. This is due to the uncertainty principle, or to use the language of waves, this is due to dispersion.
Dispersion
The phase velocity of any plane wave depends on the
momentum. Therefore, with time, a wave packet slowly disperses. For our
Gaussian wave packet: if we label the point where 
is a minimum
then, in position space, the state of the system at t=0 is given by
This is a plane wave, 
, modulated by a Gaussian, 
. It is also called an envelope wave. I imagine that it gets
the name, envelope wave, because it’s kind of like a plane wave, , packaged inside of an envelope specified by, .
Schrodinger equation
The dispersion of free, localized matter waves is captured by the Schrodinger equation,
This equation captures the dispersion relation we were discussing earlier,
This means that each plane wave has a different phase velocity which is what causes the dispersion.
Bose Einstein Condensates
Now instead of a single free particle, let’s look at the case where we have many particles for example when we’re talking about BECs. If we look at one particle in a many particle system: it feels the influence of all the other particles therefore it is no longer free.
In the case of BECs near absolute zero, in many situations their behavior can be described by a single coherent ‘wavefunction’. Using the mean field approximation, the equation describing this motion is the nonlinear Schrodinger equation,
The interaction between the particles leads to the nonlinear term. This potential is proportional to the number of particles in the vicinity.
Nonlinear Schrodinger Equation
The nonlinear Schrodinger equation describes envelope waves in a dispersive and nonlinear medium. Solitons and vortices can form because the nonlinearity counterbalances the dispersion. For example, in one dimension a solution of the nonlinear schrodinger equation is
This is localized. It also does not change its shape with time. It is a soliton.
In two (or more) dimensions, we can have vortices.
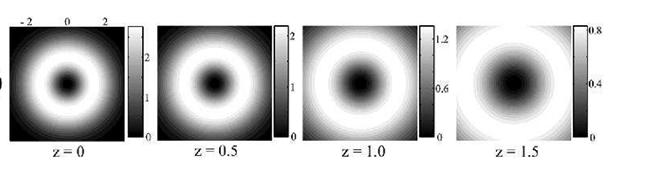
Figure 3
I light beam traveling in a linear medium. Like the single particle matter
wave, the light beam also experiences dispersion
As we said earlier, the nonlinear Schrodinger equation describes a wave packet that shows both dispersion and nonlinearity. And as we also said: when dispersion and nonlinearity counterbalance each other, vortices may form. Light traveling in a dielectric material shows dispersion because different frequencies have different phase velocities. We can describe the macroscopic effects of the dielectric by detailing how the polarization of the material depends on the electric field. For example, for a linear material we might write the polarization like so,
A linear dielectric shows dispersion but not nonlinearity. So in a linear dielectric, a localized wave packet will spread out as time goes by. In other words, the uncertainty in the position will increase with time just as it did for the free electron. And in many ways, coherent light propagating in a linear medium is analogous to the dynamics of a single particle.
But to find the analogy that we’re looking for, we need to shoot light into a nonlinear material. What I mean by a ‘nonlinear’ material is that when we look at the polarization of this material as a function of the electric field, it is now a nonlinear function.
So our hope is that if we shoot a laser beam into a nonlinear
material we will find that it behaves kind of like superconductors, superfluid
helium, and BECs. So what kind of nonlinear material should we choose. Since
we’re mainly interested in the counterbalance between the dispersion and
the nonlinearity, we don’t want to get sidetracked by nonessential
complications. So let’s choose a simple nonlinear material. Let’s
shoot a monochromatic light beam into a nonmagnetic, homogenous, isotropic,
material. If we expand 
as a power series
in terms of 
, then to lowest order the polarization would be given by[1],
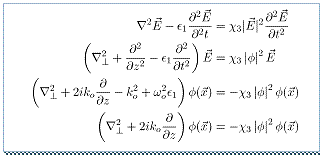The dynamics of the
light beam in this nonlinear material
So what happens when we shoot our monochromatic light beam into this material? All we have to do is look at Maxwell’s equations to get a pretty good idea. As we can see from the box, Maxwell’s equations imply that the electric field of our light beam is governed by the following equation,
Now in our case, we’re shooting a beam
that is a plane wave with frequency, 
, modulated by some function 
,
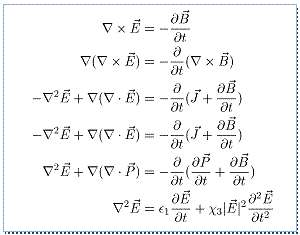
The simplest case is when the polarization
remains constant. In which case, the state of our light beam is described by , which is governed by the following equation,
Here, 
is the
laplacian in the (x,y) plane. So this is the 2+1 dimensional nonlinear
Schrodinger equation.
Dark Solitary Wave
We can have both bright and
dark solitary waves. If we have an attractive potential, then we can have a
bright solitary wave. In the case of a repulsive potential, we can have a dark
solitary wave. Here is an example of a dark solitary wave. It’s called a
dark solitary wave because the localized spot is dark instead of bright. Specifically,
this is a vortex.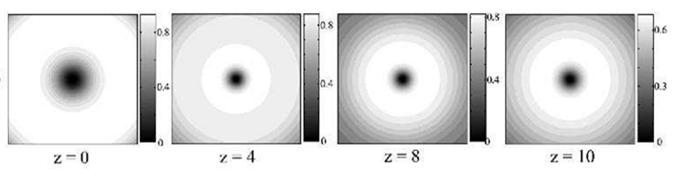 
Figure 4 A Dark Soliton
Liquid Helium
Rotating the Container
Suppose we pour some liquid helium into a cylindrical container. And the temperature is above the lamda point so right now it’s just a normal fluid (not yet cold enough to be a superfluid). Next, we start rotating the container, and the liquid helium starts to rotate with it. We continue rotating the container at the same speed and soon the liquid comes into equilibrium with it.
Now we cool the liquid down below 2.17K. Soon as we hit 2.17K, part of the liquid begins exhibiting superfluid behavior, while part of it continues acting like a normal fluid. The colder we make it, the greater the proportion of superfluid. So let’s take the temperature down to near absolute zero so that pretty much all of it is superfluid.
Once we’ve reached our desired temperature, we stop the container. What happens? If it were a normal fluid, then once the container stopped rotating, the liquid would also soon come to rest due to viscosity. But the superfluid? It will continue circling around a long, long time.
Quantized Angular Momentum
Now suppose we perform the experiment again. We do everything exactly the same as we did it last time with only one difference: we rotate the container more slowly. This time when we cool the liquid down, the liquid will stop swirling. it will stop swirling regardless of whether we stop the container or whether we let the container continue rotating. This is in stark contrast to a normal fluid which is pulled along by the container and is forced to rotate along with it. But the superfluid doesn’t necessarily rotate along with its container; instead its angular momentum is quantized. A superfluid system will enter into the state whose quantized angular velocity is closest to the angular velocity with which we were rotating our container. And if we don’t rotate fast enough to put it into the first excited state, the liquid will just sit there even though the container is spinning around.
Vortices
Each vortex call be thought of as a quantum of angular momentum and contains, at its center, a phase singularity around which the phase changes by a multiple of 2 pi. This 2 pi winding of the phase occurs for the same reason that deBroglie matter waves explain the quantization of angular momentum. The idea is simply that the matter wave is single valued, so that if you pick any point in space and label the phase at that point 0, then if you go around in a circle so that you come back to where you started then the phase must have changed by a multiple of 2 pi or not at all.
And the center of the vortex is a phase singularity. This means that the matter waves must vanish at the center. Although the normal uncondensed component of the system is free to inhabit the core. But there is no superfluid at the core of a vortex. Instead, superfluid flows with quantized circulation around each core.
Type II Superconductors
Applying a Magnetic Field
Quantization of magnetic flux
In a liquid helium superfluid, the angular momentum is quantized. For a superconductor, the magnetic flux is quantized.
Vortices
There’s a nice picture from the book, Basic Superfluids.
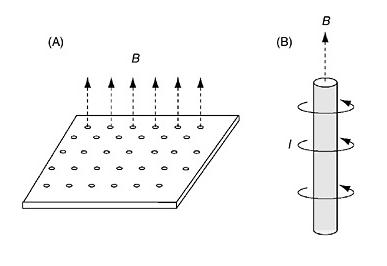
We have a thin sheet of type II superconductor. And we apply a magnetic field perpendicular to the sheet, the magnetic flux coming out of the superconductor is quantize. And like before, this creates a current in the superconducting material. And also like before, the magnetic flux is quantized.
We can detect the magnetic field by sprinkling a magnetic powder.
BECs
We can mimic the situation with liquid helium. We introduce asymmetries into our trapping potential to mimic the roughness of the liquid helium container. Then we can rotate the trapping potential which is analogous to the rotation of the liquid helium container. And vortices form in the Bose Einstein condensate similar to how vortices formed in liquid helium
Figure 6 Vortices in a BEC. The dark spots are the cores
of the vortices
.
We can also use a light beam that contains vortices and transfer the angular momentum to the Bose Einstein condensate.
Light
Choosing Initial Phase Pattern
If we take a coherent light beam, we can create the phase profile that we desire. So creating vortices simply amounts to creating the correct phase profiles.
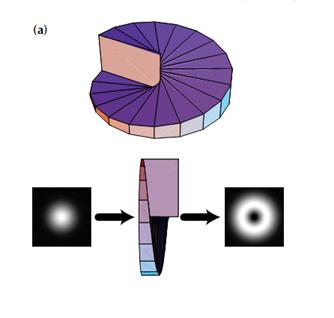
Figure 7 Using a spiral phase plate to create a vortex
Since the distance the light travels varys with the azimuthal angle, the resulting phase pattern likewise varies with the azimuthal angle.
Detecting a Vortex
We can detect the vortex using a CCD camera.
Spontaneous Formation of Vortices
In superfluid helium, when an ion is flying through the liquid, it can create vortices in its wake.
Likewise, in a Bose Einstein condensate, when there is a similar disturbance vortices are created. For example, if we create a low density line in the condensate, therefore creating a dark stripe in the condensate, then this stripe decays into vortices. And the vortices appear in vortex, anti-vortex. The behavior in BECs and light are extraordinarily similar.
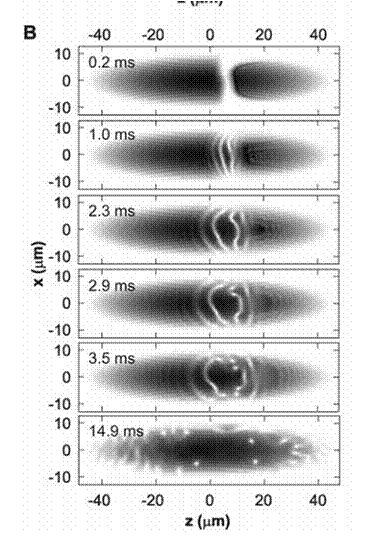
Figure 8
Spontaneous formation of vortices through the snake instability
Stability
To get a feel for the dynamics of vortices, one of the first things we need to look at is whether the vortex solution is stable or not.
As we said before, a vortex is a localized excitation that
retains its shape over time. But if the vortex is not stable under small
perturbations then in any real-life situation, the vortex will not retain its
shape. An example is shown in this picture
Here we see a bright ring vortex that is unstable. It decays into three rotating solitons. Angular momentum is conserved in the process.
Arrays
We can get a sense of the longterm behavior of vortices by looking at the minimal energy configurations. If we have a bunch of vortices, they often form an array such as those shown in the previous section because this minimizes the energy of the system.
Dynamics of a Single Vortex
In a superconductor, there are three types of forces. The
only one of these that is present in an ideal superfluid is the Lorentz force
From quantum mechanics we know that the probability current density is in the direction of the gradient of the phase. If the intensity of the background field is uniform then the dark core of the vortex will move in the opposite direction of the phase gradient. Similarly, if the phase is constant, then the vortex moves perpendicularly to the intensity gradient.
Vortex Interaction
We can use the same principle to understand vortex interaction. For example, if there are two vortices and we’re interested in the force on one of the vortices then we can consider the other vortex as a part of the background. And we know that the phase circles around a vortex. And the force on a vortex is in the direction of decreasing phase. So for two vortices, they will feel a force in the direction perpendicular to the line joining them. And so this force will motivate them to either circle around each other or move parallel to each other.
Vortex Pinning
Earlier, I mentioned that there were three types of forces in superconductors and superfluids. The second type of force is the interaction between the vortex and the normal component of the superfluid which leads to dissipation. And the third type of force is the interaction of the vortex with defects in the material which leads to vortex pinning.
A superfluid without vortices experiences no dissipation. But in a homogenous material, if vortices form then they interact with the normal component of the fluid and this leads to dissipation. This is why vortex pinning is important. If we can pin the vortex – and therefore get it out of the way – we can reduce dissipation.
Interaction Between Coherent and Incoherent; Effect of Dissipation; Effect of Defects
Many aspects of the behaviors of superfluids and superconductors can be understood using the two fluid model: they act as if they are made of a normal fluid component and a superfluid component. This model is imperfect because of the strong interactions between the particles in superfluids and superconductors, but the model is much more apropos when describing Bose Einstein condensates.
When the quantum fluid (superfluid helium, superconductor, or BEC) is above the critical temperature it behaves like a normal fluid. But once we cross the critical temperature, a portion of the fluid condenses into a coherent state. We call this portion the superfluid component. The superfluid component has no friction, dissipation, or viscosity. The uncondensed portion of the fluid is incoherent and behaves like a normal fluid. As we lower the temperature, a greater portion of the fluid becomes superfluid, while less is normal fluid. And according to the model, at absolute zero, it’s all superfluid.
A major part of understanding the behavior of quantum fluids is understanding the interaction between the superfluid component and the normal component (one of the components is coherent and the other is incoherent).
Additionally, a major aspect of condensation is the idea that a condensed quantum fluid can be described by a coherent matter wave. This is an approximation that is more accurate in the case of BECs (because they are weakly interacting) and less accurate in strongly interacting quantum fluids such as superconductors and superfluid helium.
We can use nonlinear optics to study the interaction between coherent, incoherent, and partially coherent light. And we can create vortices in light regardless of the degree of coherence.
It would be interesting (to me at least) to use nonlinear optics to gain greater insight into the interaction of the normal component and the superfluid component of superfluid helium, superconductors, and BECs, and to gain insight into the coherence of these quantum fluids. By using light we have a chance to isolate the effects of coherence in the dynamics of vortices, and we can compare the results to the behavior of vortices in the other quantum fluids.
Similarly, using light we can study the effect of dissipation by itself. Experimentally, one way that people create optical vortices that experience dissipation is by creating vortices in a cavity.
It would be interesting to see what the study of optical vortices that experience dissipation can tell us about the other quantum fluids that experience dissipation due to the interaction between the normal component and the superfluid component.
Likewise we can study the effect of defects in optical vortices to compare with the situation in the other quantum fluids. This is also important because of its relation with vortex pinning and light-guiding-light. Defects can include everything from defects in a crystal to the effect of a guiding light beam.
In light we can study each of these effects in isolation. This may allow us a chance to gain new perspectives and new insights.
Vortex Pinning and Vortex Tunneling
As mentioned earlier, vortex pinning is extremely important in superfluid helium and superconductors. We study vortex pinning in light to gain greater insight into the phenomena of vortex pinning in the other quantum fluids. Additionally, studying vortex pinning and tunneling is important because of its links to the ‘manipulation’ of vortices. ‘Manipulation’ of vortices could potentially be very important in quantum computing because of the relation between vortices and orbital angular momentum of photons. Orbital angular momentum provides a higher dimensional Hilbert space than qubits in which to do quantum computing.
Vortex pinning can be achieved in a number of ways such as the defects mentioned earlier. Of specific interest is using a second light beam to serve as the pinning mechanism. Generalizing this idea we can create a defect in an optical lattice and see the effect that this has on the guided beam. Similar work has been done in BECs. For example, people have looked at the interaction between an optical lattice and an array of vortices. This provides a good situation to compare the results done in light with the similar experiments being done in BECs.
Entanglement
Quantum vortices can become entangled. This has relevance in quantum information and quantum computing. For example, quantum vortices can be stronger violators of Bell’s inequalities, than qubits. The reason for this is that when we’re working with the orbital angular momentum of light, we have a much larger Hilbert space to work with than when we’re working with qubits. So optical vortices are of interest to quantum computing for two reasons: 1. They give us insight into superconductors and BECs, both of which are being thoroughly investigated as possible carriers of information in a quantum computer. And since the behavior of light can be so similar to the behavior of these other systems, we can use light as a simulator to predict the behavior of these other systems in definite experimental contexts. We can use light to gain a greater theoretical understanding of these systems. 2. Optical vortices also have the possibility of being the carriers of information in a quantum computer. This is not only because we can transfer information from an optical vortex to a BEC vortex coherently, but also because there are a number of all-optical possibilities.
Works Cited
Blatter, F.
G. (1994). Vortices in High Temperature superconductors. Reviews of Modern
Physics .
Courtial, &
Holleran. (2007). Experiments with twisted light. European Physical Journal
.
Desyatnikov, T. K.
(2005). Optical Vortices and Vortex Solitons. Progress in Optics .
Dutton, B. S. (n.d.).
Eilbeck, C.
Heriot-Watt university.
Engles, P.
Guenault, T. (2002). Basic
Superfluids. Taylor and Francis.
Russell, J. S. (1844).
Report of 14th Meeting of the British Association for Advancement of Science.
311-390.