Consider a region of space where there is an electric field given by:
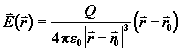
where:
![]()
![]()
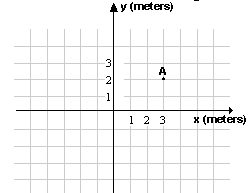
Student difficulties with math in physics: Why can’t students apply what they learn in math class?*
Richard N. Steinberg
Jeffery M. Saul
Michael C. Wittmann
Edward F. Redish
Physics Education Research Group
University of Maryland
* sponsored in part by NSF grants RED-9355849 and DUE-9455561
For the companion talk by Edward F. Redish, see "Student difficulties with math in physics: Giving meaning to symbols"
Context for this research
Methods of investigation
How do students interpret and apply mathematics in introductory physics?
Students need facility with many mathematical representations in learning introductory physics:
Graphs
Equations
Vectors
Example from electrostatics Midterm Examination (N=95)
Consider a region of space where there is an electric field given by:
where:
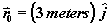
Part A: Determine the value of E at the point labeled A.
Part B: Draw electric field lines for this region of space.
Example from mechanical waves
Pretest (N=57) Individual interviews (N=9)
Consider the pulse below at t = 0 moving in the x direction with velocity vo.
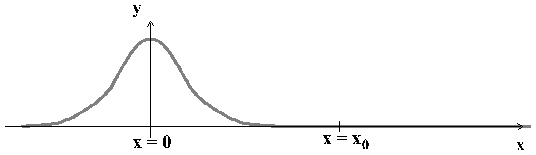
The displacement of the spring from its equilibrium position at t = 0 is given by:
Part A: Sketch the shape of the spring after it has traveled a distance xo.
a correct response (pulse displaced, amplitude unchanged)

pretest: 56%; interview: 44%
correct response? (pulse displaced, amplitude decreased)
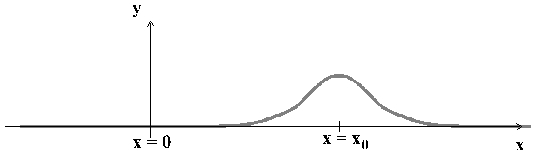
pretest: 35%; interview: 56%
Part B: Write an equation for y as a function of x when the pulse reaches xo.
Summary
Students have difficulty interpreting and applying mathematical ideas when learning introductory physics.
In the context of equations:
Research-based curriculum
Students, working independently, make predictions about a propagating pulse and its mathematical form.
Students, working in groups:
This page prepared by:
Richard Steinberg
University of Maryland
Physics Department
College Park, MD 20742-4111
(301) 405-6184