1) Some of the graphs shown below represent the motion of a pendulum
-- a massive ball attached to a rigid, nearly massless rod, which in turn
is attached to a rigid, nearly frictionless pivot.
On the right below are shown four graphs of the pendulum's angle as
a function of time. On the left are a set of four initial conditions and
a denial. Match each graph with its most likely initial conditions (or
with the denial). Note that the scales on the y axes are not necessarily
the same. (There is not necessarily a one-to-one match.)
| (1) q0 = 120o w0
= 0
(2) q0 = 173o w0
= 30o/s
(3) q0 = 6o w0
= 0
(4) q0 = 173o w0
= 0
(5) Not a possible pendulum graph.
|
(A) 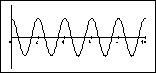 (B) (B) 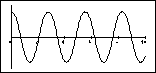
(C) 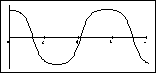 (D) (D) 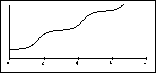
|
2) A pendulum consisting of a massive ball on a light but nearly rigid
rod is shown at three successive times in the pictures on the below. The
maximum angle of displacement of the pendulum from its equilibrium point
is 90o.
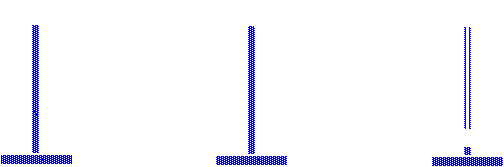
Copy each of the pictures. On each picture draw three arrows indicating
the direction of
_ the mass's velocity (a single arrow like
this: ->;
_ the total force the mass feels (a double arrow
like this: =>; and
_ the acceleration of the mass (a boldface arrow
like this:  ).
).
3) This problem uses the M.U.P.P.E.T. program Pendulum*.
The pendulum satisfies the equation of motion derived in class
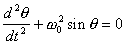
(assuming no damping). We will refer to this as the exact equation.
It has to be solved numerically. (This is what the program Pendulum
does.) For small angles we can approximate sinq
by q. This gives the equation for simple harmonic
motion 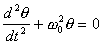
which we can solve analytically. We refer to this as the approximate
equation.
(a) In the program Pendulum, set the starting angle to 15o
, the starting velocity and the damping to 0. Look at the curves for the
position, velocity, and acceleration of the bob. Do they resemble each
other? Do they look like simple harmonic motion? Why?
(b) Increase the starting angle to 180o in steps of 15o.
(Do not actually use 180o. It will crash the program. Use 179o.)
At each step, read the period from the graph. Try to get two significant
figures. Plot the period as a function of starting angle. (It might be
easier to read if you start with x0 = 0 and v0 >
0.)
(c) Describe what happens to the velocity curve as the angle approaches
180o. At what angle does it begin to differ visibly from the
harmonic oscillator curves?
(d) Qualitatively compare what the "exact" and "approximate"
results look like for the initial conditions
q(t=0) = 3.0 rad, 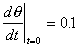 rad/sec;
rad/sec;
q(t=0) = 6.0 rad, 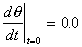 rad/sec.
rad/sec.
Describe what is happening physically in the two cases. Why is there
a qualitative difference between the results in the two methods?
4) Consider a pendulum of mass m and length L.
(a) Derive the energy conservation equation for the motion of the pendulum.
(Do not use the small amplitude approximation.)
(b) If the pendulum is released from a starting angle of q0,
what will be the maximum speed it travels at any point on its swing?
| (c) When on vacation this summer, I visited a forest which
had many waterfalls. At one of the waterfalls, a long rope hung down from
the top of the cliff near the waterfall and had a seat on the bottom. Adventurous
visitors could hop onto the seat and swing down into the waterfall as shown
in the photo at the right. I estimated that their starting angle was about
20o. I also timed their swing and discovered it took them 8
seconds to swing out and back. Estimate the length of the rope and the
speed with which they passed through the waterfall. (The top of the rope
is not shown in the photo.) |
 |
5) A small metal ball of mass m hangs from a pivot by a rigid, light
metal rod of length R as shown in the figure on the right. The ball is
swinging back and forth with an amplitude that remains small throughout
its motion (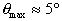 ).
Ignore all damping.
).
Ignore all damping.
(a) The equation of motion of this ideal pendulum can be derived in
a variety of ways and is 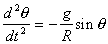 .
.
For small angles, show how this can be replaced by an approximate equation
of motion that can be solved more easily than the one given.
(b) Write a general solution for the approximate equation of motion you
obtained above that works for any starting angle and angular velocity (as
long as the angles stay in the range where the approximation is OK). Demonstrate
that what you have written is a solution and show that at a time
t=0 your solution can have any given starting position and velocity.
(c) If the length of the rod is 0.3 m, the mass of the ball is 0.2 kg,
and the clock is started at a time when the ball is passing through the
center (q = 0) and is moving with an angular
speed of 0.1 rad/s, find the maximum angle your solution says the ball
will reach. Does the approximate equation of motion remain valid for this
motion?


 (B)
(B) 
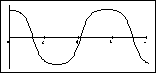 (D)
(D) 

![]() ).
). ![]()
![]()
![]() rad/sec;
rad/sec;![]() rad/sec.
rad/sec. 
![]() ).
Ignore all damping.
).
Ignore all damping. ![]() .
.