2) Observation of a mass on the end of a spring reveals that the detailed
structure of the position as a function of time is fit very well by a function
of the form x(t) = A cos(wt + f).
Yet subsequent observations give convincing evidence that this cannot be
a good representation of the motion for long time periods. Explain what
observation leads to this conclusion and resolve the apparent contradiction.
| 3) A block of mass m is attached to a spring of spring constant k which
is attached to a wall as shown on the right. |
 |
(a) If the block starts at time t=0 with the spring being at its rest
length but the block having a velocity v0, find a solution for
the mass's position at all subsequent times. Make any assumptions you like
in order to have a plausible but solvable model, but state your assumptions
explicitly.
(b) Are the energies at the times
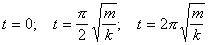
kinetic, potential, or a mixture of the two? (This is not a short
answer question. Show how you know.)
4) A class looked at the oscillation of a mass on a spring. They observed
for 10 seconds and found its oscillation was well fit by assuming the mass's
motion was governed by Newton's second law with the static-spring force 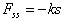 where s represents the stretch of the spring. However, it was also
clear that this was not an adequate representation for times on the order
of 10 minutes, since by that time the mass had stopped oscillating.
where s represents the stretch of the spring. However, it was also
clear that this was not an adequate representation for times on the order
of 10 minutes, since by that time the mass had stopped oscillating.
(a) Suppose the mass was started at an initial position x0
with a velocity 0. Write down the solution, x(t) and v(t), for the equations
of motion of the mass using only the static-spring force. What is the total
energy of the oscillating mass?
(b) Assume that there is also a velocity dependent force (the damping
force) that the spring exerts on an object when it is moving. Let's make
the simplest assumption, that the dynamic-spring force is linear in the
velocity 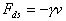
Assume further that over one period of oscillation the velocity dependent
piece is small. Therefore, take x(t) and v(t) to be given by the oscillation
without damping. Calculate the work done by the damping force over one
period in terms of the parameters k, m, and g
and the fraction of the energy lost in one period.
(c) The mass used was 1 kg. From the description of the experiment, estimate
the spring constant and the number of periods it took to lose half the
energy. Use this and your result from (a) to estimate the approximate size
of the damping constant g.
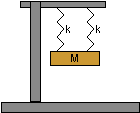
| 5) A mass, m, hangs from two identical springs with
spring constant k which are attached to a heavy steel frame as shown
in the figure on the right.
(a) If the system is at rest, what is the distance s0
that each spring is stretched?
(b) Suppose the mass is at a position which is a distance x above
its equilibrium point. Identify all the forces acting on the mass and the
net force acting on the mass. (Assume the mass remains doesn't tilt.)
(c) Write the equation of motion for the motion of the mass and show that
it is the same as one would have if one hung the mass from a single spring
of spring constant keff and find the value of keff.
(d) Write the solution to the equation of motion for the mass for the case
that the mass is started at time t = t0 with a position
x0 and a velocity 0.
|
 |
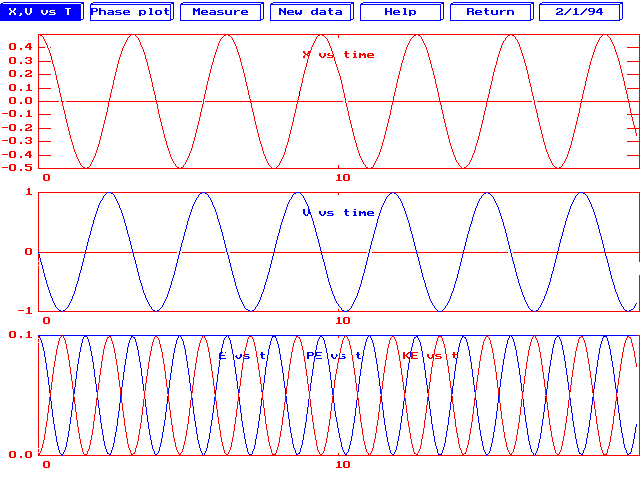
6) The graphs at right represent a computer simulation of
a mass on a spring. The kinetic, potential, and total energy were plotted
as well as the position and velocity of the oscillator.
(Graphs generated by use of the program HARMOSC
*.
The potential and kinetic energy curves oscillate, but not about zero.
They also seem to oscillate twice as fast as the position and velocity
curves. Is this correct? Explain.
|
 |
7) Solving the equation of motion of a mass hanging from a spring, we
obtain the solution x[t] = A cos wt.
If an actual mass is hung from a spring and data is taken using a sonic
ranger, two problems are observed: the displacement curve does not start
at its maximum value, and the oscillation diminishes over time. Discuss
what was the difficulty with our mathematical model of the system and how
you would fix the two problems.
8) As a lecture demonstration, a Professor starts a mass on a spring
oscillating. After a few minutes, the oscillation died down. The mass used
had a mass of M = 50 grams, the spring had a spring constant of
k = 5 Newtons/meter and the spring had a mass of m = 5 grams.
Estimate the rise in temperature of the spring. State clearly all the numbers
you are estimating and begin with a few sentences explaining what physical
principles will be relevant in carrying out your calculation.
9) A 50 gram mass is hanging from a spring whose unstretched length
is 10 cm and whose spring constant is 2.5 N/m.
In the list below are described five situations. In some of the situations,
the mass is at rest and remains at rest. In other situations, at the instant
described, the mass is in the middle of an oscillation initiated by a person
pulling the mass downward 5 cm from its equilibrium position and releasing
it. Ignore both air resistance and internal damping in the spring.
At the time the situation occurs, indicate whether the force vector
requested points up (U), down (D), or has magnitude zero (0).
(a) The force on the mass exerted by the spring when the mass is at
its equilibrium position and is at rest.
(b) The force on the mass exerted by the spring when the mass is at its
equilibrium position and is moving downward.
(c) The net force on the mass when the mass is at its equilibrium position
and is moving upward.
(d) The force on the mass exerted by the spring when it is at the top of
its oscillation.
(e) The net force on the mass when it is at the top of its oscillation.
10) In a nucleus that undergoes nuclear fission, the parts of the nucleus
repel each other because they all have the same electric charge, but attract
each other because of the strong nuclear force. Let's start on building
up a model of a nucleus that consists of two (reasonably) small particles
of mass m, that each have a charge q, and that are connected
by a spring of spring constant k. Let's also assume that the spring
has a rest length of 0.

(a) What will be the equilibrium separation, L, between the two
charges? Express your answer in terms of the given parameters of the system.
(b) What will the total potential energy of the system be at equilibrium?
Express your answer in terms of the given parameters of the system and,
if necessary, universal constants.
| 11) One end of a spring is attached to a wall, and the other
to a cart as shown in the figure below. When the marker on the cart is
at x=0 the spring is relaxed -- neither compressed nor stretched. The cart
has a mass of 250 g, the rest length of the spring is 6 cm and it has a
spring constant k = 0.5 N/cm. The cart is grabbed and pulled to the right
a distance of 2 cm and held there.
(a) What forces are felt by the spring? Be sure to identify the
type of force and the agent causing it in each case. What is the total
force on the spring?
(b) What forces are felt by the cart? Be sure to identify the type
of force and the agent causing it in each case. What is the total force
on the cart?
(c) If the cart is released, with what period will it oscillate?
|
 |
12) The following problem is found in Halliday and Resnick's Fundamentals
of Physics, a popular introductory text.
A block of mass M at rest on a horizontal frictionless table. It is
attached to a rigid support by a spring of constant k. A bullet of mass
m and velocity v strikes the block as shown in the figure. on the next
page. Determine (a) the velocity of the block immediately after the collision
and (b) the amplitude of the resulting simple harmonic motion.
In order for you to solve this problem you must make a number of simplifying
assumptions, some of which are stated in the problem and some of which
are not. First, solve the problem as stated. Then (c) discuss the approximations
which you had to make in order to solve the problem. I can think of at
least five.
| 13) Two springs are joined and connected to a mass m as shown in the
figure below. The surfaces are frictionless.
(a) If the force constants of the springs are k1 and k2,
what is the frequency of the mass's oscillation? (Hint: Write the
equation of motion for the mass after writing free body diagrams for each
spring and for the mass.)
(b) What is the "effective spring constant" of the combination
of k1 and k2? (That is, if the mass were hooked to
a single spring, for what value of k would it have the same frequency as
we have here?)
|
 |
14) A mass m on a spring with spring constant k is started at time t
= 0 with a velocity v0 at position x0 = 0.
(a) Assuming no damping, what is the equation of motion the position
of the mass satisfies?
(b) Find an explicit general solution x(t) that satisfies this equation
for any initial conditions.
(c) Find a particular solution that satisfies the initial conditions given.
Demonstrate that for your solution x(0) = x0 = 0 and v(0) =
v0.
(d) For the particular case discussed here, what is the initial energy
of the oscillator?
(e) Are the energies at the times 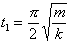 ,
, 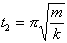 ,
, 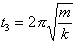 kinetic, potential, or a mixture of the two? (This is not a short
answer question. Show how you know.)
kinetic, potential, or a mixture of the two? (This is not a short
answer question. Show how you know.)
| 15) As part of a Physics Open House a Department sets up
a bungee jump from the top of their physics building. Assume that one end
of an elastic band will be firmly attached to the top of the building and
the other to the waist of a courageous participant. The participant will
step off the edge of the building to be slowed and brought back up by the
elastic band before hitting the ground (we hope). Estimate the length and
spring constant of the elastic you would recommend using. |

Picture Courtesy of
Atti Laurila |
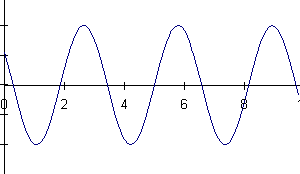
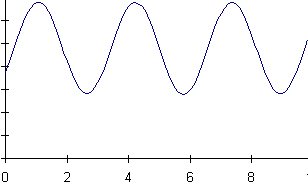
16) A mass is hanging from a spring off the edge of a table. The position
of the mass is measured by a sonic ranger sitting on the floor 25 cm below
the mass's equilibrium position. At some time, the mass is started oscillating.
At a later time, the sonic ranger begins to take data.
Below are shown a series of graphs associated with the motion of the
mass and a series of physical quantities. The graph labeled (A) is a graph
of the mass's position as measured by the ranger. For each physical quantity
identify which graph could represent that quantity for this situation.
If none are possible, answer N.
a) velocity of the mass b) net force on the mass
c) force exerted by the spring on the mass d) kinetic energy of the mass
e) potential energy of the spring f) gravitational potential energy of
the mass
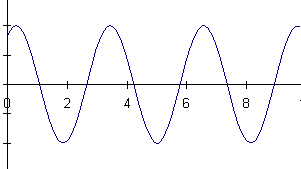
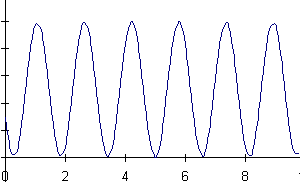
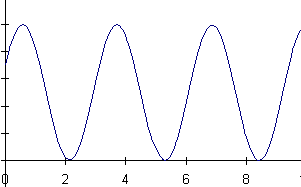
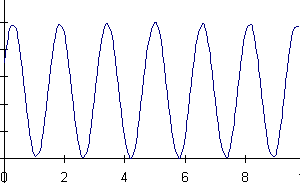




![]()
![]() where s represents the stretch of the spring. However, it was also
clear that this was not an adequate representation for times on the order
of 10 minutes, since by that time the mass had stopped oscillating.
where s represents the stretch of the spring. However, it was also
clear that this was not an adequate representation for times on the order
of 10 minutes, since by that time the mass had stopped oscillating.
![]()






![]() ,
, ![]() ,
, ![]() kinetic, potential, or a mixture of the two? (This is not a short
answer question. Show how you know.)
kinetic, potential, or a mixture of the two? (This is not a short
answer question. Show how you know.) 






![]()