
 |
Activity Based Physics Thinking Problems in Mechanics: Universal Gravitation |
1) Someone once stopped me in the hall and said: "I can prove Newton's
theory of gravity is wrong. The sun is 320,000 times as massive as the
earth, but only 400 times as far from the moon as the earth is. Therefore
the force of the sun's gravity on the moon should be twice as big as the
earth's and the moon should go around the sun instead of around the earth.
Since it doesn't, Newton's theory of gravity must be wrong!" What's
the matter with this reasoning? 2) The next problem uses the computer program ORBITS *. Run ORBITS and select the scenario SPSTATN (Space Station). This features
a space ship in the same circular geosynchronous as a space station. Unfortunately,
it is in orbit one-fourth of an orbit behind a space station. You want
to rendezvous with the station by matching position and velocity with it.
Try to rendezvous with the station by adding or subtracting velocity
(thrust) to your space ship using the + key to control the amount of thrust
and the arrow keys on the numeric keypad to control the direction (of Dv).
Try a variety of procedures before choosing a final one. When you have
decided on a procedure, perform it and write down what you did and the
total amount of thrust you used. You can reset the program to the starting
values by pressing <esc> and selecting SPSTATN again. (Hint:
A rendezvous can be achieved using only 2 thrusts.) To view how closely you've rendezvoused, when you are satisfied, press<Ctrl><F2>
to record your final positions and velocities to the data tables. Return
to the data tables by pressing <BACKSPACE>. Press <PrtSc> to
print out the exact values of the x and y positions and the x and y velocities
of the space ship and space station. Calculate your distance from the space
station and the relative velocity between you and the space station using
the Pythagorean theorem. 3) The orbiting Hubble telescope was recently repaired by a crew of
astronauts from the Space Shuttle Endeavor. The Hubble is in a circular
orbit 600 km above the surface of the earth. For half of the Hubble's orbital
period it is in sunlight and for half it is in the darkness of the earth's
shadow. As a result of the change in fit of the various parts of the Hubble
due to heating and cooling of the telescope, the astronauts could only
work on certain repairs while the Hubble was in darkness. Estimate how
much time the astronauts had to work on these repairs before having to
stop "for a sun-break". (a) On a copy of the figure on your paper, draw vectors representing Draw your vectors so that each type of vector can be distinguished.
Be sure to give a legend that shows how each type is being represented.
5) Suppose you are piloting the space ship in the problem above and
that the point at A is at a distance of 3 earth radii from the earth's
surface, and the point B is at a distance of 1 earth radius from the center.
You are at point A and want to change your orbit. (a) What would happen to the shape of your orbit if you decided to speed
up in the direction you are heading by firing your aft rockets briefly? 6) Two schoolmates, Romeo and Juliet, catch each other's eye across
a crowded dance floor at a school dance. Estimate the gravitational attraction
they exert on each other. * This software may be obtained from Physics
Academic Software These problems written and collected by E. F. Redish. These problems
may be freely used in classrooms. They may be copied and cited in published
work if the Activity Based Physics Thinking Problems in Physics site
is mentioned and the URL given. Web page edited by K.A. Vick. To contribute problems to this site, send them to redish@physics.umd.edu.
Maintained by
University of Maryland PERG
Activity Based Physics Thinking Problems in Mechanics: Universal Gravitation
4) On the figure at the right is shown a space ship going in an elliptical
orbit around the earth. Take the origin of your coordinate system to be
at the center of the earth.
(b) Have you drawn the velocity vector at A longer, shorter, or the same
length as the one at B? Explain why.
(c) Have you drawn the acceleration vector at A longer, shorter, or the
same length as the one at B? Explain why you have done so.
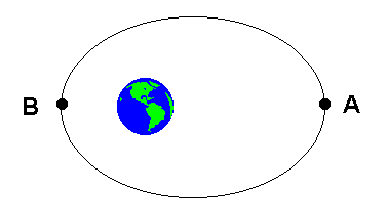
(b) What would happen to the shape of your orbit if you decided to slow
down in the direction you are heading by firing your fore rockets briefly?
(c) If you want to put yourself into a circular orbit passing through the
point A, how would you do it? (Be quantitative!)
Go back to the Activity Based Physics page
Go back to the Thinking Problems page
Go back to the Thinking Problems in Mechanics page
![]()
Comments and questions may be directed to
E. F. Redish
Last modified June 21, 2002