4) Sketch qualitatively the pattern of electric field lines created
by four equal positive charges placed at the corner of a square. Sketch
qualitatively the equipotential surfaces for this configuration. (You only
need to draw the field and potentials in the plane of the charge. Hint:
Use symmetry!)
5) (a) Suppose that I have a conducting sphere of radius R with a charge
q. Show that if I bring a small amount of charge dq from infinity up to
the surface of the sphere, that it takes an amount of work dW = Kq dq/R.
(b) Suppose I have a conducting sphere of radius R with a total charge
Q. Show that the amount of work needed to bring up all the charge on the
sphere is equal to the energy stored in the field of the sphere when it
is considered as a capacitor.
6) Two copper spheres of radius 1cm are supported on rigid insulating
rods so that their centers are a distance 100 cm apart. A charge of 0.1
mC is placed on one of the spheres
(a) What is the potential difference between the two spheres?
(b) What is the electrostatic potential energy of interaction between the
two spheres? (Assume the radii of the spheres can be considered to be negligible.)
(c) What is the total electrostatic potential energy of the system? (Now
include the energy due to the charge distribution on the one sphere. Do
not ignore the radius.)
(d) A wire is used to connect the two spheres. After a while the wire is
removed. What will be the charge on each sphere?
(e) Calculate the total electrostatic potential energy of the system now,
including the energy of interaction between the spheres and the electrostatic
potential energy stored as a result of the charge on each sphere.
(f) Why are the two energies you calculated in (c) and (e) not equal? Where
did it go?
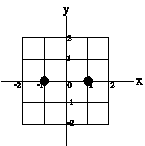
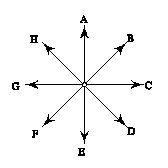
7) In the figure on the left below is displayed a grid with coordinates
measured in meters. On the grid two charges are placed with their positions
indicated as black circles. We call the charge at the position (1,0) q1,
and the charge at the position (-1,0) q2.
In the middle figure below is displayed a set of possible vector directions.
On the right is a list of the components of possible E fields. For each
of the three cases described below specify: an arrow corresponding to the
directions of the E field from the middle figure, and a set of components
from the list on the right. Each of your answers should consist of a capital
letter and a small letter.
(a) 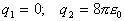 E
field at the point (x,y) = (-1,1)
E
field at the point (x,y) = (-1,1)
(b) 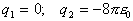 E field
at the point (x,y) = (-1,-1)
E field
at the point (x,y) = (-1,-1)
(c) 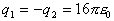 E field
at the point (x,y) = (0,-1)
E field
at the point (x,y) = (0,-1)
8) In the Millikan oil drop experiment, an atomizer (a sprayer with
a fine nozzle) is used to introduce many tiny droplets of oil between two
oppositely charged parallel metal plates. Some of the droplets pick up
one or more excess electrons. The charge on the plates is adjusted so that
the electric force on the excess electrons exactly balances the weight
of the droplet. The idea is to look for a droplet that has the smallest
electric force and assume that it has only one excess electron. This lets
the observer measure the charge on the electron. Suppose we are using an
electric field of 3x104 N/C. The charge on one electron is about 1.6x10-19
C. Estimate the radius of an oil drop for which its weight could be balanced
by the electric force of this field on one electron.
9) Define and discuss what we mean by an electric field.
10) A large sheet of plastic of dimensions LxL is charged with a uniformly
distributed charge Q. If we approximate the sheet by an infinite plane,
we can calculate the electric field it produces.
(a) Assuming we are close enough to the surface to treat the plane as
infinite, in what direction does the E field point when observed a distance
d above the plane? A distance d below the plane? Explain why you chose
the directions you did.
(b) Find E(d), the magnitude of the E field a distance d above the plane,
using Gauss's law. Express your answer in terms of the givens in the problem.
(You may also invoke universal constants.)
(c) Suppose I have two large parallel plates of charge separated by a distance
s. If the charges on the two plates are equal and opposite, use your results
in (a) and (b) to derive the field that would be found in all regions of
space.
| 11) Two equal and opposite charges are placed a small distance d apart
as shown in the figure below.
(a) On two separate copies of the figure sketch the electric lines of
force, and equipotential surfaces for this problem.
(b) Calculate the electrostatic potential for this system along the x axis.
Take your reference point to be at infinity.
(c) As x gets large compared to d, show that this potential goes to zero
more quickly than the potential for a point charge.
(Hint: You may find the following relations useful.
For any small number e,
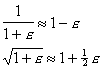
|
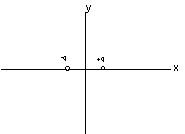 |
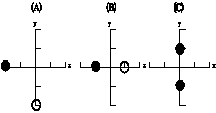
| 12) In the figures on the left below (labeled (A), (B), and (C)) are
displayed three different charge configurations on a coordinate system.
The filled in circles represent a positive charge and the open circles
represent a negative charge. All of the charges have the same magnitudes.
Each tick mark on an axis of a coordinate system represents one unit.
To the right of these pictures is a set of vectors representing different
directions.
Copy the table below the pictures. For each situation requested, fill
in a number from 1 to 8 representing the arrow that is closest to
the direction of the field at that point in the chosen configuration. For
example, in the row labeled "field at (0,0)" and the column labeled
"(B)" place a number specifying the vector which gives the direction
of the field at the point (0,0) in the picture (B). In any of the cases
if the field is zero, place the number 0.
|
|
|
|
| field at (0,0) |
|
|
|
| field at (2,0) |
|
|
|
|
|
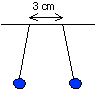
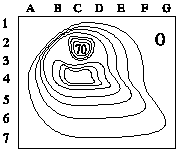
| 13) Two hard rubber spheres of mass ~ 10 g are rubbed vigorously with
fur on a dry day. They are then suspended from a rod with two insulating
strings. They are observed to hang at equilibrium as shown in the figure
on the right, which is drawn approximately to scale. Estimate the amount
of charge that is found on each sphere. |
 |
14) A system of electrified objects is arranged with some conductors
and some insulators, some being charged, others being neutral. The system
is observed at a particular instant in time. In this context, explain what
is meant by the electrostatic potential V(r).
15) Three charges q1, q2, and q3 are
placed at the points represented by the vectors r1, r2,
and r3 respectively.
(a) Write an expression for the electric-field arising from these three
charges at an arbitrary point represented by the vector r.
(b) Write an expression which yields the force that charge q3
feels as a result of the presence of charges q1 and q2.
(c) If the charges have magnitudes , and are placed at the locations find
the coordinates of the vector that represents the force felt by the charge
q3.
(d) If q1 and q2 are as in part (c) but q3=0,
find the potential at an arbitrary point (0,y) along the y axis.
| 16) A long thin cylindrical shell of length L and radius R is uniformly
covered with a charge Q.
(a) If we look for the field near to the cylinder somewhere about the
middle, we can treat the cylinder as if it were infinitely long. Using
this assumption, calculate the magnitude and direction of the field at
a point a distance d from the axis of the cylinder (outside the cylindrical
shell, i.e., d > R) using Gauss's Law.
(b) Under the same approximation use Gauss's law to find the field inside
the shell.
(c) Sketch the equipotential surfaces for this object as they would appear
on a plane slicing through the cylinder lengthwise. (Let the x-axis of
the plane be the axis of the cylinder.) Let the portion of the plane you
are showing be much larger than the object. (Careful: This is the
opposite approximation from the one used in parts (a) and (b)!)
|
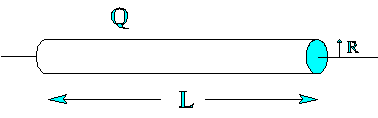 |
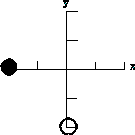
| 17) The picture on the right displays two charges placed on a coordinate
grid. Each of the tic marks on the axes represents 1 m. The magnitude of
the charge represented by the solid circle is q1
and is at the position (-2,0), while the charge represented by the
open circle is q2 and is at the
position (0,-2). |
 |
On the left below is a list of four sets of configurations specifying
the value of the charges and a positions at which the E field is to be
measured. On the right is a list of twelve possible electric fields represented
as x-y components. For each of the four configurations select the E-field
components which represent the field that would be found at that position.
| Configuration |
|
|
q1 |
q2 |
Position |
| 17.1 |
16pe0 |
-16pe0 |
(0,0) |
| 17.2 |
16pe0 |
-16pe0 |
(-2,-2) |
| 17.3 |
16pe0 |
0 |
(0,0) |
| 17.4 |
0 |
-16pe0 |
(-2,-2) |
|
| (a) (1, 0) |
(g) 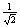 (1,
-1) (1,
-1) |
| (b) (0, -1) |
(h) 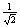 (-1,
1) (-1,
1) |
| (c) (1, -1) |
(i) 2 (1, 0) |
| (d) (-1, 0) |
(j) 2 (0, 1) |
| (e) (-1, 1) |
(k) 2 (-1, 0) |
| (f) (0, 1) |
(l) 2 (0, -1) |
|
18) Gauss's law is usually written as an equation in the form 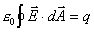 .
.
(a) For this equation, specify what each term in this equation means
and how it is to be calculated when doing some specific (but arbitrary
- not a special case!) calculation.
A long thin cylindrical shell of length L and radius R with L>>R
is uniformly covered with a charge Q. If we look for the field near to
the cylinder somewhere about the middle, we can treat the cylinder as if
it were an infinitely long cylinder. Using this assumption, we can calculate
the magnitude and direction of the field at a point a distance d from the
axis of the cylinder (outside the cylindrical shell, i.e., L>>d
> R but d not very close to R) using Gauss's Law. Do so by explicitly
following the steps below.
(b) Select an appropriate Gaussian surface. Explain why you chose it.
(c) Carry out the integral on the left side of the equation, expressing
it in terms of the unknown value of the magnitude of the E field.
(d) What is the relevant value of q for your surface?
(e) Use your results in (c) and (d) in the equation and solve for the magnitude
of E.
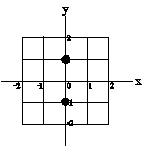
19) In the figure on the left below is displayed a grid with coordinates
measured in meters. On the grid two charges are placed with their positions
indicated as black circles. The charge q1
is at the position (0,1), and the charge q2
is at the position (0, -1). In the middle figure below is displayed a set
of possible vector directions. On the right is a list of the components
of possible E fields.
For each of the three cases described below specify: an arrow corresponding
to the directions of the E field from the middle figure and a set of components
from the list on the right. Each of your answers should consist of a capital
letter and a small letter. (K stands for the Coulomb force constant, often
written 1/4pe0.)
(a) 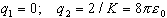 E field at the point (x,y) = (1,-1)
E field at the point (x,y) = (1,-1)
(b) 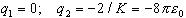 E field
at the point (x,y) = (-1,-1)
E field
at the point (x,y) = (-1,-1)
(c) 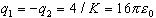 E field
at the point (x,y) = (-1,0)
E field
at the point (x,y) = (-1,0)
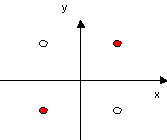
| 20) In the figure at the right is shown a set of 4 charges and a coordinate
system. The charges at (1,1) and (-1,-1) are positive, while the ones at
(-1,1) and (1,-1) are negative.
(a) Copy the picture and draw vectors indicating the electric field
a test charge would see if it measured the electric force along the x and
y axes.
(b) Sketch a graph of the electric potential along the x axis.
(c) Copy the picture a second time and sketch on it equipotentials and
lines of force.
|
 |
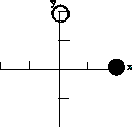
| 21) The picture on the right displays two charges placed on a coordinate
grid. Each of the tic marks on the axes represents 1 m. The magnitude of
the charge represented by the solid circle is q1
and is at the position (2,0), while the charge represented by the open
circle is q2 and is at the position
(0,2). |
 |
On the left below is a list of 5 sets of configurations specifying the
value of the charges and a positions at which the E field is to be measured.
For ease of calculation, these are represented in terms of the Coulomb
constant K = 1/4pe0. On the right
is a list of twelve possible electric fields represented as x-y components.
For each of the four configurations select the E-field components which
represent the field that would be found at that position.
| Configuration |
|
|
q1 |
q2 |
Position |
| 21.1 |
4/K |
-4/K |
(0,0) |
| 21.2 |
4/K |
-4/K |
(2,2) |
| 21.3 |
4/K |
0 |
(0,0) |
| 21.4 |
0 |
-8/K |
(-2,2) |
|
| 21.5 |
0 |
-8/K |
(2,0) |
|
| (a) (1, 0) |
(g) 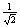 (1,
-1) (1,
-1) |
| (b) (0, -1) |
(h) 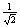 (-1,
1) (-1,
1) |
| (c) (1, 1) |
(i) 2 (1, 0) |
| (d) (-1, 0) |
(j) 2 (0, 1) |
| (e) (-1, 1) |
(k) 2 (-1, 0) |
| (f) (0, 1) |
(l) none of the above |
|
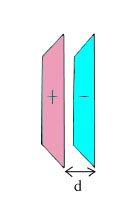
| 22) In the figure on the right are shown two large parallel
sheets of charge separated by a distance d, small compared to the size
of the sheets. The distance d is small enough that the sheets can be treated
as if they were infinite in extent. The amount of charge per unit area
in the sheets are +s and -s
respectively.
(a) What is the electric field between the two sheets and outside the
two sheets?
(b) What is the electrostatic potential difference between the two sheets?
(c) An uncharged conducting slab of thickness d/2 is inserted between the
two sheets of charge but does not touch either of them. Describe the charge
densities and electric fields everywhere in the system once everything
has settled down and charges have stopped moving.
(d) What is the electrostatic potential difference between the two sheets?
|
 |
23) The next two questions concern general applications of Gauss's Law.
Gauss's law states 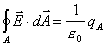
where A is a surface and qA is a charge. (Note: You
may list any number of these statements including all or none. Points will
be subtracted for wrong answers.)
23.1. Which of the following statements are true about the surface A
appearing in Gauss's Law?
a. The surface A must be a closed surface (must cover a volume).
b. The surface A must contain all the charges in the problem.
c. The surface A must be a highly symmetrical surface like a sphere or
a cylinder.
d. The surface A must be a conductor.
e. The surface A is purely imaginary.
f. The normals to the surface A must all be in the same direction as the
electric field on the surface.
23.2. Which of the following statements are true about the charge qA
appearing in Gauss's Law?
a. The charge qA is all the charge lying on the Gaussian
surface.
b. The charge qA is the charge lying within the Gaussian surface.
c. The charge qA is all the charge in the problem.
d. The charge qA flows onto the Gaussian surface once the surface
is established.
e. The electric field E in the integral on the left of Gauss's law is due
only to the charge qA.
f. The electric field E in the integral on the left of Gauss's law is due
to all charges in the problem.
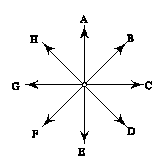
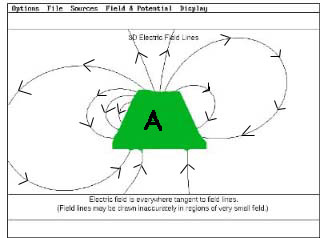
24) The next four problems refer to the two figures below. In these
figures are shown some representative electric field lines associated with
some charges. Both pictures show the same charges and field lines, but
they are masked in different ways by imaginary closed surfaces drawn for
the purpose of hiding the charges from your view.
| 24.1. From the field lines in the two pictures, which of
the following statements is most likely to be true.
a. There are no charges contained in A.
b. The charge contained in A is positive.
c. The charge contained in A is negative.
d. The total charge contained in A is zero.
e. None of the above can be true.
24.2. From the field lines in the two pictures, which of the following
statements is most likely to be true.
a. There are no charges contained in B.
b. The charge contained in B is positive.
c. The charge contained in B is negative.
d. The total charge contained in B is zero.
e. None of the above.
|
 |
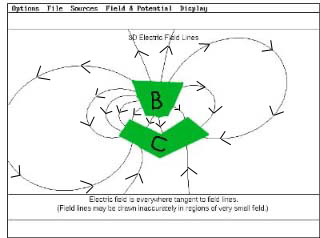
| 24.3. From the field lines in the two pictures, which of the following
statements is most likely to be true.
a The charge contained in C is positive and greater in magnitude than
the charge in B.
b. The charge contained in C is positive and smaller in magnitude than
the charge in B.
c. The charge contained in C is negative and greater in magnitude than
the charge in B.
d. The total charge contained in C is negative and smaller in magnitude
than the charge in B.
e. None of the above.
24.4. From the information in the two pictures, what can you say about
the electrostatic potential at a point on the surface of box B compared
to the electrostatic potential on the surface of box C?
a. The potential of any point on the surface of B is higher than the
potential of any point on the surface of C.
b. The potential of any point on the surface of C is higher than the potential
of any point on the surface of B.
c. The potential on the surface B and C are the same.
d. Some of the points on B will be at a higher potential than some of the
points on C, but not all of them.
e. Nothing can be determined about the relative potentials.
|
 |
25) Consider a spherical charge distribution which has a constant density
r from r = 0 out
to r = a and is zero beyond. Find the electric
field for all values of r, both less than and
greater than a. Is there a discontinuous change in the field as we pass
the surface of the charge distribution at r =
a? Is there a discontinuous change at r = 0?



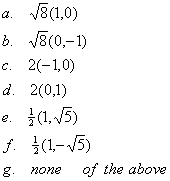
![]() E
field at the point (x,y) = (-1,1)
E
field at the point (x,y) = (-1,1) ![]() E field
at the point (x,y) = (-1,-1)
E field
at the point (x,y) = (-1,-1) ![]() E field
at the point (x,y) = (0,-1)
E field
at the point (x,y) = (0,-1) 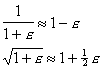
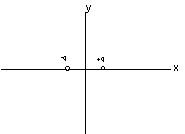



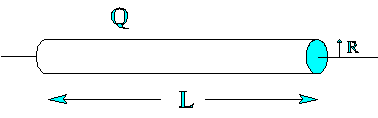

![]() (1,
-1)
(1,
-1) ![]() (-1,
1)
(-1,
1) ![]() .
.
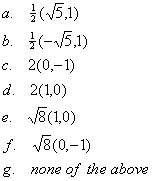
![]() E field at the point (x,y) = (1,-1)
E field at the point (x,y) = (1,-1) ![]() E field
at the point (x,y) = (-1,-1)
E field
at the point (x,y) = (-1,-1) ![]() E field
at the point (x,y) = (-1,0)
E field
at the point (x,y) = (-1,0) 

![]() (1,
-1)
(1,
-1)![]() (-1,
1)
(-1,
1)
![]()


![]()