
 |
Alternative Homework Assignment: Rocket Motion |
 |
Problem #1In order to study the ozone layer, it is important to get instruments into this level of atmosphere. One method of doing this is to place the instruments in a rocket that lifts the instruments to the top of the ozone layer (48,000 m) and lets them parachute back down to earth. Such a rocket might have to carry a 10 kg payload. In the following calculations, assume that the rocket's fuel has negligible mass and that the accelerations are constant. Also assume that air friction is negligible. a) There are two important stages to consider in the rocket's ascent. The rocket will speed up while its engine is firing, and then slow down after the engine has shut off. If it reaches a maximum velocity of 600 m/s, how far upward does it travel after the engine is out of fuel? b) From the above result, it is possible to calculate how far the rocket traveled while using the engine. Use this result and the maximum velocity to calculate the acceleration the rocket needed. c) For how long a time did the rocket need to burn in order to reach 600 m/s? d) What force did the engine need to produce to achieve this acceleration? |
In rocket problem one, the rocket's fuel was regarded as negligible in mass. The following problem will explore the mechanics of the rocket's motion without this assumption. A simple system that works like a rocket is a person sitting in a canoe without any paddles, but with some baseballs. They can use the baseballs instead of paddles to propel themselves. By throwing the baseball in one direction, the canoe will move in the other in accordance with conservation of momentum. A rocket achieves this same effect by expelling gasses at large velocities. The exhaust gas plays the role that the balls do for the canoe, and the combustion of the fuel plays the role of the person throwing the balls.
a) If the canoe contains 100 baseballs, estimate the mass of the person, the canoe, and the baseballs. Also estimate the speed with which a baseball can be thrown, and use this to calculate the speed with which the canoe moves after the first baseball is thrown.
b) If the person continues throwing balls at intervals of ![]() t,
then write an expression that relates the change in velocity
t,
then write an expression that relates the change in velocity
(![]() v) per ball
to the change in the canoe's mass (
v) per ball
to the change in the canoe's mass (![]() m)
per ball.
m)
per ball.
c) In most rockets, the exhaust stream is essentially continuous rather
than discrete balls spaced widely in time. To accommodate this, make the
expression derived in part b into a continuum equation by changing the
![]() 's to differentials
(dt, dm, and dv).
's to differentials
(dt, dm, and dv).
Again consider the rocket needed to examine the ozone layer. This time, do not consider the fuel to be massless.
a) The combustion of 1 kg of kerosene with 3.4 kg of oxygen releases 4.2 x 107 J of energy. If all of this goes into propelling the exhaust gas out of the rocket, what will the exhaust velocity be in the rest frame of the rocket?
b) If the engine thrust is to be the same as it was in rocket problem #1, at what rate must the rocket burn fuel? Was the negligible fuel mass approximation reasonable?
c) Use the expression derived in rocket problem #2 and the effect of
gravity to write an equation for the acceleration of the rocket. Integrate
this to find the velocity and height as functions of time. (Useful equation: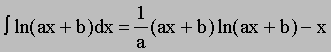 )
)
d) If the rocket is to have the same maximum velocity and reach the same height as the rocket in problem #1, at what rate, and for how long, should the rocket burn its fuel? (Note: Although part c provides two equations and two unknowns, the equations are transcendental. A solution may still be obtained by graphing the two equations and finding their intercept, or by intelligent trial and error using a calculator)
These problems written and collected by K. Vick, E. Redish, and P. Cooney. These problems may be freely used in classrooms. They may be copied and cited in published work if the Activity-Based Physics (ABP) Alternative Homework Assignments (AHAs) Problem site is mentioned and the URL given.
 |
Work supported in part by NSF grant DUE-9455561 |
To contribute problems to this site, send them to redish@quark.umd.edu.
 |
Go back to the AHA page |
Maintained by
University of Maryland PERG
Comments and questions may be directed to
E. F. Redish
Last modified June 25, 2002