
Teaching Physics with the Physics Suite
Edward F. Redish
Home | Action Research Kit| Sample Problems | Resources | Product Information
Problems Sorted by Type | Problems Sorted by Subject | Problems Sorted by Chapter in UP
 |
Teaching Physics with the Physics Suite Edward F. Redish Home | Action Research Kit| Sample Problems | Resources | Product Information |
Problems Sorted by Type | Problems Sorted by Subject | Problems Sorted by Chapter in UP |
A nerve cell or neuron communicates with other nerve cells through a long "process" (this neuroscience technical term to mean something extended out of a neuron) or cable called an axon. This axon is a long thin tube that is electrically active. A drawing of two neurons connected by one of their axons is shown in the figure below. (From B. Alberts et al., Molecular Biology of the Cell, Fourth Edition: Garland Science 2002, p. 1228.)

The function of these axons is to carry electrical signals from one cell to another. This signaling is responsible for carrying data in to the brain from the sensors (eyes, ears, skin) and for carrying signals to muscles to create motion. It is also the critical element in brain functioning of perception and thinking.
The cell membrane of the axon maintains a potential difference of about 70 mV from the inside to the outside of the membrane. It therefore acts as a capacitor. (See the problem Capacitance in Nerve Cells for a discussion of the parameters.)
| Our model of the nerve axon is basically a parallel plate capacitor
"rolled up" into a long cylinder. Its stationary state
has excess negative charge along the interior and excess positive
charge along the exterior, maintaining the potential difference across
the membrane.
When the cell "fires" creating an "action potential" -- a signal that travels down the axon,but that signal is not a current sent down the length of the axon. Rather, what happens in that a small bit of the axon (a small circle along the length) discharges -- like shorting out a capacitor. Charges run radially to create a "blip" in the potential difference along the length. This variation in the potential then runs along the length to carry the signal. As a result, the signal is transverse -- the motion of the charges producing the signal are primarily radial -- perpendicular to the length of the axon and the direction of propagation of the signal. This is similar to what we have seen with a transverse wave on a long elastic string. The motion of the matter of the bits of the string are perpendicular to the length of the spring and the direction of propagation of the signal. |
|
The potential across a membrane as a function of the distance along the axon looks something like shown in the figure below.

In the first image the cell is resting. All along the axon the potential difference across the membrane is -70 mV. In the middle figure a piece of the membrane has discharged (and overshot) producing a pulse in the potential as a function of position along the axon. In the right hand figure, the pulse has moved down the membrane.
Of course the "transverse wave on an elastic spring" picture is only a metaphor. The actual mechanism by which the pulse is generated has to do with ions being pumped across the membrane and the new potential gradient that results passes the potential along analogous to the forces moving the beads in the bead & massless spring model.
In this problem we will use a simplified model to get an idea of what charges are responsible for this pattern and to what extent currents of charge move down the axon. (This is important in understand what is detected when the magnetic field of the brain is measured to study brain processes as in a magneto-encepholograph. Electric currents produce magnetic fields so if there is no current -- or only radial current -- the MEG will not detect action potentials.)
In order to simplify our analysis, let's first ignore the "overshoot" as the potential returns to its stationary value. This potential pattern is shown in model I at the left below. And second, lets look for the extra charges that produce the spike, not the ones responsible for the original potential shift. The resulting potential pattern, ignoring the offset, is shown in model II at the right below.

Now in this simplified model II (the one at the right), we have potentials that change linearly only. We know that we can model a system that produces a linearly changing potential as one with a constant E field (since E = -dV/dx). A simple system that gives a constant field and a linearly changing potential are parallel plates. So we might consider a model, at least temporarily, that has a potential graph (along the dotted line) that looks like the graph above on the right: three parallel plates as shown in the figure below.
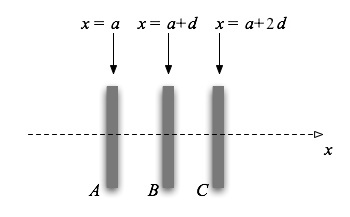
(This doesn't actually look like our axon, which are rings perpendicular to the length of the axon, not plates. But the math in the 1D along the dotted line is the same, so the result is actually quite good.)
What are the signs of the charges that you have to put on plates A, B, and C to get a potential that looks like model II? Never mind about the absolute magnitude of the charges, but tell what sign you have to have on each plate, how they have to compare two each other (equal? twice as big? 10 times as big) and whether the total charge on the plates is positive, negative, or zero. Explain how you got your answer.
This pattern of charge is the pattern that will actually move down the axon, so you can see whether the motion of the pulse is associated with a flow down the axon of positive charge, negative charge, or a net current of 0.
Page last modified March 29, 2012: O58