
Teaching Physics with the Physics Suite
Edward F. Redish
Problems Sorted by Type | Problems Sorted by Subject | Problems Sorted by Chapter in UP
 |
Teaching Physics with the Physics Suite Edward F. Redish |
Problems Sorted by Type | Problems Sorted by Subject | Problems Sorted by Chapter in UP |
| The picture at the right shows the shape of a pulse on a stretched spring at the time t = 0.
The displacement of the spring from its equilibrium position at that
time is given by:
|
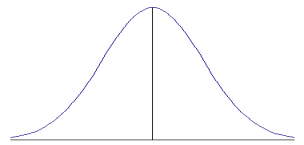 |
(a) Write an equation for the displacement of any portion of the spring at any time, y[x,t]. Specify the height and position of the peak in terms of the symbols given.
(b) Take the velocity to be v0 = 50 cm/s. Use a spreadsheet to calculate the function F[x] for x = - 5 cm to x = +5 cm for A = 2 mm and b = 0.5 cm in x steps of 0.1 cm. Plot a graph showing the shape of the spring at t = 0 and at two later times, t = 0.025 s and 0.05 s. In your writeup include a print out of the tables in your spreadsheet and the three graphs.
Page last modified Febrruary 13, 2011: O56