
Teaching Physics with the Physics Suite
Edward F. Redish
Home | Action Research Kit| Sample Problems | Resources | Product Information
Problems Sorted by Type | Problems Sorted by Subject | Problems Sorted by Chapter in UP
 |
Teaching Physics with the Physics Suite Edward F. Redish Home | Action Research Kit| Sample Problems | Resources | Product Information |
Problems Sorted by Type | Problems Sorted by Subject | Problems Sorted by Chapter in UP |
A. In chemistry, one often uses a unit of charge known as the Faraday, which has the magnitude of the charge of one (gram) mole of electrons. Since the Coulomb has come to be the international standard of unit of charge, the Faraday is taken to have the unit "C/mole" or Coulombs/mole. How many Coulombs/mole is there in a Faraday?
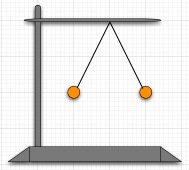
B. In lab, suppose that we take two small aluminum spheres of 1 gram each and hand them from a common support point by 23 cm long non-conducting threads. While they are touching, we use an electrophorus to put some negative charge on the two spheres. Suppose that the two spheres share the charge equally. When the electrophorus is removed, the spheres repel and settle down to hang as shown in the figure at the right.
|
|
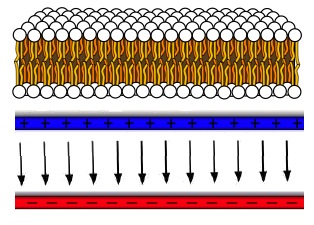
C. An important feature of cellular membranes is that there is an electrical potential difference across them. A typical membrane in an animal cell maintains a potential difference of 70 mV across the membrane. Many membranes are made up of pairs of lipid molecules lined up as shown in the top figure at the right, with their hydophilic ends (small spheres) on the outside and their hydrophobic ends (tails) on the inside. Let's make a simple model of the charge distribution on the membrane that leads to the indicated potential difference. We'll approximate it as two parallel flat sheets of uniform charge with a constant field between them. The thickness of the membrane is about 5 nm. |
 |
1. Let's first ignore the fact that the space between the plates is filled with lipid molecules, and treat it as if there were a vacuum between the plates. Find the electric field between the plates and the charge density on each plate.
2. The diameter of the heads of the lipid molecules are about 0.7 nm and they are closely packed. Any extra charges on the top or the bottom of the membrane have to come in units of the charge on the electron. Estimate the fraction of lipid molecules that have an extra charge.
3. The membrane is not empty, but filled with lipids. This means the space between the plates have a dielectric constant that reduces the field produced by a given charge density. The dielectric constant of the interior of the membrane is about κ ~ 2. How does this change the result you found for part C.2?
Page last modified April 19, 2011: E65