
Teaching Physics with the Physics Suite
Home | Action Research Kit| Sample Problems | Resources | Product Information
Problems Sorted by Type | Problems Sorted by Subject | Problems Sorted by Chapter in UP
 |
Teaching Physics with the Physics Suite
Home | Action Research Kit| Sample Problems | Resources | Product Information |
Problems Sorted by Type | Problems Sorted by Subject | Problems Sorted by Chapter in UP |
In the previous problem, we demonstrate that the force of air resistance on a sphere of radius R can plausibly be argued to have the form
where the v with an arrow is the vector velocity and the v without is its magnitude (the speed). The density of the air, r, is about 1 kg/m3 --- 1/1000 that of water. The parameter C is a dimensionless constant.
If we drop a steel ball and a styrofoam ball from a height of s, the steel ball reaches the ground when the styrofoam ball is still a bit above the ground -- call the distance h. Estimate the air resistance coefficient C as follows:
(b) Since the steel and styrofoam were not very different, use vav, the average velocity of the steel ball during its fall to calculate an average air resistance force, Fav = -b vav2, acting on the styrofoam sphere during its fall. Express this force in terms of b, m (the mass of the styrofoam sphere), g, s, and h.
(c) The average velocity of the steel ball is vav,steel = s/t. The average velocity of the styrofoam sphere was vav,sty = (s-h)/t. Assume this difference is caused by the average air resistance force acting over the time t with our basic Newton's law formula:
Use this to show that
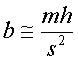
(d) A styrofoam ball of radius R = 5 cm and mass m = 50 gm, is dropped with a steel ball from a height of s = 2 m. When the steel ball hits, the styrofoam is about h = 10 cm above the ground. Calculate b (for the styrofoam sphere) and C (for any sphere).
Not finding what you wanted? Check the Site Map for more information.
Page last modified October 15, 2002: D29