The bouncing ball
an MBL demonstration of the period doubling approach to chaos

Lei Bao
Physics Education Research Group
University of Maryland 

* sponsored in part by NSF grants RED-9355849 and DUE-9455561

Motivations

• Chaos is a new and interesting subject.
• Many students in our class show strong interests in this topic and want to know more.
• The concepts in chaos can also help the understanding of other topics in physics.

Context of the experiment

• We proposed and developed a lab as a possibility for students

• The experiment addresses the transition from the single period motion to multiperiod motion in the approach to chaos

The advantages of the bouncing ball experiment

We try to construct a simple experiment that can easily work in a hands-on lab class.

The experiment of a ball bouncing on an oscillating platform is a very appropriate one.

• The physics is obvious and simple enough to be accepted by students.

• The experiment is easy to perform and shows clear period doubling process all the way to chaos.

Previous research done by others

The bouncing ball experiment is famous and well studied. Many researchers have done excellent jobs on this topic.

P. J. Holmes

Zbigniew J. Kowalik et al

N. B. Tufillaro et al

The bouncing ball laboratory

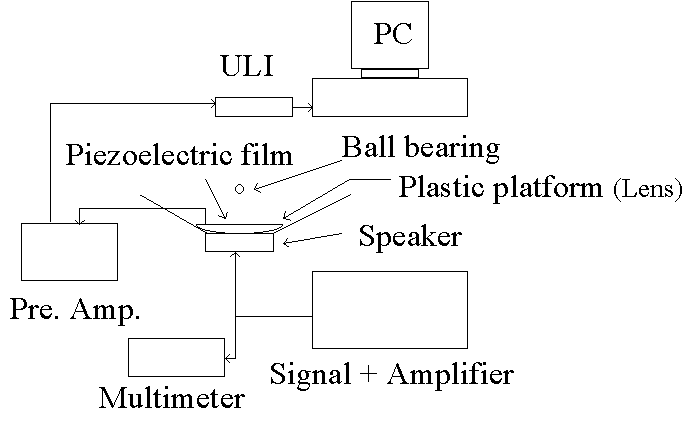
In order to implement the bouncing ball experiment as a lab, we incorporated some new methods into the traditional experiment.

• We use computer with ULI to collect and display the data.

• An analysis tool is also developed with Excel and Visual Basic to help the students analyze the data.

Experiment setup

Interfacing with ULI

• Software: Data Logger

• Probe: electric voltage probe

• Hardware and software configurations

pre amplifier: 300~10khz ( to avoid background noise)

data collection rate: 9000 pt/s for a driving frequency of 80 Hz

The major activities in the experiment

The two activities that we are looking for in the lab are to

• analyze some simple trajectories of typical orbits

• study the period doubling process and construct the bifurcation diagram

Typical trajectories of simple orbits

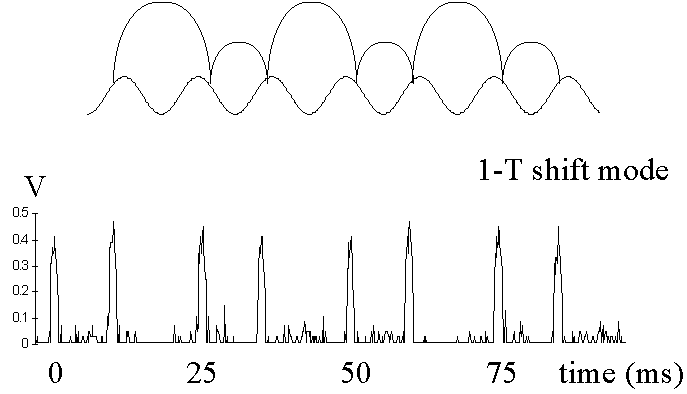
Typical 1-T orbit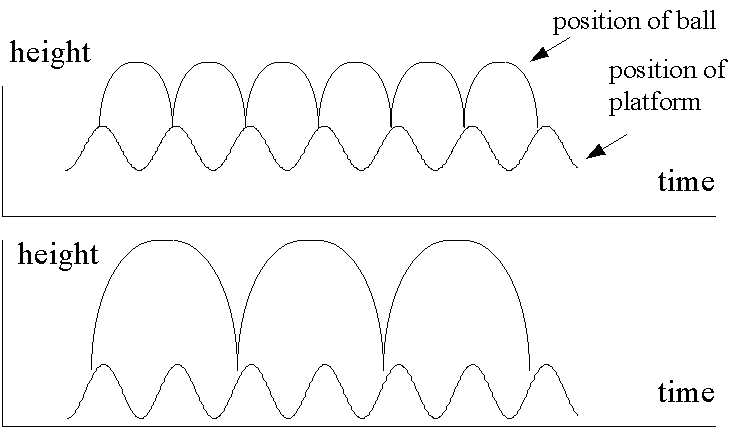

Typical 2-T orbit

Relation between the period and the amplitude of the pulse

The relation between the period for stable even mode orbits and the amplitude of the pulse generated by the collision is:

Vpulse µ F µ Dp = mgT The pulse generated by the piezoelectric film is proportional to the force acting on the film The velocity of the ball right before the next collision happens is: v = 1/2gT => Dp = mgT

Consider the 1-T and 2-T orbits. The ball in a 2-T orbit stays in the air twice longer than in a 1-T orbit, therefore the pulse generated in 2-T orbit should be twice as large.

The signal output shown on the computer

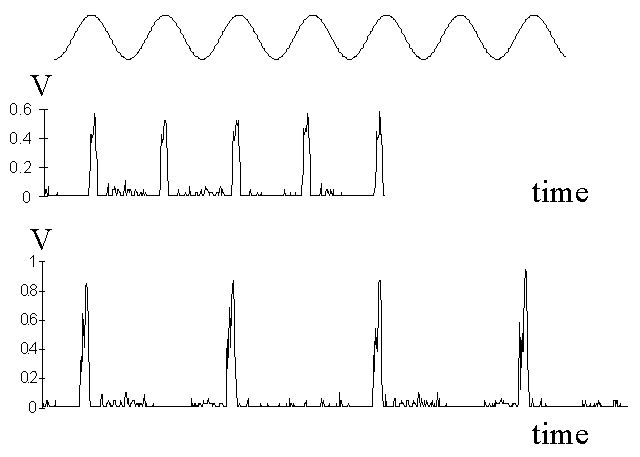
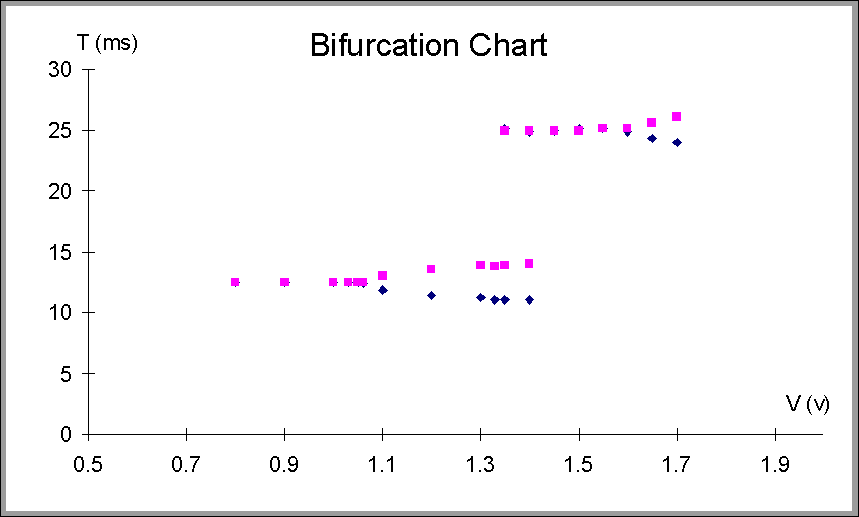
Period doubling

Shift mode of the 2-T period

Bifurcation diagram

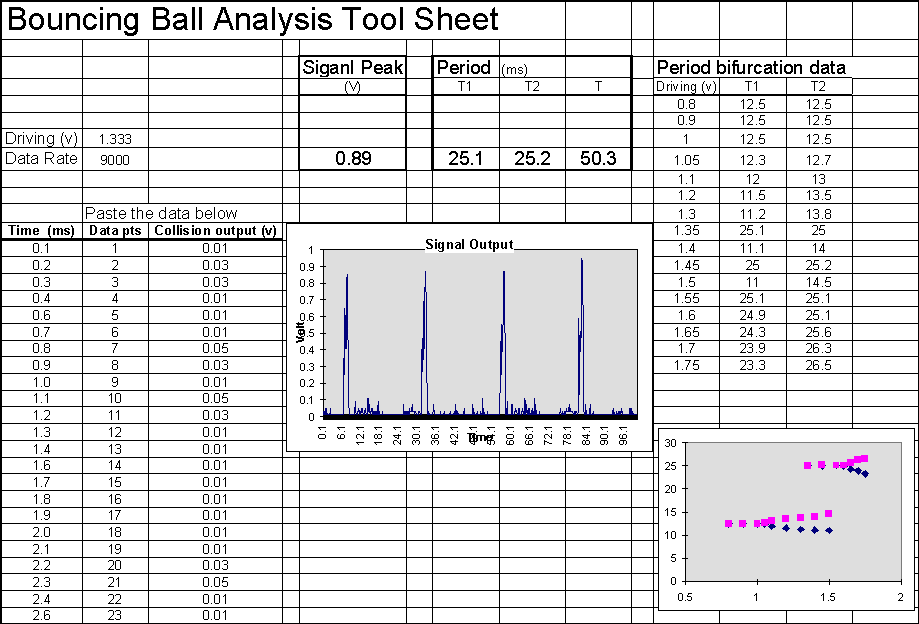
Iterative process of research, instruction, and curriculum development

• conducting investigation of student understanding

• applying results to the development of instructional strategies

• designing, testing, modifying and revising curriculum in a continuous cycle