Millikan Award Lecture (1998):
Building a Science of Teaching Physics
Building a Science of Teaching Physics
Edward F. Redish
University of Maryland, College Park
University of Maryland, College Park
Published July, 1999, in The American Journal of Physics.
 This work was supported in part by NSF grants DUE
945 5561 and DUE 965 2877.
This work was supported in part by NSF grants DUE
945 5561 and DUE 965 2877.
Abstract
Individual teachers of college level physics sometimes develop deep insights into how their students learn and what elements of classroom instruction are valuable in facilitating the learning process. Yet these insights rarely persist beyond the individual instructor. Educational methods seem to cycle from one fad to another, rarely cumulating increasingly powerful knowledge in the way scientists expect understanding to grow. In this paper I explore the character of our understanding of the physical world and of teaching about it. The critical factor is using "the culture of science" ó the set of processes that allow us to build a community consensus knowledge base. Elements of the beginning of a base for our educational knowledge are discussed and examples given from discipline-based physics education research.
I. Introduction: Why does science cumulate knowledge while education seems not to?
In 1903, Robert Millikan published the first volume of a two volume reform curriculum in introductory physics. In the preface to this volume he makes the following statement: [1]
The most serious criticism which can be urged against modern laboratory work in Physics is that it often degenerates into a servile following of directions, and thus loses all save a purely manipulative value. Important as is dexterity in the handling and adjustment of apparatus, it can not be too strongly emphasized that it is grasp of principles, not skill in manipulation which should be the primary object of General Physics courses.
He goes on to discuss the character of his new course in which lectures and laboratories are closely entwined. Priscilla Laws has already discussed Millikanís laboratory-based course in some detail in her 1996 Millikan Lecture [2] so I will not go into detail here. Fourteen years later, in 1917, Millikan published a small volume entitled The Electron.[3] This volume includes a discussion of Millikanís determination that it makes sense to talk about the electron as having a fixed charge:
Here, then, is direct, unimpeachable proof that the electron is not a ëstatistical mean,í but that rather the electrical charges found on ions all have either exactly the same value or else small exact multiples of that value.
The implications of Millikanís comments on the nature of the electron have been included in nearly every introductory physics text since soon after the results were published. Indeed, the issue as to whether the electronís charge may assume continuous or discrete values is almost never considered as a possibility, his result is so well ingrained. Yet few people today know of Millikanís reform curriculum and his description of the issues it is meant to deal with sounds both modern and pertinent. The type of curriculum he developed for college physics has vanished and reappeared only to vanish again with maddening regularity during the nearly 100 years since he proposed it. Melba Phillips said it best when she said: "The trouble with problems in physics education is they donít stay solved."[4]
What is it that allows us to build our knowledge of physics in a cumulative way while in physics education we seem to be doomed to everlasting cycles of pushing the Sisyphian rock up the hill only to have it roll down again? Why do we never seem to be able to share and pass down to succeeding generations what we learn about physics education? Is there anything we can do to change this unhappy situation or is it part of the fundamental character of education and of human beings?
In order to understand the elements needed for us to cumulate knowledge about physics education, we need to consider what it is about physics (and about science in general) that leads to successful accumulation of knowledge in those fields. In this paper I begin with a discussion of the nature of scientific knowledge and consider those elements that lead to accumulation of knowledge. I then discuss the embedding environment of physics education ó the general principles of learning theory that have been developed by cognitive scientists and education theorists. Next, I present examples of what sort of knowledge has been obtained from physics education research. The paper concludes with a discussion of how a science-like physics education research enterprise fits into physics as a whole and the value it can have for the community of physicists. Throughout, I explicitly discuss those elements which are controversial, confusing, or commonly misconstrued.
II. The process of science creates an accurate (but approximate) community map of the physical world.
We often say that the goal of science is to discover the laws of nature. This is not quite precise enough for our purposes. Itís better to say that we are trying to create the best way of thinking about the world that we can. This places the knowledge firmly where it really resides ó in the head of the scientist.
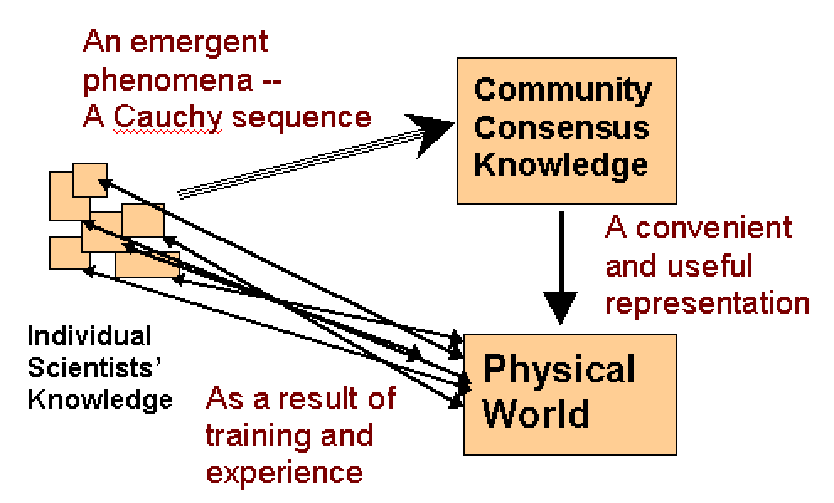
A good metaphor for the process of science is the building of a map. A map of the world should not be mistaken for the world,[5] but it can nonetheless be of great value in getting around. What is perhaps most important about the scientific map of the world is that it is more than just the collection of the maps of individual scientists. The culture of science includes the continual interaction, exchange, evaluation, and criticism we make of each otherís views. This produces a kind of emergent phenomenon I refer to as a community consensus knowledge base or more briefly, a community map. I visualize this as an idealized atlas of science. Just as an atlas contains many individual charts, the atlas of science contains many distinct coherent but incomplete areas of knowledge. These areas are supposed to agree where they overlap, but it is not clear that the entire universe can be encompassed in a single map.[6] No single individual, no matter how brilliant, contains a map identical to this community consensus map.