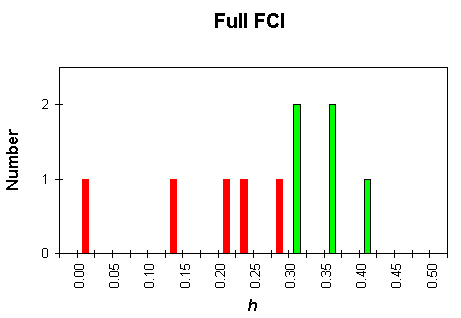
Fig. 4: Figure of merit histogram. h = fraction of possible gain obtained on the full FCI, for tutorial (gray bars) and non-tutorial (solid bars) lecture classes.
The results are displayed as a figure of merit (h) histogram in Fig. 4. The classes taught without tutorials are shown as red bars, while those taught with tutorials are shown as green bars.

<h> = 0.18 (5 classes, with recitations)
<h> = 0.35 (5 classes, with tutorials)
Note that this average is taken as equally weighted over lecture class, not by student. Every tutorial class had a larger h than every non-tutorial class[20] Even the tutorial results are somewhat disappointing, achieving only about 1/3 of the possible gain. Both results, however, are consistent with Hake's survey (ref. 18). The non-tutorial scores are consistent with those of other traditional classes, and the tutorial results are about halfway between those of traditional and highly interactive non-traditional classes.Assuming that all 10 classes are drawn from the same population, the probability that the shift of the means is random is less than 2% using a 2-tailed t-test with pooled variance.[21] If class E is excluded as an outlier, the probability that the shift in the means is random is less than 1%.
The same amount of instruction was offered students in both environments (3 hours of lecture and 1 hour of small class section). The primary difference in the tutorial and traditional classes is that the tutorial classes spend one hour per week on explicit concept building in a small-class group-learning-style environment, while the traditional classes spend one problem solving hour per week in a small-class lecture-style environment.
In class A3, the tutorial system was in place, and one hour of tutorial was given as described in section III. The professor reduced the lecture time on the topic to a single hour, which was more typical of a traditional lecture and had little student interaction. In both classes, the questions were given as part of an examination and, contrary to Thornton and Sokoloff, were not previously given to the students as homework. The results for the error rates are given in Table 2 and shown in Fig. 5.
| Instruction without MBL | Q1 | Q2 | Q3 | Q4 | Q5 |
|---|---|---|---|---|---|
| U. Md.(a) | 29 | 7 | 62 | 37 | 14 |
| Tufts(b) | 18 | 7 | 41 | 18.5 | 17 |
| 6 school av.(c) | 41 | 17 | 63 | 37 | 6 |
| Instruction with MBL | Q1 | Q2 | Q3 | Q4 | Q5 |
| U. Md.(d) | 6 | 2 | 30 | 19 | 5 |
| Tufts(b) | 2 | 7 | 5 | 3 | |
| 6 school av.(c) | 11.5 | 2 | 13 | 11 | 7 |
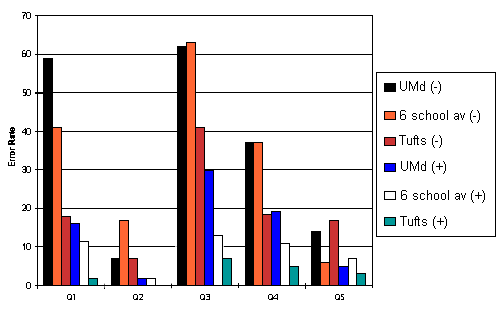
Fig. 5: Error rate on T&S velocity questions (VQ).
These results are consistent with those given by Thornton and Sokoloff. The fact that these results have been obtained with both the lecturer and the time of instruction controlled strongly supports the results in Thornton and Sokoloff and answers our question Q1 in favor of the MBL. The MBL activities play a significant role in the improvement of student understanding of the concept of velocity. It is not simply the extra time that is responsible. It also suggests as a partial answer to our question Q3: simply enhancing lectures is not effective in producing an improvement in the learning of the velocity concept for a significant number of students.
| Question | 2 | 11 | 13 | 14 | hN3 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Class | Pre | Post | h | Pre | Post | h | Pre | Post | h | Pre | Post | h | |
| A2 | 26% | 66% | 0.54 | 53% | 82% | 0.61 | 37% | 34% | -0.04 | 63% | 82% | 0.50 | 0.40 |
| A3 | 39% | 89% | 0.82 | 44% | 87% | 0.77 | 14% | 52% | 0.44 | 73% | 88% | 0.57 | 0.65 |
| B1 | 22% | 67% | 0.57 | 41% | 78% | 0.62 | 18% | 52% | 0.41 | 63% | 74% | 0.30 | 0.48 |
| B2 | 37% | 53% | 0.25 | 47% | 68% | 0.40 | 26% | 58% | 0.43 | 68% | 68% | 0.00 | 0.27 |
| C1 | 23% | 32% | 0.12 | 31% | 46% | 0.21 | 21% | 43% | 0.28 | 54% | 66% | 0.25 | 0.22 |
| C2 | 39% | 44% | 0.09 | 39% | 39% | 0.00 | 28% | 28% | 0.00 | 50% | 67% | 0.33 | 0.11 |
| D1 | 38% | 91% | 0.86 | 45% | 90% | 0.82 | 29% | 70% | 0.57 | 59% | 93% | 0.82 | 0.77 |
| D2 | 35% | 66% | 0.47 | 40% | 73% | 0.55 | 21% | 46% | 0.32 | 58% | 90% | 0.75 | 0.52 |
| E | 19% | 45% | 0.32 | 52% | 60% | 0.15 | 24% | 40% | 0.22 | 60% | 64% | 0.12 | 0.20 |
| F | 26% | 76% | 0.68 | 46% | 85% | 0.73 | 24% | 56% | 0.43 | 60% | 89% | 0.73 | 0.64 |

Fig. 6: Histogram of average figures of merit for the Newton 3 FCI cluster. Solid bars are for classes not using the MBL tutorial, gray bars for those using the MBL tutorial.
<hN3> = 0.28 (6 classes, without Newton 3 MBL tutorial)
<hN3> = 0.64 (4 classes, with Newton 3 MBL tutorial)
In the first semester in which tutorials were tested, there was no tutorial specifically oriented towards Newton 3. Our tutorial was written for the subsequent semester. As a result, the first Maryland tutorial class, A2, used tutorials but not a Newton 3 MBL tutorial. This, therefore, gives us a control for individual lecturer as well as for the presence of tutorials. (No special effort was devoted to Newton 3 in lecture in either case.) The result is:
<hN3> = 0.40 (A2: without Newton 3 MBL tutorial)
<hN3> = 0.65 (A3: with Newton 3 MBL tutorial)
Students from both classes struggled with this question. Table 4 shows a breakdown of student responses.
| % correct (a) | % apparently correct, but ending at v=0 (b) | % other incorrect responses | |
|---|---|---|---|
| Recitation (N=50) | 12 | 10 | 78 |
| Tutorial (N=82) | 22 | 21 | 57 |
Only a small fraction of the students in either class were able to draw a graph that reflected the critical features, but the tutorial students did better than the students in the recitations. After traditional instruction, 12% of the students drew a correct graph. After MBL tutorials, 22% of the students drew a correct graph.
Analysis of the incorrect graphs along with the accompanying explanations revealed some of the students' difficulties. Many students showed in a variety of ways that they had the well-documented confusion between position and velocity. Some drew graphs that at first glance appear correct: the graph increased linearly for the first 3 seconds and then decreased linearly after. However the graph ended at v=0, and some of these students indicated that this coincided with the cart returning to its starting location. Many drew graphs that had incorrect combinations of linear segments, including discontinuities in velocity. Others drew dramatically curved features in their velocity-time graphs. Most of these graphs indicated severe conceptual difficulties even if interpreted as a position vs. time graph. It is worth noting that it is clear from many of their explanations that the students intended to draw a velocity vs. time graph.
Both the percentage of correctly drawn graphs and the nature of the incorrect graphs confirm that while student difficulties understanding kinematics is pervasive even after instruction, the modified instruction described earlier in this paper appears to be helping address these difficulties. Although the VQ were not given in these classes, approximately 70% of the students in the comparable tutorial class A3 answered all of the multiple choice questions correctly, while only about 40% of those in the recitation class A1 answered them all correctly. The relative results on the long-problem are qualitatively consistent with the results of the VQ, but the absolute number of students getting correct answers on the long-problem was substantially lower (22% of the tutorial students correct vs. 12% of recitation students correct). Since no classes were evaluated with both the VQ and the long problem, we cannot completely answer Question Q2, but our indications are that the VQ may not suffice. Our results suggest that answering multiple-choice questions correctly is not sufficient to guarantee a robust and fully functional understanding of the relevant concepts for a significant number of students.
The breakdown of student responses to this part of the question is shown in Table 5.
| % correct | % used the same symbol but did not compare forces | % stated third law force pair have different magnitudes | % no identification of contact forces | % other incorrect response | |
|---|---|---|---|---|---|
| Recitation (N=50) | 42 | 6 | 22 | 14 | 16 |
| Tutorial (N=82) | 55 | 0 | 40 | 1 | 4 |
In the tutorial classes, 55% of the students correctly identified and compared the third law force pair. In the non-tutorial class 42% identified and correctly compared these forces.[23] (This result favoring the tutorial class is particularly notable since their pre-test N3 FCI scores were lower than the recitation classes's score, 38% correct to 44% correct.) Many students identified that the two carts were exerting forces on one another, but stated explicitly that the two forces were not of equal magnitude. In addition, there were also many students who did not even recognize that the two carts exert forces on each other. This was particularly common in the non-tutorial class.
These results should be compared with the results on the post-test N3 FCI questions for the same two classes, 69% and 62% respectively. The discrepancy between the multiple-choice and long-answer problems (in this case both questions were done by both groups) also suggests that the answer to question Q2 might be: the short answer results provide an indication, but overestimate the students' knowledge.
The velocity issue was probed by using the multiple choice velocity graph-matching questions given in ref. 3 in two classes taught by the same professor. In one class, the material was taught in lecture with additional lectures given on the subject and the professor doing his best to "teach to the test" without actually doing the test questions in class. In a second class, the professor ignored the test but a single hour of tutorial based on Tools for Scientific Thinking was given. In the non-tutorial class the results were very close to the six school average of lecture classes reported in ref. 5. In the tutorial class, the error rates fell by more than a factor of 2 for all questions. Although this result is not as dramatic as those produced by Thornton and Sokoloff after four additional hours of MBL laboratory, the results are still impressive, especially since we controlled for both the instructor and the time of instruction.
In our second experiment, we constructed a tutorial using MBL on the subject of Newton's third law. In this case, we used the four relevant questions from the FCI in pre- and post-testing as an evaluation tool. Of the ten classes tested, the tutorial was given in 4 lecture classes with three different professors, and it was not given in 6 lecture classes with three different professors. One of the professors taught a class in each group giving us a specific control for instructor. Both the absolute gains and the final total scores favor the tutorial classes with every tutorial class scoring a higher fraction of the possible gain (hN3) than every non-tutorial class. The professor who did both a recitation and tutorial section, found his class's value of hN3 increase by 60% when he used the tutorial.
We therefore conclude that our answer to question Q1 is: targeted MBL tutorials can be effective in helping students build conceptual understanding, but do not provide a complete solution to the problem of building a robust and functional knowledge for many students.
A long problem requiring the application of the velocity concept, the building of a velocity graph, and the application of Newton's third law in a complex situation was also given to one tutorial and one recitation class. The tutorial students performed better than the recitation students. In the N3 case where both short and long answer data were available for the same class, the long answer results favored the tutorial students slightly more strongly than the multiple choice questions. But in all cases, the number of students able to produce the correct concept in a complex situation was significantly less than suggested by the multiple choice questions. This indicates that the answer to question Q2 is: multiple choice tests are qualitatively indicative of the direction of change, but cannot be used to determine the extent of robust and functional knowledge developed by the class.
In this experiment we did not test for "side effects",[24a] Since the MBL activities were added at the expense of problem-solving recitations we should also test whether there was a deterioration in problem-solving for students who did tutorials instead of recitations. We do not expect a significant effect as our personal anecdotal evidence suggests that recitations are effective for only a small fraction of students. This should, however, be tested in more detailed studies. There are strong indications from earlier work[24] that successful problem solving at the introductory level is often not associated with a growth in conceptual understanding. It may be that only a small fraction of students can successfully learn physics in the order: algorithms first, understanding second; and that it would be more effective for most students to reverse the order.
Thornton and Sokoloff conjectured that the MBL activities they had designed were unusually effective for five reasons:
These conjectures are consistent with modern theories of learning,[25] including those built on the work of Piaget and Vygotsky, and on our current understanding of the structure of short and long-term memory buffers.[26] To this list we add a sixth conjecture: 6. Students are actively engaged in exploring and constructing their own understanding.
The Thornton-Sokoloff conjectures appear to be confirmed by a variety of anecdotes describing the success of the substitution of active-engagement MBL activities for traditional labs, and by the failure of the same equipment when used as traditional labs without the engagement/discovery component.[27] These have not, unfortunately, been documented in the literature. It would be useful to have additional detailed experiments comparing different methods in order to build an understanding of exactly what components of MBL activities are proving effective.
Since we relied on all of the Thornton and Sokoloff conjectures (and one of our own) in building our units, we are unable to distinguish which of the elements are critical.[28] Note that the impact of all of the six conjectures could well be achieved without the use of MBL equipment. It would be most interesting to carry out additional large scale studies of the effectiveness of active engagement activities that do not include MBL on the learning of specific concepts.
[21] Howell, David C., Statistical Methods for Psychology, 3rd Ed. (Duxbury Press, Belmont, California 1992) pp. 181-185.
[22] A graph reversed with respect to the horizontal axis would also be considered correct.
[23] A few students in the non-tutorial class used the same symbol for these two forces, but did not state whether the forces were equal, so it was impossible to determine if they were identifying these two forces as having equal magnitudes. Note that many students used the same symbol to represent forces which clearly had different magnitudes.
[24] Frederick Reif, "Millikan Lecture 1994: Understanding and teaching important scientific thought processes" Am. J. Phys. 63 (1995) 17-32.
[24a] Evidence from the University of Washington group suggests that replacing a problem solving lecture with tutorials does not adversely affect students' ability to solve quantitative problems. Personal communication, Lillian C. McDermott.
[24b]Note that when a student is learning what a graph means, constructing it by hand the first few times may very well be "necessary" drudgery. However, when one is focusing on a connection between a physical phenomenon and a graph, a long time delay between seeing the phenomenon and seeing the graph may well produce a "cognitive disconnect" which prevents them from building the understandings they need.
[25] See references in ref. 15.
[26] Daniel L. Schacter, "Memory", in Foundations of Cognitive Science, M. I. Posner, ed. (MIT Press, Cambridge MA, 1989) 683-725.
[27] Ronald K. Thornton, private communication, January 1994.
[28] From our personal teaching experience, we expect that number 6, active engagement, is the most significant.
©1997, American Association of Physics Teachers.
Click here to return to part 2.
| University of Maryland | Physics Department | PERG UMD |
|---|---|---|
 |  |  |