General
- Estimate the total number of hairs on your head.
- Estimate the number of square inches of pizza consumed by all the students
at the University of Maryland during one semester.
- When it rains, water would accumulate on the roofs of flat-topped buildings
if there were no drains. A heavy rain may deposit water to a depth of an
inch or more. Given that water has a mass of about 1 gm/cm 3 ,
estimate the total force the roof of the physics lecture hall would have
to support if we had an inch of rain and the roof drains were plugged.
- One suggestion for putting satellites into orbit cheaply without using
rockets is to build a tower 300 km high containing an elevator. One would
put the payload in the elevator, lift it to the top, and just step out
into orbit. Ignoring other problems (such as structural strain on the tower),
estimate the weight of such a tower if its base were the size of Washington
DC and it were made of steel. (Steel is about 5 times as dense as water,
which has a density of 1 gm/cm 3 .)
- Estimate the total amount of time 19 year olds in the US spent during
this past semester studying for exams in college. (Not counting finals.)
- The deficit in the Federal Budget this past year was approximately
$100 Billion ($10 11 ).
(a)Assuming this was divided equally to every man, woman, and child
in the country, what is your share of the debt?
(b) Supposing the deficit were paid in $1 bills and they were layed
out on the ground without overlapping. Estimate what fraction of the District
of Columbia could be covered.
(c) Suppose you put these $1 bills in packages of 100 each and gave
them away at the rate of 1 package every 10 seconds. If you start now,
when will you be finished giving them away?
(d) Are any of these calculations relevant for a discussion which is
trying to understand whether the deficit is ridiculously large or appropriate
in scale? Explain your reasoning.
- The Federal Budget Deficit is approximately $100 Billion this year.
Compare this to what we spend on what we eat by estimating the total amount
US consumers spend on food in grocery stores, markets, and restaurants
in one year.
- In the 1989 Loma Prieta earthquake in California, approximately 2 million
books fell off the shelves at the Stanford University library. If you were
the library administrator and wanted to hire enough part-time student labor
to put the books back on the shelves in order in 2 weeks, how many students
would you have to hire? (You may assume that the books just fell off the
shelves and got a bit mixed up but books in different aisles did NOT get
shuffled together.)
- Estimate the total number of sheets of 8.5 x 11 inch paper used by
all the students at the University of Maryland in one semester.
- If the land area of the earth were divided up equally for each person
on the planet, about how much would you get?
- After the gulf war, large areas of desert had to be cleared of mines
using special bulldozers that simply sweep the sand in front of them like
a snowplow, but whose blades are strong enough to withstand the explosion
of a mine. Estimate how long it would take a single bulldozer to clear
a patch of desert that is 10 km square.
- This winter, the East coast has been hit by a number of snow storms.
Estimate the amount of work a person does shoveling the walk after a snow
storm. Among your estimates you may take the following:
- The length of a typical path from a house to the street is 10 meters.
- Assume the snow fell to a depth of 4 inches.
- Assume the snow was only moderately packed so that its density was
equal to 0.2 g/cm 3 -- about one fifth that of water.
In doing this problem, you should estimate any other numbers you need
to one significant figure. Be certain to state what assumptions you are
making and to show clearly the logic of your calculation. (In this problem,
the answer is only worth 2 points. Almost all of the credit is given for
your showing correct reasoning clearly.)
- A floppy disk for a computer stores information by magnetizing small
regions of the disk. For a typical floppy disk, estimate the area of the
disk that corresponds to a single bit of information. (Remember: the storage
capacity of a disk is cited in bytes where 1 byte = 8 bits.)
- Ali El-Ectrical is an Engineering student at your university taking
a "normal" load (for Engineers!) and paying full tuition. Estimate
how much he is paying for each hour of class time he spends with an instructor
over one semester.
- Estimate the number of blades of grass a typical suburban house's lawn
has in the summer.
- How many notes are played on a given radio station in a given year?
- How many pencils would it take to draw a straight line along the entire
Prime Meridian of the earth?
- If all the string was removed from all of the tennis rackets in the
US and layed out end-to-end, how many round trips from Detroit to Orlando
could be made with the string?
- How many drops of waters are there in all of the Great Lakes.
- How many piano tuners are there in New York?
- How many atoms are there in the jurisdiction of the continental US?
- How far can a crow fly without stopping?
- How many golf balls can be fit in a typical suitcase?
- How tall is this building?
- Estimate the number of cars and planes entering the state at any given
time.
- How much air (mass) is there in the room you are in?
- How long does it take a light bulb to turn off?
- ow much energy does it take to split a 2x4?
- How much milk is produced in the US each year?
- If you drop a pumpkin from the top of a ten story building what is
the farthest a single pumpkin seed can land from the point of impact?
- How many flat tires are there in the US at any 1 time?
Mechanics
- Estimate the angular momentum that your body has as a result of the
earth's turning on its axis.
- The mass of the earth is about 6x10 24 kg. Estimate the
kinetic energy it has as a result of its orbiting the sun.
- A professor of physics is going ice skating for the first time. He
has gotten himself into the middle of an ice rink and cannot figure out
how to make the skates work. Every motion he makes simply slips on the
ice and leaves him in the same place he started. He decides that he can
get off the ice by throwing his gloves in the opposite direction.
(a) Suppose he has a mass M and his gloves have a mass m. If he throws
them as hard as he can away from him, and they leave his hand with a velocity
v. Explain whether or not he will move. If he does move, calculate his
velocity, V.
(b) Discuss his motion from the point of view of the forces acting on him.
(c) If the ice rink is 10 m in diameter and the skater starts in the center,
estimate how long it will take him to reach the edge, assuming there is
no friction at all.
- The orbiting Hubble telescope was recently repaired by a crew of astronauts
from the Space Shuttle Endeavor. The Hubble is in a circular orbit 600
km above the surface of the earth. For half of the Hubble's orbital period
it is in sunlight and for half it is in the darkness of the earth's shadow.
As a results of the change in fit of the various parts of the Hubble due
to heating and cooling of the telescope, the astronauts could only work
on certain repairs while the Hubble was in darkness. Estimate how much
time the astronauts had to work on these repairs before having to stop
"for a sun-break".
- According to Newton's law of universal gravitation, the earth's gravity
gets weaker as we go further from the earth. But when we drop a ball near
the top of the lecture hall it doesn't seem to fall any differently than
we drop it near the floor. Let g t stand for the gravitational
acceleration observed at the top of the lecture hall and g b for
it at the bottom. Estimate how much Newton's universal gravitation theory
predicts g t will be less than g b . (Hint: It's
easier if you estimate the fractional change, g b /g t
- 1.)
- Suppose the Army Corps of Engineers decided to put a dam across the
Potomac River in order to provide power for the Washington area. Assume
the dam was built to hold back the water into a lake to a height of 15
m behind the dam. (Ignore the fact that this lake would cover land occupied
by houses and cities.) Estimate the total force the water would exert on
the dam. (Hint: If you have never seen the Potomac and have no idea as
to how wide it is across, make a reasonable guess.)
- A ballistic rocket is shot straight up from Cape Canaveral. Its rockets
fire briefly. After the firing, it has it a velocity of 8 km/sec and a
mass of m. How far up will it go before it begins to fall back to earth?
Calculate your answer to within 10%. Ignore the distance it travels while
its rockets are firing, the resistance of the atmosphere, and the rotation
of the earth. (Hint: If you don't remember the radius of the earth you
can solve for d/R e where d is the distance it reaches measured
from the center of the earth and R e is the radius of the earth.)
- For next year's Physics Open House the Department is planning to set
up a bungee jump from the top of the physics building. Assume that one
end of an elastic band will be firmly attached to the top of the building
and the other to the waist of a courageous participant. The participant
will step off the edge of the building to be slowed and brought back up
by the elastic band before hitting the ground (we hope). Estimate the length
and spring constant of the elastic you would recommend using.
- Estimate the angular momentum an automobile tire has about its axis
of rotation while the car is driving on the interstate.
- In testing a design for a yo-yo, an engineer begins by constructing
a simple prototype -- a string wound about the rim of a wooden disk. She
puts an axle riding on nearly frictionless ball bearings through the axis
of the wooden disk and fixes the ends of the axle. In order to measure
the moment of inertia of the disk, she attaches a weight of mass m to the
string and measures how long it takes to fall a given distance.
(a) Assuming the moment of inertia of the disk is given by I, and the
radius of the disk is R, find the time for the mass to fall a distance
h starting from rest.
(b) She doesn't have a very accurate stopwatch but wants to get a measurement
good to a few percent. She decides a fall time of 2 seconds would work.
How big a mass should she use? Imagine you were setting up this experiment
and make reasonable estimates of the parameters you need.
- According to some recent highly accurate measurements made from satellites,
the continent of North America is drifting at a rate of about 1 cm per
year. Assuming a continent is about 50 km thick, estimate the kinetic energy
the continental US has a a result of this motion.
-
| While on travel this past summer, I passed through Charles
deGaulle airport in Paris, France. The airport has some interesting devices,
including a "people mover" -- a moving strip of rubber like a
horizontal escalator without steps. It became interesting when the mover
entered a plastic tube bent up at an angle to take me to the next terminal.
I managed to get a photograph of it. It is shown in the figure below. If
you were building this people mover for the architect, what material would
you choose for the surface of the moving strip? (Hint: You want to be sure
that people standing on the strip do not tend to slide down it. Figure
out what coefficient of friction you need to keep from sliding down and
then look up coefficients of friction in tables in reference books in the
engineering library to get a material appropriate for the slipperiest shoes.) |
 |
- Estimate the angular momentum of the earth due to its daily rotation about its axis. The average density of the earth is about 5 grams/cm3.
Estimate the angular momentum of the earth due to its daily rotation about its axis. The average density of the earth is about 5 grams/cm3.
Oscillations and Waves
-
| Consider a pendulum of mass m and length L.
(a) Derive the energy conservation equation for the motion of the pendulum.
(Do not use the small amplitude approximation.)
(b) If the pendulum is released from a starting angle of theta 0 ,
what will be the maximum speed it travels at any point on its swing?
(c) When on vacation this summer, I visited a forest which had many waterfalls.
At one of the waterfalls, a long rope hung down from the top of the cliff
near the waterfall and had a seat on the bottom. Adventurous visitors could
hop onto the seat and swing down into the waterfall as shown in the photo
at the right. I estimated that their starting angle was about 20º.
I also timed their swing and discovered it took them 8 seconds to swing
out and back. Estimate the length of the rope and the speed with which
they passed through the waterfall. (The top of the rope is not shown in
the photo.)
|
 |
- You decide to build a pipe organ in your dormitory room using PVC pipe.
Estimate whether you could build an organ that would cover the entire range
of human hearing without bending any pipes.
- In lecture, the oscillations of a mass hanging on a spring was demonstrated.
After a few minutes, the oscillation died down. The mass used had a mass
of M = 50 grams, the spring had a spring constant of k = 5 Newtons/meter
and the spring had a mass of m = 5 grams. Estimate the rise in temperature
of the spring. State clearly all the numbers you are estimating and begin
with a few sentences explaining what physical principles will be relevant
in carrying out your calculation.
Thermodynamics and Kinetic Theory
- The effect of air pressure was demonstrated in 1654 in Magdeburg, Germany
with an impressive experiment. Two hollow metal hemispheres with a flat
metal rim (flange) were placed together and the air removed from the interior
with a primitive vacuum pump. The external pressure of the air pushed them
together. When they tried to pull the hemispheres apart using two rings
welded to the hemispheres, they could not be pulled apart even by a number
of people pulling together. The sphere produced by putting the two hemispheres
together is about the size of a basketball. Estimate the force needed to
pull them apart.
- The density of water is just about 1000 kg/m 3 . The density
of air is just about 1000 times less -- 1 kg/m 3 (actually 1.3
kg/m 3 at sea level.) From your knowledge of the air pressure
at ground level, estimate the height of the atmosphere. As a simplifying
assumption, take the atmosphere to be of uniform density up to some height
after which the density rapidly falls to zero. (In reality, the density
of the atmosphere decreases as we go up.)
- The actual diameter of an atom is about 1 Angstrom (10 -10
m). In order to develop some intuition for the molecular scale of a gas,
assume that you are considering a liter of air (mostly N 2 and
O 2 ) at room temperature and a pressure of 105 Pa.
(a) Calculate the number of molecules in the sample of gas.
(b) Estimate the average spacing between the molecules.
(c) Estimate the average speed of a molecule using the Maxwell-Boltzmann
distribution.
(d) Suppose that the gas were rescaled upwards so that each atom was the
size of a tennis ball (but we don't change the time scale). What would
be the average spacing between molecules and the average speed of the molecules
in miles/hour?
- Converting the kinetic energies we are used to experiencing into thermal
energy typically produces small rises in temperature. This was in part
responsible for the difficulty in discovering the law of conservation of
energy. It also implies that hot objects contain a lot of energy. (This
latter comment is largely responsible for the industrial revolution in
the 19th century.) To get some feel for these numbers, carry out three
estimates:
(a) A steel ball is dropped from a height of three meters onto a concrete
floor. It bounces a large number of times but eventually comes to rest.
Estimate the ball's rise in temperature.
(b) Suppose the steel ball you used in part (a) is at room temperature.
If you converted all its internal energy to kinetic energy, how fast would
it be moving? (Give your answer in units of miles per hour. Also, ignore
the fact that you would have to create momentum.)
(c) Suppose a nickel-iron meteor falls to the earth from deep space. Estimate
how much its temperature would rise on impact.
For each of these problems be sure to state you assumptions clearly
and show your reasoning.
Electricity and Magnetism
- We know that within the limits of measurement, the magnitudes of the
negative charge on the electron and the positive charge on the proton are
equal. Suppose, however, that these magnitudes differed from each other
by as little as 0.0001% (1 part in a million). With what force would two
copper pennies, placed 1.0 m apart, then repel each other? (At 1 m apart,
you may treat the pennies as point charges.)
- Two hard rubber spheres of mass of about 10 g are rubbed vigorously
with fur on a dry day. They are then suspended from a rod with two insulating
strings. They are observed to hang at equilibrium as shown in the figure
on the right, which is drawn approximately to scale. Estimate the amount
of charge that is found on each sphere.
-
| In a tutorial at the University of Maryland, we used a coil
of 10 loops of wire with diameter of the loop about 2 inches to build a
motor with a hand held bar magnet and a 1.5 Volt battery. (See figure.)
This apparatus can also be used to build a generator that will produce
a voltage.
(a) Explain the setup that one would use to do this and explain how
it works.
(b) Estimate the maximum voltage that would be produced if you cranked
the generator by hand.
(Hint: As a comparison for estimating the strength of the bar magnet, the
earth's field at our location is about 0.4 G.)
|
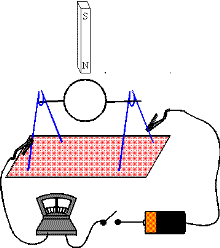 |
- There have been some experiments with DC power transmission. A large
high voltage DC two-wire power line may carry a current of 10,000 amps
and voltage of 200,000 Volts. Estimate the magnetic field that would be
measured standing at the base of a tower holding up such a line.
- A current in a magnetic field experiences a force. Therefore, it should
be possible to pump conducting liquids by sending a current through the
liquid in an appropriate direction and letting it pass through a magnetic
field. Design (qualitatively) such a pump. This principle is used to pump
liquid sodium (a conductor, but highly corrosive) in some nuclear reactors
where it is used as a coolant. What advantages would such a pump have?
- A typical television tube works by accelerating electrons through an
electrostatic potential and then bending them with a magnetic field as
shown in the figure at the right. If the electrostatic potential difference
used to accelerate the electrons through the anodes is 10,000 Volts, estimate
the maximum strength of the magnetic field needed to control the deflection
of the electron beam. Use your experience with television sets to choose
reasonable parameters for the distances required.
-
| You are assigned the task of building a desk-top sized magnetic spectrometer
for the purpose of measuring the ratio of C 12 to C 14
atoms in a sample in order to determine its age.*
For this problem, let's concentrate on the magnet that will perform
the separation of masses. Suppose that you have burned and vaporized the
sample so that the carbon atoms are in a gas. You now pass this gas through
an "ionizer" that on the average strips one electron from each
atom. You then accelerated the ions by putting them through an electrostatic
accelerator — two capacitor plates with small holes that permit the ions
to enter and leave. The two plates are charged so that they are at a voltage
difference of DV Volts. The electric field produced by charges on the capacitor
plates accelerate the ions to an energy of qDV. These are then introduced
into a nearly constant, vertical magnetic field. (See the figure below.)
If we ignore gravity, the magnetic field will cause the charged particles
to follow a circular path in a horizontal plane. The radius of the circle
will depend on the atom's mass. (Assume the whole device will be placed
inside a vacuum chamber.)
|
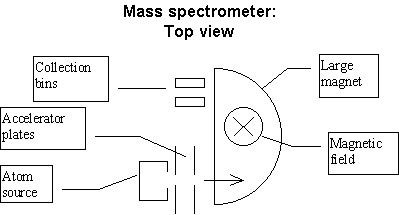 |
Answer three questions about the design.
(a) We would like not to use too high a voltage. If DV is 1000 Volts,
how big magnetic field would we require to have a plausible "table-top-sized"
instrument? Is this a reasonable magnetic field to have with a table-top
sized magnet?
(b) Do the C 12 and C 14 atoms hit the collection
plate far enough apart? (If they are not separated by at least a few millimeters
at the end of their path we will have trouble collecting the atoms in separate
bins.)
(c) Can we get away with ignoring gravity? (Hint: Calculate the time it
would take the atom to travel its semi-circle and calculate how far it
would fall in that time.)
| |
* C 14 is a radioactive isotope of
Carbon that behaves chemically almost identically to its more common but
slightly lighter sibling, C 12 . The amount of C 14 in
the atmosphere stays about constant since it is being produced continually
by cosmic rays. Once carbon from the air is bound into an organic substance,
the C 14 will decay with half of them vanishing every 5730 years.
The ratio of C 14 to C 12 in an organic substance
therefore tells how long ago it died.
-
| A conducting rod slides at a uniform velocity v along a pair of conducting
rails as shown in the figure below. The rod and the rails are in a uniform
magnetic field B pointing into the page as indicated. The rails are separated
by a distance D and the rod has a resistance R. (The resistance of the
rails can be ignored.)
(a) Find the magnitude of the EMF induced across the rod. In what direction
does current flow in the rod?
(b) Find the force required to keep the rod moving to the right with a
constant speed. (Neglect friction.)
(c) Compare the rate at which work is done by the force (Fv) with the rate
at which heat is generated in the circuit (I 2 R).
(d) You want to use the above device as part of your design of an exercise
machine in which a person exercises by pushing the bar back and forth.
If the person can be expected to push the bar with an average speed of
4 m/s, what should the resistance be if the person is to do work at an
average rate of 200 W?
(e) How many Calories would a person burn up working on your machine for
20 minutes?
|
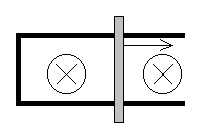 |
- Suppose you are heating a cup of water for tea in a microwave. Assume
that all the energy produced by the microwave goes into heating the water.
Use your best estimate of the time it takes to boil the water to get an
estimate of the power of the microwave in Watts.
Modern Physics
- In the Millikan oil drop experiment, an atomizer (a sprayer with a
fine nozzle) is used to introduce many tiny droplets of oil between two
oppositely charged parallel metal plates. Some of the droplets pick up
one or more excess electrons. The charge on the plates is adjusted so that
the electric force on the excess electrons exactly balances the weight
of the droplet. The idea is to look for a droplet that has the smallest
electric force and assume that it has only one excess electron. This lets
the observer measure the charge on the electron. Suppose we are using an
electric field of 3x10 4 N/C. The charge on one electron is
about 1.6x10 -19 C. Estimate the radius of an oil drop for which
its weight could be balanced by the electric force of this field on one
electron.
- Assume that a 100-W sodium-vapor lamp radiates its energy uniformly
in all directions. The wavelength of the light is 589 nm.
(a) At what rate are photons emitted from the lamp?
(b) At what distance from the lap will the average flux of photons be 1
photon/cm 2 -s)?
|

