1) A long wire is oscillating transversely so that its displacement
has the equation y(x,t) = A cos (k0x - w0t)
where A = 12 millimeters, k0 = p
m-1, and w0 = 100 p
s-1. The string has a density of 1 g/m.
(a) With what speed is the wave moving down the wire?
(b) What is the maximum velocity of a piece of the wire?
(c) What is the tension of the wire?
2) In the four pictures labeled (A)-(D) below are shown snapshots of
waves on a long, taut string. The dashed line shows a picture of a part
of the string at the time t=0. The solid line is a picture at a time a
little bit later. Each of these pictures looks the same at t=0, but the
results differ because the parts of the string have different velocities
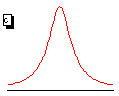
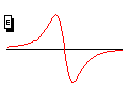
at t=0 in each case.
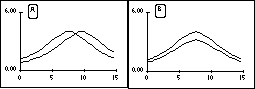 
For each of the four cases above, select one of the six patterns below
as the correct velocity pattern to lead to the solid line displayed. (Note
the arrows indicate mainly direction. Their lengths are scaled somewhat
in proportion to their magnitude, but not strictly so.)
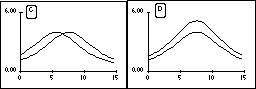
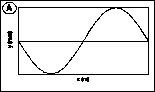
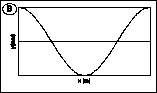
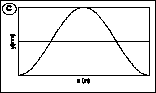
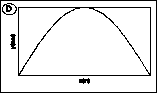
3) The graphs below may represent either a picture of the shape of a
wave on a string at a particular instant in time, t1,
or the transverse (up and down) velocity of the mass points of that string
at that time. Depending on what they are, the wave on the string may be:
(a) a right going traveling wave
(b) a left going traveling wave
(c) a standing wave growing in amplitude at time t1
(d) a standing wave shrinking in amplitude at time t1
For each of the following cases, decide what the wave is doing and choose
one of the four letters (a)-(d).
3.1 Graph A is a graph of the string's shape and graph B is a graph
of the string's velocity.
3.2 Graph A is a graph of both the string's shape and the string's velocity.
3.3 Graph B is a graph of the string's shape and graph A is a graph of
the string's velocity.
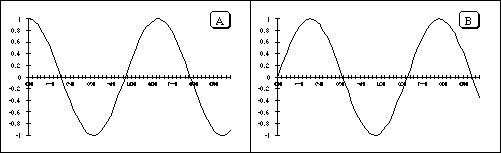
4) A transverse wave pulse is traveling in the positive x direction
along a long stretched string. The origin is taken at a point on the string
which is far from the ends. The speed of the wave is v (a positive number).
At time t=0, the displacement of the string is described by the function
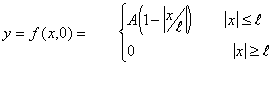
(a) Construct a graph that portrays the actual shape of the string at
t=0 for the case 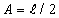 . .
(b) Sketch a graph of the wave form at the following times
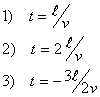
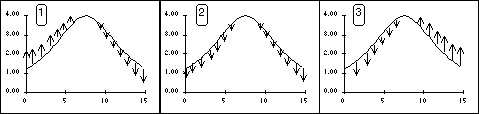
5) The picture below shows a snapshot of a piece of a wave at a time
t=0. Make four copies of this picture and sketch what each pulse would
look like at a slightly later time (a time small compared to the time it
would take the pulse to move a distance equal to its own width but large
enough to see a change in the shape of the string) for the following four
cases:
1) The pulse is a traveling wave moving to the right.
2) The pulse is a traveling wave moving to the left.
3) The pulse is a standing wave whose amplitude is growing.
4) The pulse is a standing wave whose amplitude is shrinking. |
 |
On each picture draw arrows to show the velocity of the marked points
at time t=0.
6) In the figure below are shown graphs which could represent properties
of pulses on a stretched string. For the situation and the properties (a)
- (e) below, select which graph provides the best representation of the
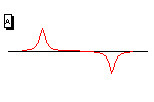
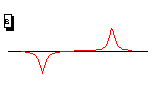
given property. If none of the graphs are correct, write "none".
Two pulses are started on a stretched string. At time t=t0 ,
an upward pulse is started on the right that moves to the left. At the
same instant, a downward pulse is started on the left that moves to the
right. At t0 their peaks are separated by a distance
2s. The distance between the pulses is much larger than their individual
widths. The pulses move on the string with a speed v0
. The scales in the graphs are arbitrary and not necessarily the same.
(a) Which graph best represents the appearance of the string at time
t0 ?
(b) Which graph best represents the appearance of the string at a time 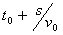 ? ?
(c) Which graph best represents the appearance of the string at a time 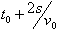 ? ?
(d) Which graph best represents the velocity of the string at a time 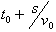 ? ?
(e) Which graph best represents the appearance of the string at a time 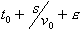 where e is small compared to s/v0
?
where e is small compared to s/v0
?
7) Discuss the physical meaning and content of the wave equation for
the motion of a string of mass density m
stretched with a tension T:
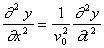
8) A long taut spring is started at a time t=0 with a pulse moving
in the +x direction in the shape given by the function f(x) with
(The units of x and f are in centimeters.)
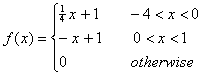
(a) Draw a labeled graph showing the shape of the string at t=0.
(b) If the mass density of the string is 50 grams/meter and it is under
a tension of 5 Newtons, draw a labeled graph that shows the shape and position
of the string at a time t = 0.001 s.
(c) Write the solution of the wave equation that explicitly gives the displacement
of any piece of the string at any time.
(d) What is the speed of a piece of string that is moving up after the
pulse has reached it but before it has risen to its maximum displacement?
What is its speed while it is returning to its original position after
the pulse's peak has passed it?
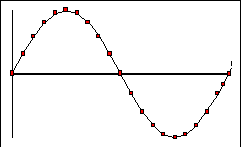
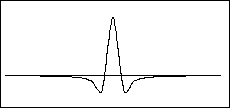
9) In the figure below is shown a picture of a string at a time t1.
The pieces of the string are each moving with velocities which are indicated
by arrows in the picture. (The vertical displacements are small and don't
show up in the picture.) 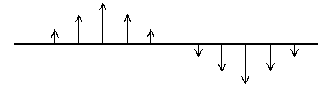
Below are shown five graphs which could give the shape of the string
at the instant for which the velocities are displayed above. (Note:
the vertical scale magnifies the displacement by a factor of 100.)
On your paper, place the letters A - E. Next
to these letters, indicate for the graphs labeled by those letters, whether
the string is moving as a
(L) left-traveling wave
(R) right traveling wave
(S+) a standing wave increasing in amplitude
(S-) a standing wave decreasing in amplitude
(N) none of the above.
10) In the first section of the course, we have analyzed the motion
of a mass on a spring and the motion of a taut string. Discuss these two
systems, explaining similarities and differences, and give an equation
of motion for each.
| 11) A physics professor is demonstrating the motion of waves on a long,
taut spring. He is holding the spring at one end and will move it so the
spring will move back and forth on the floor. The spring is rigidly connected
to a metal rod at its other end. The spring is under a tension T and it
has a mass density m. The professor starts a
triangular pulse moving towards the right as shown in the figure below.
The pulse is triangular and is not symmetric. The figure is shown
at a time t0. |
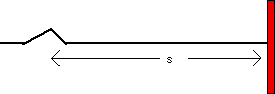 |
(a) Calculate the time t it will take the
peak of the pulse to reach the wall (to travel a distance s).
(b) What will the spring look like at the time t0 + t?
Draw a carefully constructed and labeled diagram to show what it looks
like and how you got your result.
(c) What will the spring look like a bit later say at a time t0
+ 2t? What is responsible for this result?
(d) The width of the pulse is 0.5 m. If the tension in the spring is 5
N and it has a mass density of 0.1 kg/m, how much time did the professor
take to generate the pulse?
12) A guitar string having a mass density of m
is stretched to a length L between its frets and is under a tension T.
(a) What is the speed of small amplitude waves on the string?
(b) If the string is oscillating in a mode which looks like the picture
on the right, find the frequency (in cycles per second) of the oscillation.
(c) What is the frequency if m = 10 g/cm, L
= 1 m, and T = 100 N? |
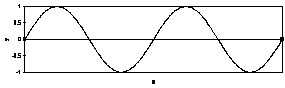 |
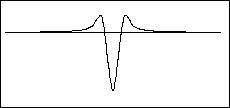
13) The next set of four questions concern the motion of a pulse on
a long taut string. We will choose our coordinate system so that when the
string is at rest it is along the x axis of the coordinate system. We will
take the positive direction of the x axis to be to the right on this page
and the positive direction of the y axis to be up. Ignore gravity.
A pulse is started on the string moving to the right. At a time t0
a photograph of the string would look like figure A below. A point on the
string to the right of the pulse is marked by a spot of paint.
For each of the items below, identify which figure above would look
most like the graph of the quantity. (Take the positive axis as up.) If
none of the figures look like you expect the graph to look, write N.
13.1. The graph of the y displacement of the spot of paint as a function
of time.
13.2. The graph of the x velocity of the spot of paint as a function of
time.
13.3. The graph of the y velocity of the spot of paint as a function of
time.
13.4. The graph of the y component of the force on the piece of string
marked by the paint as a function of time.
14) The next four problems concern the period of oscillation of a standing
wave on a string. Assume that the fundamental mode of oscillation of the
string has a period T0. For each of the changes described below,
give the factor by which the period changes. For example, if the change
described resulted in a period twice as long, you would put the number
"2" on your answer sheet. Do not cumulate changes. That is, before
each change, assume you are back at the original starting situation.
14.1 The mass density of the string is doubled.
14.2 The wave length of the starting shape is divided by three.
14.3 The amplitude of the oscillation is doubled.
14.4 The tension of the string is halved.
15) Consider two physical systems: System A is a mass hanging
from a light spring fixed at one end to a ringstand on a table above the
floor; System B is a long spring of uniform density held under tension
and able to move transversely in a horizontal plane.
1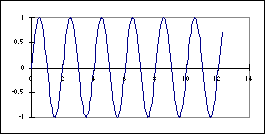
|
In the figure at the left are shown three graphs labeled #1, #2, and
#3, with unmarked axes. They could represent many quantities in the physical
systems A and B.
For the 5 physical quantities below, indicate which of the graphs could
be obtained for the system indicated.
If more than one graph applies, give all the possible choices.
If none applies, write N.
|
2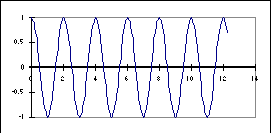
|
(a) The height of the mass hanging from the spring (system A) above
the ground as a function of time for some time interval after the mass
has been set into oscillation.
(b) The transverse displacement from equilibrium of some portion of the
long spring (system B) as a function of position at a particular instant
of time while it is carrying a harmonic wave.
(c) The velocity of the mass hanging from the spring (system A) as a function
of time given that its displacement from equilibrium as a function of time
is given by graph #1.
(d) The transverse velocity of a small piece of the long spring (system
B) as a function of time as a single pulse moves down the spring.
(e) The velocity of a small piece of the long spring (system B) as a function
of time given that its displacement from equilibrium as a function of time
is given by graph #2. |
3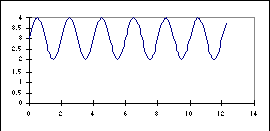
|
|
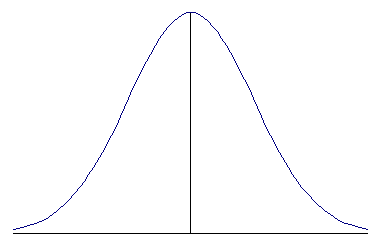
16) The wave equation 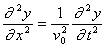
is often used to describe the transverse displacement of waves on a
stretched spring. Explain the meaning of each of the elements of this equation
with reference to the physical spring and discuss under what circumstances
you expect it to be a good description.
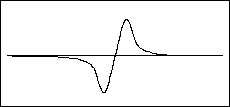
| 17) The picture at the right shows the shape of a pulse on a stretched
spring at the time t=0. The displacement of the spring from its equilibrium
position at that time is given by
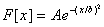
|
 |
The pulse is moving in the positive x direction
with a velocity v0.
(a) Sketch a graph showing the shape of the spring at a later time,
t = t0. Specify the height and position of the peak in
terms of the symbols given.
(b) Write an equation for the displacement of any portion of the spring
at any time, y[x,t].
(c) Sketch a graph of the velocity of the piece of the spring at the position
x = 2b as a function of time.
18) A physicist observes the motion of a plucked guitar string of length
L. She proposes that the following function of position and time is a possible
description of the displacement of the string:
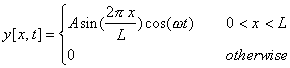
(a) If the speed of transverse waves on the guitar string is v0,
can she choose any angular frequency, w,
she wants or does it have to be some particular frequency? How do you know?
(b) If her equation is correct, which piece of the string moves the fastest?
What is its maximum velocity?
19) A long elastic string is attached to a distant wall. A demonstrator
holds the end of the string and quickly moves it up once and then back
down to the original position, producing a pulse traveling towards the
wall as shown.
The demonstrator can make various changes before doing the experiment
a second time. These include:
1) Moving his hand more quickly (but still only up and down once and
still by the same amount).
2) Moving his hand more slowly (but still only up and down once and still
by the same amount).
3) Moving his hand a larger distance but up and down in the same amount
of time.
4) Moving his hand a smaller distance but up and down in the same amount
of time.
5) Using a heavier string, under the same tension.
6) Using a lighter string, under the same tension.
7) Using a string of the same density, but decreasing the tension.
8) Using a string of the same density, but increasing the tension.
For each of the following situations, which of the actions 1-8, taken
by itself, will produce the desired result? For some of the situations,
more than one answer may be correct. If so, give them all. (Do not
consider the result of combining more than one of the actions 1-8.)
(a) The demonstrator wants to produce a pulse that has the same height
as the original pulse but is wider.
(b) The demonstrator wants to produce a pulse that takes a longer time
to reach the wall.
20) Consider the equation 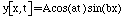
Let x represent some position and t represent time.
(a) Describe a physical situation represented by this equation. As part
of your description include a sketch and a written description. Indicate
what y and x correspond to in the situation you describe.
(b) How, if at all, would the physical situation you described in part
A be different if a were twice as large? Explain how you determined
your answer.
(c) How, if at all, would the physical situation you described in part
A be different if b were twice as large? Explain how you determined
your answer.
| 21) The figure at right is taken from a popular standard
textbook. In the first column is shown a pulse approaching and reflecting
from a fixed end. In the second column is shown a pulse approaching and
reflecting from a free end (ring sliding on a frictionless rod). At least
six (6!) of the figures are incorrect. State which and explain why. (Hint:
The second edition of the book fixed most of the problems by making the
pulses symmetric.) |
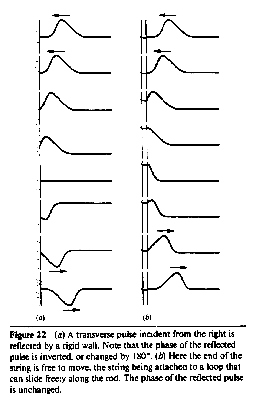 |
22) A nylon guitar string has a linear mass density of 7.2 g/m and is
under a tension of 150 N. The fixed supports are 90 cm apart, The string
is vibrating in the standing wave pattern of a pure second harmonic, that
is, there are two nodes in addition to the endpoints. Calculate (a) the
speed, (b) the wavelength, and (c) the frequency of the component waves
whose superposition gives rise to this vibration.
23) Compare and contrast the behavior of (a) the mass of a mass-spring
system oscillating in simple harmonic motion and (b) an element of a stretched
string through which a traveling sinusoidal wave is passing. Discuss from
the point of view of displacement, velocity, acceleration, and energy transfer.
|


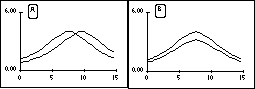

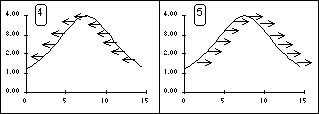


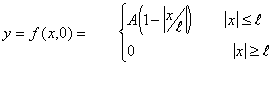
![]() .
.
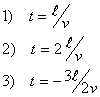

![]() ?
?
![]() ?
?
![]() ?
?
![]() where e is small compared to s/v0
?
where e is small compared to s/v0
? 

![]()
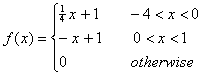
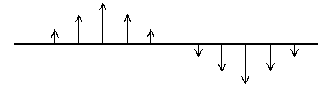
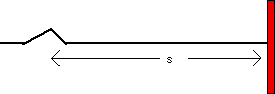





![]()
![]()

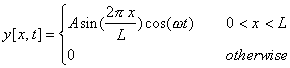
![]()

![]()