1) Consider how the components of a vector in the plane change if I
change the reference point. Suppose I start with a coordinate system with
an origin at O. An arbitrary vector r with coordinates (x,y) specifies
a point in this system. Suppose also that I have another point O' specified
in this coordinate system by a vector A = (a,b). If I change my
origin to O' (without rotating the axes), what would the coordinates be
for the point specified by r?
2) a) A dry ice puck is sliding on the top of the table in the lecture
hall. The table is 3 m long by 2 m deep. Take the left corner closest to
you as the origin of a coordinate system and take the positive x axis to
run along the edge closest to you, and take the positive y axis to run
back towards the blackboard.
A timer is started. At time t = 1.4 s, I release a dry ice puck at the
point r0 = (0.5 m) i + (0.5 m) j with a
velocity v = (1.0 m/s) i + (0.3 m/s) j. The puck moves
with this constant velocity until it falls off the table. Write an equation
for the position vector of the puck, r(t), for the time while it
is on the table. (You do not have to calculate when it falls off the table.)
b) An object moving on the lecture table described above moves as a
function of time so that its position at time t is given by
r(t) = A sin wt i + B cos wt
j
where A = 0.5 m, B = 1.0 m, and w= 1.2 s
-1 . Calculate the velocity and the acceleration of the object as
a function of time. Can you say at what time it will fall of the table?
3) A child is riding a go-cart in a school playground. If we choose
an origin in the center of the playground, the position of the go-cart
as a function of time can be written
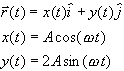
The constant A = 4 m and the constant w =
p s -1 .
(a) Calculate the position of the cart at the times 0, 0.5 s, 1 s, 1.5
s, and 2 s.
(b) Draw a coordinate system representing the playground. Mark the points
you calculated in (a) on your drawing and sketch a plausible path in between
these points. Indicate the direction of the velocity and acceleration vectors
of the cart at the marked points.
(c) Calculate the velocity and the speed of the cart as a function of time.
Is the speed a constant?
4) A child on a merry-go-round is moving in a circle with radius R at
a speed v. For each of the problems below, draw a separate diagram of the
system as seen from above and display the appropriate vectors. Take the
origin of your coordinate system to be at the center of the merry-go-round.
(a) Show the position vectors when the child's (x,y) coordinates are
A = (0,R), B = (R,0), and C = (-R, R)/Sqrt(2).
(b) Show the position vectors A', B', and C' at a
brief time after the child has been at A, B, and C
respectively. (c) Show the change in position vectors delta A =
A'-A, delta B = B'-B, and delta C = C'-C.
(d) Show the vectors representing the velocity of the child when it is
at each of the points A, B, and C. How are these related
to the vectors in the previous part?
(e) Repeat the previous parts with the velocity and acceleration replacing
the position and velocity.


![]()