1) A crate is pulled along a horizontal surface at constant velocity
by an applied force Fa that makes an angle q
with the horizontal. The coefficient of kinetic friction between the crate
and the surface is m. Show that the magnitude
of Fa is a minimum when the angle q
is given by tan-1 m.
2) Suppose you are sitting in a car that is speeding up. Draw well-separated
force diagrams of the following objects:
- your own body;
- the seat in which you are sitting (apart from the car);
- the car (apart from the seat);
- the road surface where the tires and the road interact.
Assume the car has rear wheel drive.
- Describe each force in words; show larger forces with longer arrows.
- Identify the third law pairs.
- Explain carefully in your own words how the force imparting acceleration
to the car originates.
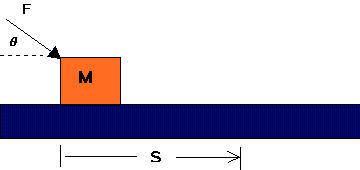
3) A block of mass M is pushed along a frictionless table
by a force F for a distance s as shown in the figure
at the right. The force is inclined to the horizontal at an angle q.
When it reaches s, the force is removed. The block starts from rest
at clock time 0:00. Express your answers in terms of M, F
(= the magnitude of F), q, and s.
(a) Calculate the acceleration of the block during the time the force
is acting.
(b) At what time will the box have moved through the distance s?
Find the object's velocity at that time.
(c) Calculate the change in the object's kinetic energy using the work-energy
theorem and show that it gives the same result you would calculate using
change in the object's velocity.
(d) What is the object's change in momentum from the time it starts to
the time it reaches s?
(e) If the same force pushed a larger mass for the same distance, would
the object have more or less kinetic energy than the original box? What
about momentum? Give a qualitative explanation for your results that makes
them plausible.
4) Newton's first law states that an object will move with a constant
velocity if nothing acts on it. This seems to contradict our everyday experience
that all moving objects come to rest unless something acts on it to keep
it going. Does our everyday experience contradict one of Newton's Laws?
If it does not, explain the apparent contradiction. If it does, explain
why we bother to teach Newton's first law anyway.
5) A worker is pushing a cart along the floor. At first, the worker
has to push hard in order to get the cart moving. After a while, it is
easier to push. Finally, the worker has to pull back on the cart in order
to bring it to a stop before it hits the wall. The force exerted by the
worker on the cart is purely horizontal. Take the direction the worker
is going as positive.
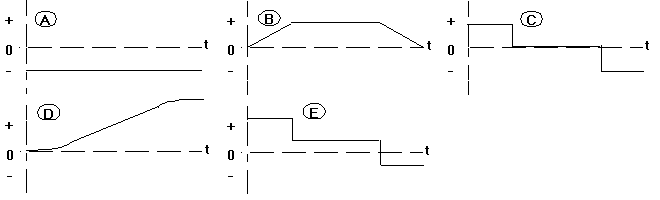
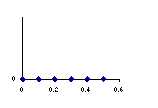
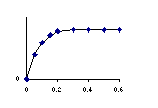
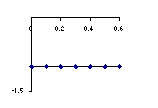
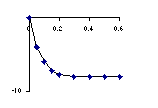
Below are shown graphs of some of the physical variables of the problem.
Match the graphs with the variables in the list below. You may use a graph
more than once or not at all. (Note: the time axes are to the same scale,
but the ordinates {"y axes"} are not.)
(a) friction force
(b) force exerted by the worker
(c) net force
(d) acceleration
(e) velocity.
6) You are pushing on a block that is resting on the table.
(a) You press on the block but not hard enough to start it moving. What
are the forces acting on the block? (Be sure to specify the type of force
and the object causing each force.) Wherever you can, compare the magnitudes
of forces. Give a brief explanation for how you know each of the results
you state.
(b) You press a bit harder and the block begins to move. After a moment
of starting up, you press so that the block is moving with a constant velocity.
For the time while the block is moving with a constant velocity have any
of the comparisons you stated in (a) changed? Which ones? Have any of the
forces changed? Which ones?
(c) Suppose the block has a mass of 0.4 kg and the coefficient of friction
between the block and the table is 0.3. What force will you have to use
to keep it going at a constant velocity of 0.2 m/s? (You may take g = 10
N/kg.)
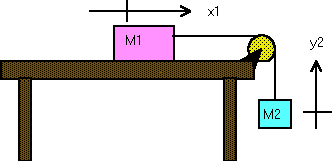
| 7) A block of mass M1 is sitting on a frictionless
table. It is connected by a massless string over a massless
and frictionless pulley to another block of mass M2.
(a) Build free-body diagrams for each of the masses and write equations
of motion for each object. Use the coordinate x1 shown in the
figure for the position of mass M1 and coordinate y2
shown in the figure for the position of mass M2.
(b) Use these equations of motion to obtain the acceleration of the two
objects. Explicitly state any conditions that you are applying to solve
the equations.
|
 |
8) A block of mass M1 is sitting on a table with a block
of mass M2 sitting on top of it. Attached to the bottom block
is a ring and a string is attached to the ring. The string is pulled with
a tension T. The coefficient of friction between block 1 and the table
is m1, and the coefficient of friction
between block 2 and block 1 is m2.
(Ignore the difference between static and kinetic friction.)
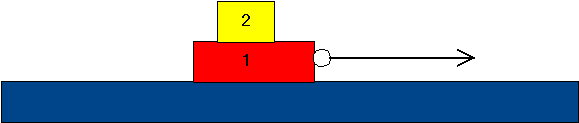
(a) For one given value of T the blocks accelerate together.
- Draw free body diagrams for each of the blocks.
- Calculate the acceleration of the blocks.
- What can you say about the magnitude and direction of the various frictional
forces in the system?
(b) For a second, larger, value of T, the first block continues to accelerate,
but the second block begins to slip back on the first block.
- How do the free body diagrams for the two blocks change from the case
above?
- Calculate the acceleration of block 2.
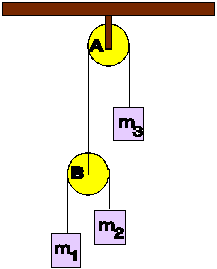
| 9) The system shown in the figure is initially motionless and the pulleys
are of negligible mass.
(a) Write free-body diagrams for each mass and their equations of motion.
(b) Show that the accelerations of the three objects are related by
a1 + a2 + 2 a3 = 0
(c) Suppose m2 = 2 m1. When the system is released,
it is found that body 1 remains stationary. What is the tension in the
string supporting body 1?
(d) Find the magnitude and direction of the acceleration of body 2, of
pulley A, of body 3, and the tension in the string supporting pulley A.
(e) What is the mass of body 3?
|
 |
10) Write an essay about Newton's second law. In your essay, make sure
you state the law in words and equation form. For the equation you give,
explain carefully the meaning of each symbol in the equation. Also include
a brief discussion of "what the equation is good for", that is,
how you might use it in practice.
11) A physics student is pulling a small wooden crate across a wooden
floor using a rope tied to a ring which is attached to the box.
The box has a mass m, the student has a mass M, and the
coefficient of friction between the box and the floor is m.
(Ignore the difference between static and kinetic friction.) The angle
between the rope and the horizontal is q.
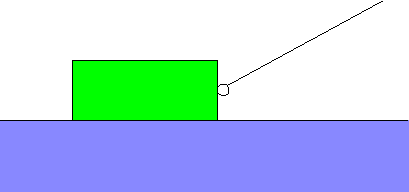
(a) What force does the student have to exert on the rope to keep the
box moving at a constant speed?
(Express your answer in terms of the relevant given symbols.)
(b) If q = 30º, m = 20 kg,
M = 80 kg, m = 0.4, and g = 10
N/kg, find the tension in the rope.
(c) State one approximation you have made in order to make this problem
more easily solved. (By "approximation" I mean some simplification
that has been made or real-world effect that is being ignored. I do not
mean that one of the numbers given might be a bit wrong.)
| 12)

|
A boy with a mass m = 50 kg is skating on a flat, level sidewalk.
He can get himself up to a speed V = 6 m/s. If he then just coasts,
he travels a distance d = 10 m before coming to a stop.
(a) Find the coefficient of friction between the boy and the sidewalk.
(b) He approaches a part of the sidewalk which rises at an angle q
= 30º to the ground for a distance D = 5 m before leveling
out. If he reaches the rise going at his maximum speed will he be able
to coast to the top? Explain.
|
13) Two blocks, A and B, of masses MA and MB
respectively, are tied together with a rope, R, of mass M. The small
block, B, is being pushed with a constant horizontal force as shown
below. Assume that there is no friction between the blocks and the table,
and that the blocks have already been moving for a while at the instant
shown and their relative position is not changing. The "push"
is exerting a force F on block B.
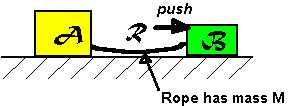
(a) Will block B be moving at a constant speed or will it be
speeding up? Explain your answer.
(b) Draw careful free-body diagrams specifying all the forces acting on
the three objects in the problem.
(c) Calculate the acceleration of the system.
| 14) A large heavy cart of mass M is sitting on a table at rest.
The cart has wheels and rolls on the table with negligible friction. A
smaller block of mass m is tossed so it lands on top of the cart
at time t = 0 . At this instant, when the block first
touches the cart, the cart is at rest and the block is moving with a velocity
v0 as shown in the figure below. The coefficient of friction
between the cart and the block is m.
|
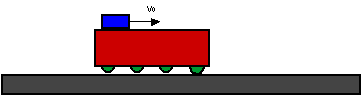 |
(a) Assume that the block slides on the cart for a while before being
brought to a stop relative to the cart. (Assume the block is not moving
fast enough to slide off the end of the cart.) Describe what happens to
the cart and the block.
(b) While the block is sliding on the cart, draw separate free-body diagrams
for the cart and the block, showing all forces that act on each one.
(c) Is the momentum of the system consisting of the cart + block conserved?
Explain.
(d) Find the final velocity of the cart-block system after the block has
come to rest on top of the cart. Express your answer in terms of the symbols
given in the description of the problem. |
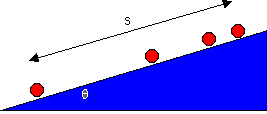
| 15) The figure to the right shows a multiple-exposure photograph of
a ball rolling up an inclined plane. (The ball is rolling in the
dark, the camera lens is held open, and a brief flash occurs every 3/4
sec four times.) The left-most ball corresponds to an instant just after
the ball was released. The right-most ball is at the highest point the
ball reaches.
(a) Copy this picture and, at each ball, draw an arrow to indicate the
velocity of the ball at the instant when it was at that point in space.
Explain what is happening ("tell the story" of the picture).
(b) For the instant of time when the ball is at the second position shown
from the left, draw a free-body diagram for the ball and indicate all forces
acting on it.
(c) If the mass of the ball is m, what is its acceleration?
(d) If the angle q is equal to 30o,
how long is the distance s?
|
 |
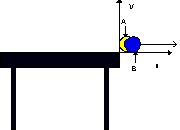
16) Two identical billiard balls are labeled A and B. Maryland
Fats places ball A at the very edge of the table, ball B at the other side.
He strikes ball B with his cue so that it flies across the table and off
the edge. As it passes A, it just touches ball A lightly, knocking it off.
The balls are shown just at the instant they have left the table. Ball
B is moving with a speed v0, ball A is essentially at rest.
(a) Which ball do you think will hit the ground first? Explain your
reasoning.
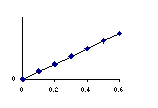
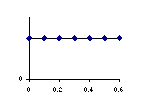
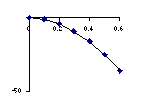
Below are shown a number of graphs of a quantity versus time. For each
of the items below, select which graph could be a plot of that quantity
vs. time. If none of the graphs are possible, write N. The time axes are
taken to have t=0 at the instant both balls leave the table. Use the x
and y axes shown in the figure. For each of the following, which graph
could represent
(b) the x-component of the velocity of ball B?
(c) the y-component of the velocity of ball A?
(d) the y-component of the acceleration of ball A?
(e) the y-component of the force on ball B?
(f) the y-component of the force on ball A?
(g) the x-component of the velocity of ball A?
(h) the y-component of the acceleration of ball B?
|
 |
|
|
|
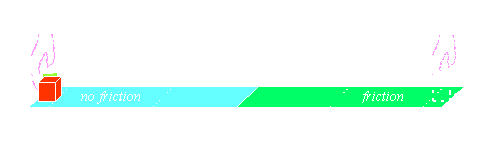
| 17) A hand pushes a 3 kg block along a table from point A to point
C as shown in the figure below. The table has been prepared so that the
left half of the table (from A to B) is frictionless. The right half (from
B to C) has a non-zero coefficient of friction equal to m.
The hand pushes the block from A to C using a constant force
of 5 N. The block starts off at rest at point A and comes to a stop when
it reaches point C. The distance from A to B is 1 meter and the distance
from B to C is also 1 meter.
|
|
|
(a) Describe in words the motion of the block as it moves from A to
C.
(b) Draw a free-body diagram for the block when it is at point P.
(c) What is the direction of the acceleration of the block at point P?
If it is 0, state that explicitly. Explain your reasoning.
(d) Does the magnitude of the acceleration increase, decrease, or remain
the same as the block moves from B to C? Explain your reasoning.
(e) What is the net work done on the object as it moves from A to B? From
B to C?
(f) Calculate the coefficient of friction m. |
18) You and your friends have prepared a large pot of soup to take to
the local homeless shelter. The pot is large two feet high and two feet
in diameter. In order to get it to the shelter, you put the pot in the
back of your friend's pick-up truck, pressed against the back wall (next
to the cab) and against the left wall (on the driver's side). You are pretty
sure that you have to drive carefully so the pot doesn't tip over. Do you
have to be more careful when starting or when stopping? When turning left
or when turning right? Explain your choice.











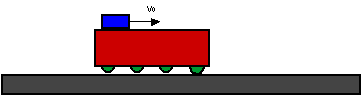



![]()