1) A student makes the following argument: "I can prove a dollar
equals a penny. Since a dime (10 cents) is one-tenth of a dollar, I can
write:
10¢ = 0.1 $
Square both sides of this equation. Since the squares of equals are
equal,
100 ¢ = 0.01 $. Since 100 ¢ = 1 $ and 0.01 $ = 1 ¢ it follows that 1$ = 1
¢."
What's wrong with the argument? | 
|
2) Each of the following equations has been written down by a student
during an examination. Do a dimensional analysis of each equation and explain
why the equation cannot be correct. 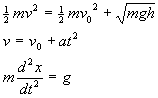
The University of Maryland's mascot is a terrapin (a snapping turtle).
It is represented on campus by a bronze statue in front of the library
named Testudo. Unfortunately, students rub his nose for luck on tests,
and he is beginning to wear out. A sculptor decides to propose a replacement.
She builds a small scale model and discovers she needs 2 kg of bronze.
When she is finished, she finds that she can give it two coats of finishing
polyurethane varnish using exactly one small can of varnish. Her final
statue will be 5 times as big as her model in all dimensions. How much
bronze and how much varnish will she need for the final product?
|
 |
3) In the US we specify how efficiently a car uses gas by citing how
many miles per gallon it gets (MPG). In Europe they cite liters per 100
kilometers (LPK). Note the conversion factors:
- 1 mi = 1.6 km
- 1 gal = 3.8 liters
(a) Does a more efficient car have a larger or smaller MPG number? Explain
how you know.
(b) Does a more efficient car have a larger or smaller LPK number? Explain
how you would know.
(c) If M is the number of miles per gallon a car gets, and L is the number
of liters it takes to go 100 km, find a mathematical equation that lets
you convert from M to L.
4) Two Terrapins (U. of Md. students) decide to go to Jerry's for a
pizza. When they get there they find Jerry's is having a special:
| SPECIAL: |
| one 20" pizza |
$15 (toppings extra) |
| REGULAR PRICE: |
| one 10" pizza |
$5 |
| one 20" pizza |
$18 |
| Raphael goes: "Great! Let's get a large one."
Donatello goes: "Don't be dumb. Let's get three of the small ones
for the same price. That'll give us more pizza and be cheaper."
Raphael goes: "Why would it be a special if it's less pizza than
we could get for regular price? Let's get the large."
Who's right? Which would you buy?
What would the difference be if you were buying them at Ledo's (square
pizzas)?
|
 |
5) A fan is driven by an electric motor which delivers a constant torque
t. Take the axis of rotation and the torque
to be fixed in the z-direction. The air gives a retarding torque which
has the form tair=-w2
where B is a constant and w is the magnitude
of the angular velocity of the fan. Let I be the moment of inertia
of the moving parts of the fan about its axis of rotation.
- Write the equation for the angular motion of the fan which gives the
angular acceleration a =dw/dt.
- Give an argument that the fan will reach a terminal angular velocity,
wT, and give an expression for wT
in terms of the parameters B, I, and t
- What are the dimensions of the parameter B?
- Suppose we consider the geometrical shape of the fan to be fixed, but
change its size, i.e. the radius, R, and the mass, M. These
can be changed independently, for example by changing the material of which
the fan is made. Assume that B depends on the density of air r,
and the radius R, but not on M. Using dimensional analysis,
how does B depend on r and R?
- Why is it reasonable to assume that B does not depend on M?
- Suppose we build a second fan, exactly like the first except the radius
is 2 R instead of R, and the motor gives a torque tbigger
instead of t. If these two fans are to have
the same terminal angular velocity, what must the ratio tbigger/t
be?
Contributed by Richard Prange, University of Maryland
|
 |
6) Each of the mathematical expressions below was given by a student
on his or her way to the solution of an exam problem. Assume each of the
symbols stands for what we use them for in this class (as indicated in
each line). If you believe the equation given could possibly be a correct
physical equation, write Y. If you think that it could not possibly
be a correct physical equation, write N and give a brief explanation of
why you think so.
(a) 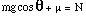 (mass, gravitational
field strength, coefficient of friction, normal force) (mass, gravitational
field strength, coefficient of friction, normal force)
(b) 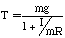 (tension, mass, gravitational
field strength, moment of inertia, radius) (tension, mass, gravitational
field strength, moment of inertia, radius)
(c) 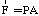 (force, pressure,
area) (force, pressure,
area)
(d) 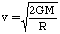 (velocity, universal
gravitational constant, mass, radius) (velocity, universal
gravitational constant, mass, radius)
|



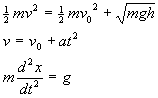



![]() (mass, gravitational
field strength, coefficient of friction, normal force)
(mass, gravitational
field strength, coefficient of friction, normal force) ![]() (tension, mass, gravitational
field strength, moment of inertia, radius)
(tension, mass, gravitational
field strength, moment of inertia, radius) ![]() (force, pressure,
area)
(force, pressure,
area) ![]() (velocity, universal
gravitational constant, mass, radius)
(velocity, universal
gravitational constant, mass, radius)![]()