
Teaching Physics with the Physics Suite
Home | Action Research Kit| Sample Problems | Resources | Product Information
Problems Sorted by Type | Problems Sorted by Subject | Problems Sorted by Chapter in UP
 |
Teaching Physics with the Physics Suite
Home | Action Research Kit| Sample Problems | Resources | Product Information |
Problems Sorted by Type | Problems Sorted by Subject | Problems Sorted by Chapter in UP |
A long taut spring is started at a time t=0 with a pulse moving in the +x direction in the shape given by the function f(x) with (The units of x and f are in centimeters.)
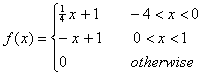
Not finding what you wanted? Check the Site Map for more information.
Page last modified October 30, 2002: O22