
Teaching Physics with the Physics Suite
Edward F. Redish
 |
Teaching Physics with the Physics Suite Edward F. Redish |
In this problem you will try to make sense of how we use signs to specify direction in our specification of motion. Consider a small cart confined to move along a one-dimensional track as shown in the figure below. We specify the position of the cart by using the x-coordinate shown. The position of the cart is taken to be specified by the value of x that the little arrow on the front of the cart points to.
![]()
We specify the cart's position along the track by using a vector
![]() .
.
The i-hat indicates the positive x direction, while the coordinate x specifies the distance from the origin. If it is positive it is on the right of the origin, if negative it is on the left.
We describe our motion in terms of position, velocity, and acceleration. Each can independently be positive, negative, or zero.
(a) Define velocity and acceleration for the cart in terms of our vector notation.
(b) There are 27 different combinations (!) of +/-/0 for position, velocity, and acceleration (= 3 x 3 x 3) . Are all of these possible? For each case that is possible, give a brief description of where the car is and how it is moving, and sketch a bit of the graphs for position, velocity, and acceleration vs. time. For each case that is not possible, give an explanation of why it isn't. (Hint: Paying attention to the patterns that develop may speed up the task.)
Solution
(a) The average velocity and average acceleration are defined in vector notation by

The arrows simply mean that we are considering the directions as well as the coordinates in our description. If there is motion in another direction, say y, the vector equations would simply stand for a set of equations such as
 .
.
If we want to consider the position, velocity, and acceleration at a particular instant (as in part (b) of this problem) we make the time intervals very short and write
 .
.
But we have to be careful! We can think about a position at a particular instant of time, but we have to remember to think about a velocity about referring to what are essentially two instants -- one a bit before the time we are considering and one after. We have to do this in order to see the change in the position. Similarly, we need to be thinking about acceleration as involving a change in velocity so, even for an instantaneous acceleration, we need to think about the velocity at two instants -- one a bit before the time we are considering and one after. We have to do this in order to see the change in the velocity.
(b) Considering the position, velocity, and acceleration of the cart at an instant, all of the combinations are possible. If the cart were your car, the axis were your street, and we take the origin at your front door, you can be anywhere on the street. This is what the position tell you. You can be traveling in either direction or be stopped wherever you are. This is what the velocity tells you. Wherever you are or however you are moving, you can be speeding up, slowing down, or keeping a constant velocity. This is what the acceleration tells you.
The descriptions of the individual cases are given in the table below. The values being referred to occur at t = 0 in the graphs.
| x | v | a | Description | Graphs |
|---|---|---|---|---|
0
|
0 |
0 |
At the origin at rest. Staying stationary |  |
0
|
0 |
+ |
At the origin at rest. Starting to move to the right. |  |
0
|
0 |
- |
At the origin at rest. Starting to move to the left. |  |
0
|
+ |
0 |
Moving past the origin to the right at a constant speed. |  |
0
|
+ |
+ |
Moving past the origin to the right and speeding up. |  |
0 |
+ |
- |
Moving past the origin to the right and slowing down. |  |
0 |
- |
0 |
Moving past the origin to the left at a constant speed. |  |
0 |
- |
+ |
Moving past the origin to the left and slowing down. |  |
0 |
- |
- |
Moving past the origin to the left and speeding up. |  |
+ |
0 |
0 |
On the right side of the origin at rest and staying at rest. |  |
+
|
0 |
+ |
On the right side of the origin at rest starting to move to the right. |  |
+
|
0 |
- |
On the right side of the origin at rest starting to move to the left. |  |
+ |
+ |
0 |
On the right side of the origin moving to the right at a constant speed. |  |
+ |
+ |
+ |
On the right side of the origin moving to the right and speeding up. | 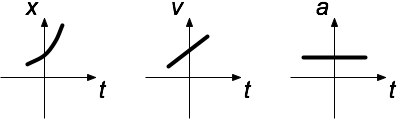 |
+ |
+ |
- |
On the right side of the origin moving to the right and slowing down. |  |
+ |
- |
0 |
On the right side of the origin moving to the left at a constant speed. | 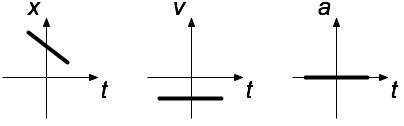 |
+ |
- |
+ |
On the right side of the origin moving to the left and slowing down. |  |
+ |
- |
- |
On the right side of the origin moving to the left and speeding up. |  |
- |
0 |
0 |
On the left side of the origin at rest and staying at rest. |  |
- |
0 |
+ |
On the left side of the origin at rest starting to move to the right. |  |
- |
0 |
- |
On the left side of the origin at rest starting to move to the left. |  |
- |
+ |
0 |
On the left side of the origin moving to the right at a constant speed. |  |
- |
+ |
+ |
On the left side of the origin moving to the right and speeding up. |  |
- |
+ |
- |
On the left side of the origin moving to the right and slowing down. |  |
- |
- |
0 |
On the left side of the origin moving to the left at a constant speed. |  |
- |
- |
+ |
On the left side of the origin moving to the left and slowing down. |  |
- |
- |
- |
On the left side of the origin moving to the left and speeding up. |  |
Some of these examples are quite tricky. Particularly where the velocity is negative. If the velocity is negative, a positive acceleration means that the velocity changes towards the positive so it is getting less negative -- slowing down. If the velocity is negative, a negative acceleration means that the velocity changes towards the negative so it is getting more negative -- speeding up.
Note also that being at the origin does not mean you stay at the origin. You could just be driving past it. Having zero velocity does not mean that you have zero velocity for any finite length of time. You could just be passing through zero velocity (like a ball thrown straight upward at the top of its path).
Page last modified October 17, 2008: K24