Teaching Physics with the Physics Suite Edward F. Redish Home | Action Research Kit| Sample Problems | Resources | Product Information
	Problems Sorted by Type | Problems Sorted by Subject | Problems Sorted by Chapter in UP

A motorized dune buggy is moving along an elliptical track. A picture of the track with a choice of coordinate system is shown in the figure at the top of the next page. Each tic mark along the x and y axes represents a distance of 100 meters. (a) The driver drives around the track three times keeping her speedometer reading at a constant 35 miles per hour. Redraw the ellipse and its coordinate system. During her second circuit of the ellipse, draw onto your picture vectors indicating her position (use a single arrow ®), her velocity (use a double arrow Þ) and her acceleration (use a fat arrow è) when she is at the positions

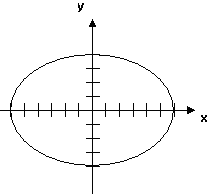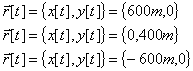
(b) As she begins her fourth circuit round the track, she begins to speed up when she reaches the point {600 m, 0} and continues speeding up at a uniform rate until she reaches the point {-600 m, 0} and is traveling at a speed of 50 mph. Draw another ellipse and draw velocity vectors (use a double arrow Þ) to indicate her velocity when she is a few meters before the point {0, 400 m} and a few meters after that point. Draw her acceleration arrow (use a fat arrow è) when she is at the position {0, 400 m}.

Note to the instructor: Surprisingly, students have a lot of trouble with the position part of this problem. They often forget that a position vector always means the displacement from a particular origin. Perhaps it isn't so surprising. Position vectors are the only ones we use that are tied down -- they can't be put anywhere.

Note also that I have used curly brackets for vectors. Student sometimes get confused by the fact that parentheses have three distinct meanings: grouping in an equation, indicating functional dependence, and setting off a vector.

Not finding what you wanted? Check the Site Map for more information.

Page last modified October 15, 2002: K12