 This work was supported in
part by NSF grants DUE 945 5561 and DUE 965 2877.
This work was supported in
part by NSF grants DUE 945 5561 and DUE 965 2877.
Millikan Award Lecture (1998):
Building a Science of Teaching Physics
 This work was supported in
part by NSF grants DUE 945 5561 and DUE 965 2877.
This work was supported in
part by NSF grants DUE 945 5561 and DUE 965 2877.
Abstract
Individual teachers of college level physics sometimes develop deep insights into how their students learn and what elements of classroom instruction are valuable in facilitating the learning process. Yet these insights rarely persist beyond the individual instructor. Educational methods seem to cycle from one fad to another, rarely cumulating increasingly powerful knowledge in the way scientists expect understanding to grow. In this paper I explore the character of our understanding of the physical world and of teaching about it. The critical factor is using "the culture of science" — the set of processes that allow us to build a community consensus knowledge base. Elements of the beginning of a base for our educational knowledge are discussed and examples given from discipline-based physics education research.
In 1903, Robert Millikan published the first volume of a two volume reform curriculum in introductory physics. In the preface to this volume he makes the following statement: [1]
The most serious criticism which can be urged against modern laboratory work in Physics is that it often degenerates into a servile following of directions, and thus loses all save a purely manipulative value. Important as is dexterity in the handling and adjustment of apparatus, it can not be too strongly emphasized that it is grasp of principles, not skill in manipulation which should be the primary object of General Physics courses.
He goes on to discuss the character of his new course in which lectures and laboratories are closely entwined. Priscilla Laws has already discussed Millikan’s laboratory-based course in some detail in her 1996 Millikan Lecture [2] so I will not go into detail here. Fourteen years later, in 1917, Millikan published a small volume entitled The Electron.[3] This volume includes a discussion of Millikan’s determination that it makes sense to talk about the electron as having a fixed charge:
Here, then, is direct, unimpeachable proof that the electron is not a ‘statistical mean,’ but that rather the electrical charges found on ions all have either exactly the same value or else small exact multiples of that value.
The implications of Millikan’s comments on the nature of the electron have been included in nearly every introductory physics text since soon after the results were published. Indeed, the issue as to whether the electron’s charge may assume continuous or discrete values is almost never considered as a possibility, his result is so well ingrained. Yet few people today know of Millikan’s reform curriculum and his description of the issues it is meant to deal with sounds both modern and pertinent. The type of curriculum he developed for college physics has vanished and reappeared only to vanish again with maddening regularity during the nearly 100 years since he proposed it. Melba Phillips said it best when she said: "The trouble with problems in physics education is they don’t stay solved."[4]
What is it that allows us to build our knowledge of physics in a cumulative way while in physics education we seem to be doomed to everlasting cycles of pushing the Sisyphian rock up the hill only to have it roll down again? Why do we never seem to be able to share and pass down to succeeding generations what we learn about physics education? Is there anything we can do to change this unhappy situation or is it part of the fundamental character of education and of human beings?
In order to understand the elements needed for us to cumulate knowledge about physics education, we need to consider what it is about physics (and about science in general) that leads to successful accumulation of knowledge in those fields. In this paper I begin with a discussion of the nature of scientific knowledge and consider those elements that lead to accumulation of knowledge. I then discuss the embedding environment of physics education — the general principles of learning theory that have been developed by cognitive scientists and education theorists. Next, I present examples of what sort of knowledge has been obtained from physics education research. The paper concludes with a discussion of how a science-like physics education research enterprise fits into physics as a whole and the value it can have for the community of physicists. Throughout, I explicitly discuss those elements which are controversial, confusing, or commonly misconstrued.
We often say that the goal of science is to discover the laws of nature. This is not quite precise enough for our purposes. It’s better to say that we are trying to create the best way of thinking about the world that we can. This places the knowledge firmly where it really resides — in the head of the scientist.
A good metaphor for the process of science is the building of a map. A map of the world should not be mistaken for the world,[5] but it can nonetheless be of great value in getting around. What is perhaps most important about the scientific map of the world is that it is more than just the collection of the maps of individual scientists. The culture of science includes the continual interaction, exchange, evaluation, and criticism we make of each other’s views. This produces a kind of emergent phenomenon I refer to as a community consensus knowledge base or more briefly, a community map. I visualize this as an idealized atlas of science. Just as an atlas contains many individual charts, the atlas of science contains many distinct coherent but incomplete areas of knowledge. These areas are supposed to agree where they overlap, but it is not clear that the entire universe can be encompassed in a single map.[6] No single individual, no matter how brilliant, contains a map identical to this community consensus map.
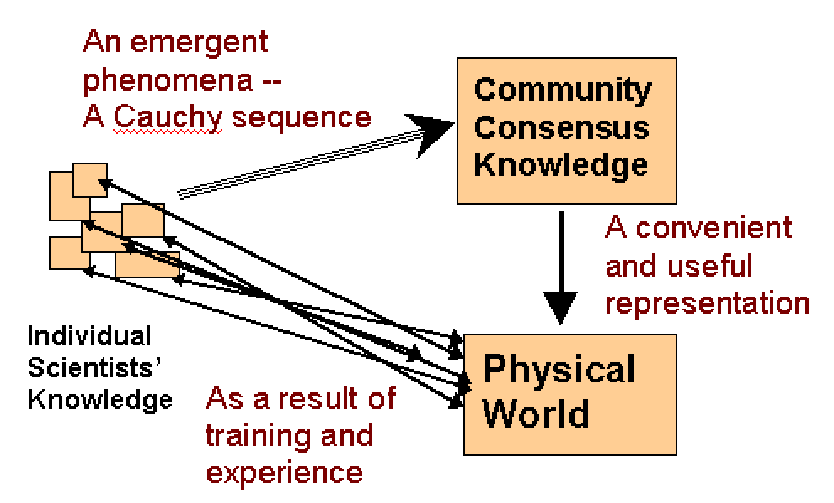
If no one individual has the complete map, why do I believe one exists? Real maps are constructed in a manner similar to the way we construct science. They are built by many surveyors. No one surveyor has made all the measurements that lead to a map of the US, for example. Furthermore, each atlas differs in some detail from each other atlas, yet we have little doubt that a true atlas could exist (though it would, of course have to be dynamic and limited to a preset resolution).[7] In mathematics, if we have a series of functions that get closer and closer to each other in a prescribed way then we say the sequence has the Cauchy property.[8] Even if we can’t find the true limit analytically, we find it convenient to act as if such a limit exists.[9] The natural mathematical structures of sets of functions behave much more nicely if we add the sets of Cauchy sequences to our space. It’s like adding the real numbers that fall in between the rationals. We can never calculate them exactly, but it would be very hard to describe the phenomenon of motion if we left them out.
In many areas of physics the sequence has converged — for all practical purposes. The community consensus on such items as classical mechanics of the planets of the solar system or the thermodynamics of weakly interacting gases, for example, is exceedingly strong — in part because we know the resolution that is relevant to most problems in these subjects. Just as we don’t need (i.e., find it useful to have) a map of New York which specifies the cracks in the sidewalk, we don't need to calculate the location of a satellite to nanometer accuracy.
If what we learn about physics education is to lead to a stable and growing community map, the community needs to document what we know and present conjectures and hypotheses for criticisms and questioning. This is particularly important in education.[10]
Human behavior in all realms is beset by wishful thinking – the tendency of people to really believe that what they want to be true is true. To some extent, the most important part of that process by which science builds its community consensus knowledge base is the part that probes and purges the wishful thinking of the individual scientist. Some parts of the process critical for this task include:
When it comes to education, wishful thinking is not just present, it is widespread and can take a variety of forms.
I have personally heard each of these responses from physics colleagues whose science and whose teaching efforts I respect.
If we want to understand what is happening in our classrooms, we have to understand our students well enough to understand the process they go through when they learn something. Learning is a complex process. Ever since Plato,[13] teachers have been developing principles of effective teaching and learning based on insights into human behavior. Psychologists only began to bring scientific tools to bear on the problem of human learning in the nineteenth century.[14] For much of the time since then, the community of psychologists got itself trapped in a number of dead ends. Freudians and behaviorists made the mistake of taking a few good insights and trying to build universal theories from them. One of the lessons we learn from the history of physics is that it rarely pays to let your theory run far ahead of your careful experiments.
During the twentieth century, psychologists and educators have made a number of fundamental steps that are beginning to form the core of a community map to help us understand how people learn and how they can be educated most effectively.
The Swiss psychologist Jean Piaget made a major advance in the science of learning in the first half of the twentieth century. He began with careful observations of his own children learning to make sense of the world around them and went on to produce many volumes of experimental observations on the learning and reasoning of children and young adults. The heart of what Piaget learned [15] is that the mind processes sensory data to create the coherent worldview we take for granted.[16] From this process comes the ideas of objects, classifications, and more complex patterns of association. Although the theories Piaget created have been substantially modified, much of what he learned remains valid, and much of what has been learned relevant to education since then, builds on his work. These principles are referred to as constructivism. A second important idea was developed by followers of the Russian psychologist Lev Vygotsky both in psychology and in education. They pointed out the important role of social interactions in the learning process. This work has had a profound impact on modern theories of teaching and learning.[17]
In the past half century there has been an impressive growth in the understanding of cognitive processes at all levels. Today, modern tools (many of them created by physicists) permit neuroscientists to offer glimpses of a complete reductionist structure underlying the processes of cognition.[18] But detailed studies of the neural paths by which a cat processes a visual signal are micro-variables ¾ too detailed and specific for us to use in solving the practical problems of education. We need some collective variables. It is likely to be a long time before a fully reductionist description of cognition is available — and even if one were, we would still want descriptions of students and classrooms in terms that are useful for designing effective lessons.
In the past few decades, educational researchers have begun to understand much about what is happening in the physics classroom. This knowledge fits well with what is known from cognitive science and allows us to begin to identify some elements of an emerging community map.[19]
I have selected five general principles from what psychologists and educators have learned. These can serve as the framework for our community map and help us to make sense of what happens in the physics classroom.
The first three of these principles are associated with the idea of constructivism and how it is implemented. Principles 1-4 are discussed in detail in my brief summary of cognitive science that appeared in this journal a few years ago.[20] The fifth principle summarizes the important work on group learning coming from Vygotsky and his followers.
The social learning principle is particularly important for physicists to keep in mind. Physicists as a group are highly unusual in many ways. They are in the extreme tails of distributions for curiosity, intellectual independence, and mathematical skills. They also tend to be highly self-sufficient learners. I once heard David Halliday, author of a famous textbook,[21] remark that what he enjoyed most as a student was sitting down by himself alone in a quiet room with a physics text and going one-on-one with the authors of the book — trying to understand them and figure out what they were trying to say. Many of us have similar inclinations. Physicists as a group seem to be selected for being able to learn on their own. But in examining my personal experiences of this type, I have decided that my learning on my own involves an ability to create an "internalized other" — to take a variety of viewpoints and to argue an intellectual issue with myself. This does not appear to be a commonly found characteristic and cannot be assumed in a general population of students.
The principles of our first draft of a community map for physics education are different in character from the laws we would write down for a community map of the physical world. They are much less like mathematical theorems and much more like heuristics. This is not a surprise, since the phenomena we are discussing are more complex and at a much earlier stage of development.[22] Indeed, some items are still controversial. Two facts in particular have caused some confusion.
The fact that science does not produce a perfect map has led some to claim that because science is not perfect, it is not truly objective. This concern of some postmodernists in a variety of fields is akin to that of the philosophers who were confused by Zeno’s paradox.[23] We need be no more concerned about this lack of perfection in science than we are about the fact that we can never know the number p or the function sin x perfectly. In a very real sense, neither p nor sin x exists.[24] We can, however, know them as accurately as we need. Of course the shadow that falls between mathematics and perfect knowledge is much slimmer than the one that falls between physics and perfect knowledge.
For example, there is a fundamental failure of consistency of classical mechanics produced by the need for radiation reaction. The presence of a third derivative of position in our equation of motion implies that we should be able to set the acceleration arbitrarily and undermines our interpretation of Newton’s second law.[25] But the parameters involved indicate that if we can’t treat radiation reaction perturbatively, then the situation usually requires a quantum treatment of the electron’s motion. So we don’t worry about it because we know classical mechanics can be thought of as an approximation. The value of classical mechanics today is similar to that of thermodynamics as described by Einstein. It will "never be proved wrong." We know its limitations and the systems in which it can be applied.
The fact that each individual constructs science (and everything else) for him or herself means that the teacher and the teacher’s teacher have gone through the same process that the student is going through. This has led a few educators to focus primarily on the student’s experience in exploring and creating ideas without consideration of the correctness of these ideas. This loses sight of two fundamental points: that we are trying to educate/acculturate our students, not just raise their self-esteem, and that science represents the knowledge of a community, not of an individual.[26]
In education as well as in science, our choices are not restricted to having a perfect community map or rejecting the idea of a map. The fact that many people misuse and misinterpret Piaget’s great discovery does not make it any less useful when carefully applied. Piaget and his followers have shown us that people take their sensory inputs and interpret them based on cognitive structures that have already been set up. Does this mean all knowledge is necessarily approximate? Does it imply that our theory of knowledge is self-referential? OK, we can handle that. As physicists, our community has struggled with both of these conditions in other contexts. Zeno’s paradox troubles us no longer and we are perfectly comfortable taking limits to get derivatives. The theory of motion is well understood and of immense practical use. As for self-referential systems, it’s well known to readers of this journal that quantum mechanics is self-referential in a most confusing way.[27]
When it comes to quantum mechanics, our community has chosen to cut the Gordian knot of self-referential measurement difficulties. Despite much public discussion and many statements that the Copenhagen interpretation is generally accepted, in practice the situation is more subtle. Most quantum physicists do not spend a lot of time worrying about measurement theory. It’s clear that the issue is complicated and various mechanisms can be imagined that might produce our apparently classical macroscopic world even though the underlying dynamics are fundamentally quantum mechanical.[28] I expect that the construction of macroscopic quantum states now being accomplished with lasers and superconducting systems will eventually lead us to a much better understanding of what the real nature of quantum peculiarities are (and that there are bound to be some very interesting and exciting surprises). I am delighted that a small fraction of our community is engaged in vigorously probing these issues. I am even more delighted that the difficulty has not prevented the rest of us from getting on with the business of understanding and using quantum mechanics in a practical (if incomplete) fashion.
I propose that we treat the idea of constructivism in the same manner. We consider the principles stated above as working hypotheses to be refined and tested by observation and experiment. When it’s possible, we avoid those areas in which their application would be debilitating. When it’s not, we rely on our experience and common sense. I refer to this approach as scientific constructivism.[29]
Even when they accept the importance of acculturating students to the community map of science, a few in the education community have pushed the community map of education to the extreme of "pure discovery learning." In this model, the teacher is not supposed to get in the way of the students’ creativity by helping them. The emphasis tends to be on learning the process of science rather than the content. Although the process of science is clearly important for students to learn, many of us find this approach highly frustrating and inefficient for teaching students at the college level. It takes a long time to get students to construct correct scientific ideas, even with the most carefully crafted environments. A pure discovery approach may be appropriate for some students, but it cannot be considered appropriate for the teaching of scientists, engineers, or technologists, who must master a large body of material.
Scientific constructivism allows us to go beyond the false dichotomy "constructivism vs. content." A scientific constructivist might ask the question: Given the goal of understanding a particular set of content material, what is the best way to create an environment in which the largest fraction of students possible attain that goal within a specified time frame?
Lillian McDermott, her collaborators, and her followers have created discovery learning approaches which include rather "tight" guidance. These approaches combine scientific constructivist assumptions with the need to "cover" substantial blocks of material for teaching scientists and engineers at the college level. It gives us an example of the fact that while pure discovery learning may be of limited value for the teaching of scientists, strongly guided discovery can work extremely well. It can both reach large fractions of our students and be more efficient than the traditional approach.
Traditional lecture-based instruction demonstrates that a reasonably good understanding of science can be taught to a select 5% of the population. Applications of pure discovery learning show that students weak in math can be led to discover for themselves the simplest tools and principles of science. Research using McDermott’s Physics by Inquiry[30] and Tutorials in Introductory Physics[31] (and the work of Laws,[32] Thornton, and Sokoloff [33] which adapts and follows her model) shows that a large fraction of students can be helped to build a robust and functional understanding of many complex topics.
In one example, McDermott and her group have shown that with three hours of carefully guided instruction in a recitation-like small-group environment facilitated by graduate assistants, 85% of the students in a calculus-based physics class can be taught to construct the pattern of light produced on a screen by any combination of bulbs and any shaped mask. The success rate of traditional instruction with the same students is 25%.[34] The work of Thacker et al. demonstrates that using McDermott’s methods, pre-service elementary school teachers can learn to analyze the qualitative behavior of complex circuits more effectively than honors physics majors in traditional instruction.[35] Many more examples exist in the published literature. (See the article cited in ref. 19.)
A critical element in building a community map for education is the application of the two fundamental tools of science, observation and analysis. Educational phenomena permit us to carry out observations in controlled experiments, but experiments in physics education differ in a number of respects from the idealization of a traditional physics experiment. Among the differences are:
Note that I have referred to our idealization of a traditional physics experiment. In practice, our real experiments rarely fit this mode. The difficulties with doing careful educational experiments all have their analog in traditional physics research.
Classrooms, students, and teachers are all complex systems. Experiments with such systems involve many variables, some of which are unknown. It is difficult to determine the effect of past experience and cultural environment on students and teachers. The formal education of students prior to their enrollment in undergraduate courses may significantly affect how they interpret what is taught. As is sometimes the case in traditional physics research, it is almost impossible to identify all the relevant variables or to perform a truly controlled experiment in which only a single variable is changed — sometimes it is even impossible in principle. For example, quantum experiments are not repeatable at the level of an individual event. Although we assume that all electrons, unlike people, are identical, it is still not possible to control an experiment so that each electron behaves in exactly the same way. In the cases of electrons and people, only the behavior of populations can be predicted reliably. Furthermore, we are not free to perform arbitrary experiments on our students. Ethical considerations also create serious constraints.[36] Experience demonstrates, however, that reliable and reproducible educational results can be obtained that are extremely useful for the development of effective instruction. (An example is given below.)
In an idealized physics experiment, an effort is made to ensure that the effect of a probe on the system that is being measured is small. However, it is not always possible to find such a probe, especially in strongly interacting systems. If I want to probe the character of some of the excited states of a nucleus, I may have to use a probe that interacts strongly to excite those states (e.g., a nucleon or meson). These probes, however, may interact more strongly with the nucleus on the way in and on the way out than when they excite the state to be studied. This strong interaction can lead to uncertainties and ambiguities in how the information about the nucleus is extracted. On the other hand, weak coupling is not always even desirable in physics education research. For example, to be able to infer what is really going on in the minds of students, the investigator often must interact strongly with them — talking to them directly and asking them many questions.
The level of quantification must be appropriate to the situation that is being studied. In traditional physics experiments, the goal is to obtain quantitative results with the uncertainty in the measurements well-specified and as small as possible. However, meaningful quantitative results cannot be achieved unless one has a sound qualitative understanding of the physics involved. In studies involving students, the value of quantitative results also depends on our understanding of qualitative issues, which usually are much less well understood than in the case of physical systems. To be able to determine the depth of students' knowledge and the nature of their difficulties, it is necessary to probe the reasoning that lies behind their answers. The analysis of numerical data alone may lead to incorrect interpretations. Detailed investigations with a small number of students can be very useful for identifying conceptual or reasoning difficulties that might be missed in large-scale testing. On the other hand, if the population involved is too limited, the results may be idiosyncratic and important information may be missed.
An additional issue about educational experiments that appears on the surface different from our experience in physics is the issue that is referred to pejoratively by some social scientists as mentalism. In our goal of understanding what is going on in education, many educational researchers (myself included) attempt to infer what is happening in the mind of the student. The objectors complain that one can never really know what is really happening inside someone’s mind by direct observation so one should not talk about it. I have even heard these objections from some physicists. I find this quite strange, since in physics we have for nearly a century made immense progress by talking about objects whose existence we only infer from complex indirect observations. This began with Maxwell’s inferences on the size of molecules, continued to Rutherford’s inference of the existence of an atomic nucleus from scattering phenomena, and reached a peak with the discovery of quarks — which many physicists believe can never be isolated. Nonetheless, we find it extremely useful to talk in terms of these "non-observable" objects and we would find it extremely difficult to do contemporary physics without them. As we learn in physics, inferring the existence of structures that are not directly observable is an essential element in building an understanding that works. In order to make sense of what is happening when a student thinks about a physics problem, we have to hypothesize structures and processes that are dimly hinted at in demonstration interviews[37] or think-aloud protocols.[38]
The education research that is building a community map of education can give important new insights that help instructors understand what is going on in a physics class. I will give four examples that demonstrate the possibility of learning valuable information from education experiments and that demonstrate the value of developing curriculum based on scientific constructivist principles.
My first example demonstrates that listening carefully to one student in a detailed interview can have surprising results that can help substantially in understanding what is going on in a class.
As part of a project to develop instructional materials for the subject of mechanical waves, Jeff Saul, Michael Wittmann, and I gave my engineering physics students the quiz problem shown in Fig. 2.
Consider a pulse propagating along a long taut string in the +x-direction.
The diagram below shows the shape of the pulse at t = 0 sec. Suppose the displacement of the string at this time at various values of x is given by
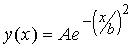
 B. For the instant of time that you have sketched, find the displacement of the string as a function of x. Explain how you determined your answer. |
We were not surprised to find that many could not write the correct equation, but we were surprised to find that a significant fraction of students drew the pulse as shrinking substantially in size. I had not discussed the damping of waves on a string in lecture, and, although in principle the answer is correct, it seemed a bit too sophisticated for the level at which we thought the class was functioning. The situation became much clearer when Saul and Wittmann carried out a few detailed interviews, asking the students to consider the problem and explain their reasoning. One student (a high achiever who eventually earned an A) responded as follows:
Okay. Over a long, taut spring, the friction or the loss of energy should not be significant; so the wave should be pretty much the exact same height, distance -- everything. So, it should be about the same wave.
No, wait. Okay... ‘the displacement of [READING] ... is given by’...looking at the function of y ... Let's see...I guess it'll be a lot smaller than the wave I drew, because the first time -- x is zero, because e raised to the zero's going to be 1.... And then as x increases, ... e raised to the negative... So, if x keeps on getting bigger, e raised to the negative of that is going to keep on getting smaller. So the -- So the actual function's going to be a lot smaller.
The student began with the view we expected — that the pulse would just continue without significant reduction in size. But the presence of the equation in the problem triggered an association that made him question his interpretation. He was confused about how to read and interpret a function [39] and had particular trouble handling the difficult problem of re-interpreting a one-variable function as a restriction of a two-variable one. Once we understood this, we were able to interpret the results of the quiz, document that this was happening to many students despite my careful efforts in lecture to be perfectly clear, and develop curricular materials (a guided-discovery group-learning tutorial) that successfully dealt with the issue.[40] Focusing on understanding how a small number of students constructed their responses to our question helped us unravel the instructional problem.
A second example shows that there are surprises when one carefully probes a class’s understanding. It also illustrates the difference between the impact of having outstanding and insightful teachers share their experiences, and detailed research in building a community-consensus knowledge base.
When Arnold Arons’ book on teaching physics [41] first appeared in 1990 I was absolutely delighted. Although I was not yet a physics education researcher, I had had a strong interest in physics teaching for many years. I had read many of Aron’s papers and had great respect for them. I read the book cover to cover and annotated it heavily. In chapter 6 (p. 152) you will find the sentence: "...This paves the way for eliminating misconceptions such as repulsion between a north magnet pole and a positive electric charge, and so on." I wasn’t very worried about this. It isn’t even underlined in my copy of Arons. (I underlined about a fifth of the sentences in that chapter.)
But in January of 1994, the Physics Education Group (PEG) at the University of Washington reported the results of a study of engineering students' responses to being taught about magnets.[42] Traditionally, many teachers and textbook writers assume, just as I did, that students know little about the subject, so a good way to introduce it is by analogy with electric charge, the topic typically presented just before magnetism. The Washington PEG demonstrated that before the lectures on magnetism, more than 80% of their engineering students confused electric charges and magnetic poles as measured by the simple problem shown in Fig. 3. After traditional instruction, this number remained above 50%. I was both flabbergasted and distressed at hearing this. I had taught the subject off and on for nearly 25 years and was teaching it at the time of the presentation. I furthermore believed that I listen carefully to students, and I was already sensitized to the issue that students bring in previous knowledge. Yet I had never imagined such a confusion was common. I probed my class upon my return and, needless to say, found exactly the same results as the Washington group.
| A bar magnet is hung from a string through its center. A charged rod is slowly brought up as shown. In what direction will the magnet tend to rotate? (The magnet will not rotate since electric charges and magnetic poles do not exert static forces on one another.) |

|
Now the Arons book is still one of the best "teacher-to-teacher" books available. Arons shares the insights and tricks he has learned from his extensive and insightful experience with students over many decades.[43] Despite my respect for Arons’ insights, I was skeptical about the importance of a possible student confusion between electric charge and magnetic poles. Indeed, I felt my personal experience contradicted it. The point was only convincingly brought home to me by the solid experimental data offered by the UW PEG.[44]
In order for educational experiments to be useful in building a community map, they need to generalize from the test population to a broader group. Our previous examples hinted at the generalizability of narrow studies. In the first example I was able to extend our interview results on waves from a small number of students to my whole class. In the second example, the McDermott charge/magnet results extended from the University of Washington to my own class at Maryland. But I became firmly convinced of the robustness of some education research as the result of an experience I had when teaching engineering physics in the early ‘90s.
In 1991 I taught the engineering physics class for the first time. (I had frequently taught a smaller class for physics majors and the large algebra-based introductory class.) Before beginning the class, I read Thornton and Sokoloff’s paper in which they claimed that traditional lectures failed to help students learn to interpret the concept of instantaneous velocity.[45] The students of traditional lecturers in six colleges and universities with a variety of teaching styles did rather poorly on a simple question that asked them to match the description of a one-dimensional motion with a velocity graph. The problem is given in Fig. 4. Thornton and Sokoloff also claimed that two two-hour laboratories designed using constructivist principles solved the difficulty for most students. In these labs, students used sonic rangers and microcomputer data acquisition to display position and velocity graphs of their own motions. Guiding questions required that the students make predictions as to what the graphs would look like, carry out the experiments, and reflect on their own thinking.
| An object's motion is restricted to one dimension along the + distance axis. Select the velocity graph that is the best choice to describe each answer. You may use a graph more than once or not at all. Which graph shows (a) an object going away from the origin at a steady velocity? (b) an object moving toward the origin at a steady velocity? (c) an object standing still? (d) an object changing direction? (e)an object that is steadily increasing its speed? |
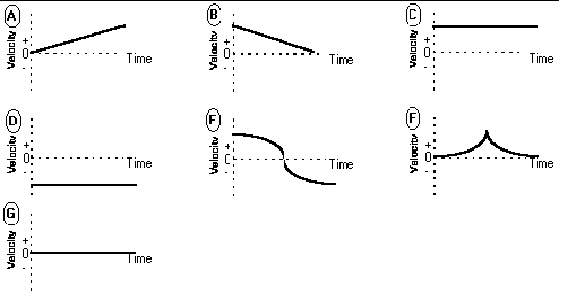
Fig. 4: Problem from Thornton and Sokoloff that reveals student difficulties with the concept of velocity.
I was skeptical of this result for two reasons. First, I was sure that I could teach the subject in lecture. After all, it wasn’t very difficult, and I had great confidence in my ability to make things clear. Second, I felt that four extra hours of instruction gave the students with lab too much of an advantage. I thought I would try it myself.
When we came to the topic of velocity, I prepared 2˝ hours of lecture on the subject. Although it was a large class (about 175 students), I tried to make sure most of the students were mentally engaged. I wrote clear definitions on the board and walked a pattern and made them graph it in their notebooks. I gave examples that were realistic and related to their experience. I used our high quality demonstration equipment — including the equipment Thornton and Sokoloff used in their labs. And then I gave their problem on my mid-semester exam.
The results were both humbling and elating. Despite my best efforts in lectures, the results my students obtained were very close the 6-school average Thornton and Sokoloff reported from lectures at other universities. (My results are given as the first and second bars for each question in Fig. 5. Note that error rate is reported rather than the success rate.) On the other hand I was very pleased with the robustness of the result. I had expected to do better, but failing that, I had at least expected some large fluctuations as a result of the different emphasis between my lectures and those of other faculty. This was exhilarating — like when in my freshman lab I measured g with a long pendulum and got the answer in the textbook.
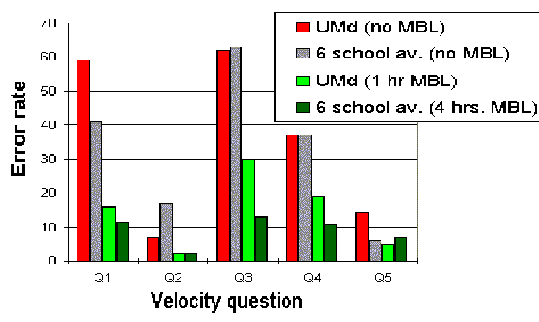
5: Error rates on the problem shown in figure 4.
The next time I taught the course was two years later. I had just completed a sabbatical with Lillian McDermott’s group at the University of Washington, had learned her guided-discovery model, and was trying a first implementation of a set of tutorials they had developed. I decided to replace her velocity tutorial by one that drew on Thornton and Sokoloff’s constructivist labs. So instead of 2˝ hours of lecture and one hour of recitation, I gave my students one hour of lecture and one hour of MBL tutorial. The result was a striking improvement over my best lecture efforts (the 3rd bar in each question) even if it wasn’t as good as four hours of lab (the 4th bar).
These results not only demonstrate the repeatability of the Thornton and Sokoloff measurements, they demonstrate the effectiveness of their technique in a reasonably well-controlled experiment.
The first three examples (and many others to be found in the research literature) demonstrate that researching students’ real difficulties and designing learning environments to deal with those difficulties can be quite effective in helping students learn specific concepts. But what about more broadly? Can the principles of scientific constructivism and the fledgling elements of our common educational map help us create effective curricula? How could we begin to tell if these curricula improve on traditional instruction?
As part of his dissertation research,[46] Jeff Saul compared student learning of mechanics in traditional (lecture + recitation) first-semester calculus-based physics with three constructivist curricula. In two of them, McDermott’s Tutorials and Heller’s Group Problem Solving (GPS), the recitation is replaced by a group-learning activity (one hour per week). In one, Laws’s Workshop Physics, lecture, lab, and recitation are combined into three two-hour guided-discovery lab sessions per week. All three of these curricula rely heavily on the growing community-consensus knowledge base in physics education.
Saul evaluated implementations of these curricula at 14 colleges and universities. He collected data from a total of 14 different classes with more than 3000 students. Many kinds of data were collected, including the results of open-ended exam questions, problem interviews, attitude surveys, and a conceptual survey. Due to space limitations I will only discuss the last of these here.
One of the tools Saul used in his evaluation of student learning was the Force Concept Inventory (FCI).[47] This is a 29-item multiple-choice test carefully designed on the basis of student interviews and published research to probe student understandings of the basic concepts of Newtonian dynamics. The questions are qualitative, are mostly phrased in common speech rather than as abstract physics problems, and have distractors based on the most common student errors. Faculty looking at this test tend to significantly overestimate their students’ success on this test after instruction.
Studies of many classes by Hake [48] suggest that an appropriate figure of merit for success on this test is the fraction of the possible gain obtained. We write this as
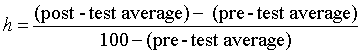
In Saul’s study, he confirmed Hake’s result that traditional classes average about a 20% value for h.[49] The constructivist reform curricula do significantly better. The curricula that modify only one hour of instruction (Tutorials and GPS) averaged 37%, while the curriculum that completely replaces lecture with guided-discovery instruction (Workshop Physics) averaged 43%.[50] I have displayed these results in a somewhat idealized form for easier interpretation by fitting the distributions for each method with a two-parameter (mean and width) normalized Gaussian. These are displayed in Fig. 6.
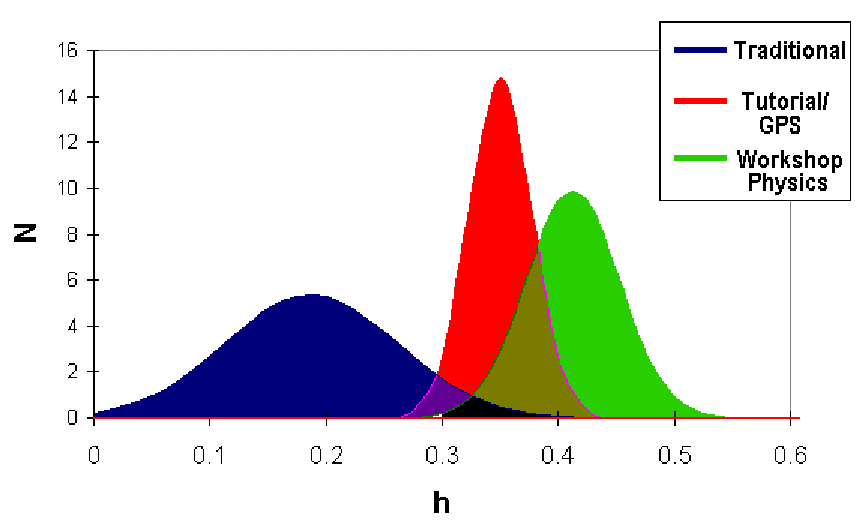
Fig. 6: Gaussian fit to histogram of FCI gains in traditional, tutorial, group problem solving (GPS), and workshop physics classes at 8 institutions.
Saul confirmed the FCI results by more detailed observations of student responses to open-ended exam questions and by interviews. These results demonstrate that curricula developed based on the community map in physics education can produce substantial improvements in the average student’s concept learning. Most of the institutions tested were secondary implementers of the curricula, not developers. This demonstrates that there is significant transferability of the curricula tested.
If we grant that physics education is beginning to use the culture of science to create a community-consensus knowledge base for physics education, a critical question still remains. If physics education research is to build a community-consensus knowledge base, what community should build it? Although there is much that is valuable that has been created by cognitive scientists and education specialists, I argue that if physics education research is to make significant progress in understanding university level physics education it must involve physicists and physics departments. The community building the community map must include the community of those who actually teach physics — the physicists.
Granted that physics education research is interdisciplinary and applied, is there a reason why it is useful to do it in a physics department? Surely it could be done equally well in an education school, relieving physicists of the need to worry about such issues? In principle, the answer could be yes. In practice, there are strong reasons that physics education research needs to be done in physics departments — at least in part. There are three reasons for this: access, benefits, and competition.
First, education researchers need good access to physics courses and physics students. Research exam questions must appear on real examinations and new curricula must be tested with real physics students. This is possible if a researcher in an education school has good relations with a physics department and is well aware of the many pressures, political constraints, and psychological issues involved in the development and delivery of every physics course. But it is often difficult enough for an insider to develop the access needed from his or her colleagues. Being from another department or even another college raises the bar. Second, the primary benefits of physics education research, improved learning, increased satisfaction, and sometimes even increased enrollments, accrue to the physics department directly. Getting one department in the university to spend their resources to benefit another department can be difficult. Third, there is significant competition for the limited resources of education schools. College level physics education is a small part of their mandate. Other issues, such as K-12 education and topics such as learning reading and arithmetic, are just as important as university-level physics education and affect much larger audiences.
But there is a deeper reason for physicists to be involved in physics education research beyond the cultural and political. Much of what needs to be done in physics education research is very similar in spirit to activities commonly considered to be the purview of physicists.
Is it physics?
The four examples of research I described above were done by physicists acting as education researchers and curriculum developers within physics departments, studying the learning of university students. This kind of research effort is growing. As of this writing, there are more than a dozen research physics departments that have programs in physics education research. But shouldn’t education research only be done in an education school rather than a physics department? After all, it isn’t physics, is it?
In order to consider the question: "Is it physics?" let me begin with my subjective response and then analyze that response. In the 30 years since I received my Ph.D. in nuclear physics I’ve seen and done a lot of different kinds of physics. I’ve worked on phenomenology and the development of abstract mathematical theories. Though I’m a dyed-in-the-wool theorist, I’ve consulted with experimentalists and discussed new data and the plan of experiments. I’ve served on national committees evaluating proposed research projects and served as chair of a Department that had funded research programs in 14 different areas. I’ve seen the growth of space physics and biophysics and watched the decline and rebirth of university-based atomic and solid state physics. The research I’m now doing on physics education still feels like physics to me.
But then why do I get so much hassle from a few colleagues whose first reaction is that I should move to the College of Education? (Most of my colleagues appear quite happy to have me remain in the Physics Department.) I conjecture that there are two important reasons. First, because their imagined picture of what I and my students do, constructed on the basis of their own experience with education schools or newspaper reports of what has been learned from research in education, is very different from what we actually do. Second, because they orient so strongly on creating an accurate map (refer to Fig. 1) that they sometimes forget the role of the mind in doing physics.
Discovering new physics is like finding new territories to add to our map. But physicists, even those whose primary goal is to discover new territory, do other things than cover new ground. Physics is really about building mental maps that allow us to make sense of the world. To do this we have to create map structures that match not just what happens in the physical world but the ways we can comfortably think about it. Many great advances in physics have arisen from folks who rethought things they already knew in a different way. We’re not just creating the map — we’re optimizing it.
In his recent book, How Nature Works, Per Bak [51] states "The laws of physics are quite simple. They are expressed in mathematical equations that can all be written down on a couple of notebook pages. However, the mathematics involved in solving these equations, even for simple situations, can be quite complicated." This makes the point Bak is trying to make, since his book focuses on the emergence of complex phenomena from simple equations, and it is a statement that I think many physicists would agree with. But we tend to forget that some of the "simple" equations may have required years of training for us to be able to interpret. The equations of physics are not just mathematical equations. Their interpretation requires building a substantial collection of spontaneous cognitive constructions (i.e, learning). The equations
![]()
appear quite simple. Indeed, they only involve 6 symbols — fewer than many equations seen in a freshman physics class. But even many professional physicists will not recognize Maxwell’s equations expressed using differential forms and may well require weeks of additional education before they can learn to disentangle the familiar electric and magnetic fields and their sources from this highly condensed notation.
A whole range of great advances including Newton’s invention of the calculus, Hamilton’s reformulation of Newton’s laws, Gibbs’s vector notation, and Feynman’s sum over histories, could be brushed off as merely rethinking what was already known in other forms. Yet it can convincingly be argued that each of these great reformulations played major roles in facilitating substantial advances and the creation of new physics.
In order to do the best physics education research, we not only have to create an understanding of how people think, thereby possibly creating new cognitive science, we have to rethink / reformulate the physics in order to understand cognitive elements we take for granted but which our students lack.
At this point, physics education research is a highly applied field focusing largely on our most important problem: teaching introductory physics to non-physicists. We spend a lot of time redesigning our map, optimizing it for students who don’t possess our training or experience. We don’t yet have reformulations of our way of thinking about physics that lead to new physics, and it may be a long while before we get one. But I consistently find that the rethinking of the physics I am researching leads me to new and better understandings of physics that I have learned and taught many times. One example of this is David Hestenes’s analysis of the basic ideas of Newtonian mechanics in conjunction with his study of student difficulties.[52] Observation of persistent student confusions leads to the emphasis of the importance of what I refer to as Newton’s 0th Law of Motion:
At a time t, an object responds only to forces that are exerted on it itself at the time t.
This seems almost trivial ¾ unnecessary to fuss about, until one observes students "transferring" forces from connected chains of objects (sometimes correctly, sometimes not), or insisting on including the forces the object exerts in its free-body diagram, or describing a thrown ball as "using up the force that was given to it as it rises."
In order to understand what is happening in our physics classes, deep rethinkings of the physics we teach are essential, but cannot be done entirely within our own heads. As physicists, we have been educated to the point that our spontaneous reactions to a word, phrase, equation, or physical situation can be substantially different from that of almost all of our students — especially at the introductory level. Figuring out our tacit (and often unnoticed) assumptions requires both doing physics and understanding the cognitive psychology of understanding physics. These essential elements make physics education research a true interdisciplinary part of physics.
Barriers to creating the consensus: Education is not just local
With the more detailed perspective provided by the above discussion, let’s return to the questions posed at the beginning of this article. Why do we never seem to share and pass down to succeeding generations anything we learn in physics education? Can we do anything to change this?
I believe the answer is clear. The problem is that many physics departments believe they have to create their own solutions. Worse yet, within a single department, each individual physics instructor often wants to have complete freedom in constructing and delivering his or her own class. Sharing of experiences and insights is rare even among faculty teaching the same course in succeeding years, especially at research universities. Treating education as a problem to be handled individually rather than scientifically by the community at large, instead of creating a community-consensus knowledge base, we continue to (in the felicitous phrase of Arnold Arons) "reinvent the flat tire." In Fig. 1, instead of having a tightly interacting community to purge wishful thinking and build an accurate and robust community map, we have a loose group of weakly interacting individuals. No consensus emerges and the series fails to converge. We individually think we know some things, but until we get into the habit of testing that knowledge, finding out and evaluating what other people know, and in general asking "How do we know this and why do we believe it?" we will not be able to cumulate and progress. The missing element in building a robust knowledge base for physics education is the process and culture of science. The growing community of physics education researchers, both in physics departments and in education schools, who are applying the process of science to the problem and the growing interest in physics education research are important steps in remedying this situation.
If we want to improve the way that we deliver physics education in colleges and universities we have to face the issue ourselves. We cannot rely on someone else to do it for us. Education research on university level physics is an interdisciplinary activity. It can be done successfully in a variety of ways, but it always requires a connection with a physics department and the commitment of a physics department to engage in, participate in, and take seriously the results of education research.
1. R. A. Millikan, Mechanics Molecular Physics and Heat (Ginn and Co., Boston MA, 1903), p. 3.
2. P. Laws, "Millikan Lecture 1996: Promoting active learning based on physics education research in introductory physics courses," Am. J. Phys. 65: 1, 14-21 (1996).
3. R. A. Millikan, The Electron, Its Isolation and Measurement and the Determination of Some of its Properties (The University of Chicago Press, Chicago IL, 1917).
4. There is a more subtle interpretation to the Phillips quote. Even if we have solved a physics education problem, because physics education depends on the experiences of both students and teachers, the problems are a (fortunately slowly) moving target.
5. L. Carroll, Sylvie and Bruno (Garland Pub., New York NY,1976) p. 265.
6. Mathematically, this is even true of a sphere, which cannot be mapped by a single non-singular map to a Euclidean plane. See for example H. Flanders, Differential forms, with applications to the physical sciences (Academic Press, New York NY, 1963).
7. Though note that a more accurate map is not necessarily more useful. A map constructed from aerial photographs can be very difficult to read. A map is more useful if it is constructed with an appropriate level of abstraction. Those New Yorkers "of a certain age," will recall the old subway maps — imbedded on a realistic map of the city with correct relative distances. The current subway maps are more symbolic, emphasizing the different lines and their topological relationships rather than accurately represented distances.
8. If you take two functions from far enough out in the sequence they will be as close together everywhere as you want. (Given any e greater than 0 there is an N such that if m,n > N, |fn(x) – fm(x)| < e for all x.)
9. This is called completing a Hilbert space. See for example, M. Reed and B. Simon, Methods of Mathematical Physics: Functional Analysis (Academic Press, New York NY, 1980) p. 7.
10. Other goals are possible, such as helping an individual teacher understand the effectiveness of a particular educational innovation in her own classroom.
11. We try to make experiments as similar as possible, but it is not, of course, possible to ever reproduce an experiment exactly – even if the identical apparatus is used. These small variations help us understand what variables are important (e.g., the colored stripes on the resistors) and which are not (e.g., the color of the insulation on the wires). 12. Note from this example that wishful thinking does not necessarily imply a rosy view of a situation. It may be that the wishful thinking is that "the situation is so bad that there is nothing I can do about it and therefore I don't have to make an effort." 13. Plato, "Meno," in The Dialogues of Plato, Volume One, B. Jowett, transl. (Random House, New York NY, 1937) 349-380. 14. H. Gardner, The Mind's New Science: a history of the cognitive revolution (Basic Books, New York NY, 1987) 15. This idea in fact goes back to Descartes. What Piaget added was the empirical observations that document the result in detail. See for example the discussion of Descartes' work in S. Savage-Rumbaugh, et al., Apes, Language, and the Human Mind (Oxford U. Press, New York NY, 1998) p. 90.
16. A wonderful example of what happens when the brain doesn't work properly to create the idea of objects from visual images is given in the title case study in O. Sacks, The Man Who Mistook his Wife for a Hat (Pan Books, London ENG, 1985).
17. R. Van der Veer and J. Valsiner, The Vygotsky Reader (Blackwell, Oxford UK, 1994); D. W. Johnson, R. T. Johnson, and E. J. Holubec, Circles of Learning: Cooperation in the Classroom (Interaction Book Co., Edina MN, 1993).
18. P. S. Churchland and T. J. Sejnowski, The Computational Brain (MIT Press, Cambridge MA, 1992).
19. In addition to the work discussed below by physicists, I have found the work of many researchers in the education community to be of great value in understanding what is happening in my classes, in particular, John Clement, Andrea diSessa, David Hammer, Pat Heller, Peter Hewson, and Alan Schonfeld, among others,. For specific references to work on physics education by both physicists and educators see L. C. McDermott and E. F. Redish, "Resource Letter on Physics Education Research," Am. J. Phys., to be published.
20. E. F. Redish, "Implications of cognitive studies for teaching physics," Am. J. Phys. 62, 796-803 (1994).
21. D. Halliday and R. Resnick, Physics (John Wiley and Sons, Inc., New York NY, 1961).
22. Astronaut and astrophysicist Pinky Nelson has remarked: "Education is not rocket science — it's much harder." Shaping the Future Conference, University System of Maryland, College Park MD, Nov. 30, 1998.
23. Zeno's paradox is an old proof that motion is impossible. To reach any distance you must first go halfway. To cover the second half of the remaining distance you must go half the remaining way, etc. To go any distance you must therefore cover infinitely many distances. Since this is obviously (sic!) impossible in a finite time, you cannot cover any finite distance in a finite time, hence motion is impossible.
24. Except, in the case of the sine function, for a finite number of particular angles where the result can be calculated exactly. 25. P. Dirac, "Classical theory of radiating electrons," Proc. Roy Soc. (London) 167, 148-169 (1938).
26. An excellent discussion of these difficulties can be found in A. Cromer, Connected Knowledge (Oxford U. Press, 1997).
27. The problem occurs when a physical system we are supposed to be measuring permits a number of different results. If we describe the system of observer + apparatus + system to be measured by a quantum wavefunction, the time evolution of the state will lead to a wavefunction in which the system to be observed, the apparatus, and the observer all simultaneously coexist in states having different results. See for example, John Gribben, In Search of Schrödinger's Cat (Bantam Books, New York NY, 1985).
28. Some approaches that have been considered include the randomization of uncontrollable phases and the coherent build up of minuscule time-irreversible pieces of the Hamiltonian over macroscopic times leading to collapse of the wave packet, among others.
29. The use of constructivism in education has bifurcated into a wide variety of groups, with acrimonious arguments as to who are the "true" constructivists. Among this panoply of competing views there are some similar to those we describe here. See for example, D. I. Dykstra, Jr., C. F. Boyle, and I. A. Monarch, "Studying Conceptual Change in Learning Physics," Science Education 76:6, 615-652 (1992); von Glasersfeld, Ernst, "A Constructivist Approach to Teaching" in Constructivism in Education, L. P. Steffe and J. Gale (eds) (Lawrence Erlbaun Associates, Hillsdale, NJ, 1995) pp 3 - 16.
30. L. C. McDermott and the Physics Education Group at the University of Washington, Physics by Inquiry, Vols. I and II (John Wiley & Sons Inc., New York NY, 1996).
31. L. C. McDermott, P. S. Shaffer, and the Physics Education Group at the University of Washington, Tutorials in Introductory Physics (Prentice Hall, Upper Saddle River NJ, 1998).
32. P. Laws, Workshop Physics Activity Guide (John Wiley and Sons, Inc., New York NY, 1997).
33. R. Thornton and D. Sokoloff, Tools for Scientific Thinking (Vernier Software, Ortland OR, 1995); D. Sokoloff, P. Laws, and R. Thornton, RealTime Physics (John Wiley and Sons, Inc., New York NY, 1998).
34. K. Wosilait, P. R. L. Heron, P. S. Shaffer, and L. C. McDermott, "Development and assessment of a research-based tutorial on light and shadow," Am. J. Phys., to be published.
35. B. Thacker, E. Kim, K. Trefz and S. M. Lea, "Comparing problem solving performance of physics students in inquiry-based and traditional introductory physics courses," Am. J. Phys. 62, 627-633 (1994).
36. These are similar to constraints in medical research.
37. In a demonstration interview a student is shown a physical apparatus and asked to explain what they think will happen in a particular circumstance. Such interviews were used by Piaget and have become a crucial element in the observations of McDermott and her colleagues.
38. In a think-aloud protocol a student is presented a task (such as a physics problem to solve) and asked to "think out loud." See K. Ericsson and H. Simon, Protocol Analysis: Verbal Reports as Data (Revised Edition) (MIT Press: Cambridge MA, 1993).
39. This is a common problem even at the University level and is well known to math education researchers. See, for example S. Vinner, and T. Dreyfus, "Images and definitions for the concept of a function," Journal for Research in Mathematics Education, 20:4, 356-366 (1989).
40. Michael Wittmann, Making sense of how students come to an understanding of physics: An example from mechanical waves, Ph.D. Dissertation, University of Maryland, 1998.
41. A. Arons, A Guide to Introductory Physics Teaching (John Wiley and Sons, New York, NY, 1990).
42. P. A. Krause, P. S. Shaffer, and L. C. McDermott, "Using research on student understanding to guide curriculum development: An example from electricity and magnetism," AAPT Announcer 25, 77 (Dec., 1995).
43. Arons does include citations to education research, especially in the sections on mechanics, but the book focuses on raising issues and offering solutions, not documenting them.
44. Note further that this result had been known previously and even published, but not in a journal which I looked at regularly or which was conveniently available.. D. P. Maloney, "Charged poles," Physics Education 20, 310-316 (1985).
45. R.K. Thornton and D.R. Sokoloff, "Learning motion concepts using real-time microcomputer-based laboratory tools," Am. J. Phys. 58, 858-867 (1990).
46. J. M. Saul, Beyond Problem Solving, Evaluating Introductory Physics Courses Through the Hidden Curriculum, Ph.D. Dissertation, University of Maryland, 1998.
47. D. Hestenes, M. Wells and G. Swackhammer, "Force Concept Inventory," The Physics Teacher 30:3, 141-158 (1992).
48. R. R. Hake, "Interactive-engagement vs traditional methods: A six-thousand-student survey of mechanics test data for introductory physics courses," Am. J. Phys. 66, 64-74 (1998).
49. It was important to confirm this since Hake solicited results after the fact and those classes with poor results might have chosen not to report them.
50. The Workshop Physics classes tested were early secondary implementations. The well-established primary implementation at Dickinson College consistently scores well above this level.
51. P. Bak, How Nature Works (Springer Verlag, New York NY, 1996).
52. D. Hestenes, "Modeling games in the Newtonian world", Am. J. Phys. 60, 732-748 (1992).
| University of Maryland | Physics Department | PERG UMD |
|---|---|---|
 |
 |
 |