The University of Maryland offers a physics course as part of the Maryland collaborative for teachers' preparation [MCTP] project. One of the course aims is to promote the learning of the concept of a function through the learning of physics. The students learn in small groups, through problem solving and with the aid of microcomputer based laboratories. Students are asked to examine and find connections between experiments, stories, graphs and algebraic representations. Analysis of observations of students' group work in the course revealed that experiments differed from stories in many characteristics as graphs differed from algebraic expressions. Similarities were found among the translation process from an experiment or a graph to a story or an algebraic representation. Similarities were also found between the opposing direction translations. These translations differed in many characteristics from translations between graphs to experiments and from translations between algebraic equations to stories. According to the above analysis the four situations -- experiment, story, graphical and algebraic representations -- can be presented has vertexes of a parallelogram. Each edge and diagonal of the parallelogram represents a bi-directional arrow of possible translations. Between parallel edges there are many similarities.
The research reported in this paper was supported by the National Science Foundation under grant No. DUE-9255745. The opinions expressed in this paper do not necessarily reflect the views of the foundation. We would like to thank Dr. Richard Steinberg for his constructive comments on the theory presented in this paper.
Information on other research conducted in the MCTP can be obtained in the MCTP Web site: http://www.wam.umd.edu/~toh/MCTP.html.
The current reforms in mathematics and in science education call for making connections between mathematics and science, applying technology, and advocate learning by inquiry (National Council of Teachers of Mathematics [NCTM], 1989; American Association for the advancement of Science [AAAS], 1993; National Research Council [NRC], 1996). In the spirit of these reforms, the NSF funded project, "Maryland collaborative for teachers' preparation" [MCTP], prepares pre-service teachers to teach science and mathematics in grades 3-9. In their teaching they are expected to connect between the disciplines, and use technology. One goal is to have preservice teachers employing instructional strategies that are compatible with constructivism perspectives. For example, teaching through student centered problem solving in small groups, addressing conceptual change, and dealing with more fundamental principles and less memorization of facts.
The program of the MCTP project includes instruction that matches the goals. Believing that the preservice teachers may remodel their university instructors, special courses in science and mathematics were designed. Most of these courses were taught by faculty in an inquiry mode of instruction, utilizing an interdisciplinary approach and microcomputer based laboratory technology.
The research described below was set to examine the application of representations in an MCTP science course.
The goals for the course were to model the inquiry approach by creating a totally laboratory based course, by selecting a limited number of concepts, having the students work in small groups, and experience authentic assessments. Students also were expected to design experiments, carry them out, and present their results with evidence to support their conclusions. The course aimed to utilize science and mathematics in a seamless fashion, with students encouraged to work with science situations, and mathematical representations and to be able to make transformations between these. One of the major mathematics topics that was experienced is the concept of a function, especially linear.
To honor the goals, the students worked in groups of 3. The course met for three two hours laboratory periods, with no lecture, each week. Students' groups were given responsibility to carry out their work successfully with modest help from the instructor. Many of the experiments involved the microcomputer as a laboratory instrument for monitoring motion, and temperature related experiments. An example of a learning activity is given in Appendix A.
There were 29 students (18 Females, 11 Males) in the Spring of 1996. Eleven of the students were elementary education majors. The students are from different years in their undergraduate program. All students had completed at most one university mathematics course, and none had taken a university physics course.
During all lessons of Spring 1996 semester, one group was audio-taped. One of the researchers sat next to the group and wrote directly full transcripts. Unclear parts of these transcript were updated using the audio-tapes.
The group consisted of three female students: Mary (a 23 years old Caucasian), Jane (a Japanese student of 24 years old) and Anne (a 19 years old African-American and Hispanic). Mary and Jane took this course in the last semester of their undergraduate program, and Anne was a Sophomore. They all claimed in the beginning of the semester that they dislike and do not understand mathematics.
Analyzing the transcripts, we have observed that the lessons utilized two types of mathematical representations (graphical and algebraic) and two types of scientific situations (a real event and a story). Segments of a students' response to a question were classified according to the mathematical representations and the scientific situations that were dealt within them. The assignments that were given to the students served also as data to the research. The assignments were also classified according to the mathematical representations and the scientific situations that were dealt within them.
The different terms, used in the above papers, include both 'experiment' and a 'story' in them. We use the term 'experiment' in a limited context, as the actual physical event, that may include the process of carrying it out and collecting its results. The story is a description of a real or a an imaginary event. It summarizes the experiment with words and symbols.
We will give here two examples for stories and their matching experiments. The first example is drawn from the second lesson. In this lesson, students were provided with a description of a motion, "start 0.5 m from the detector, and walk from it with a slow steady pace." This description is a story that describes an experiment the students should try to carry out. The actual motion which the students performed is the experiment. Another example of a story is drawn from the sixth lesson. In question 1, Figure 1, the students were requested to write a story describing 9 stacks of washers. The actual stacking of washers, measurement of stacks, and collection of information is an experiment.
In this activity you'll place 2 cm stacks of washers on your lab table and examine the relationship between the number of stacks and the total number of washer on the table. Using a data table in your laboratory notebook, record the number of stacks and the total number of washer you've placed on the table as you place them on the table.
1. Predict the number of washers you would need in order to make 9 stacks of washers. Then, carefully explain the thinking process that you used to make your prediction. List each step in the process and explain its purpose.
2. Write an equation you could use to predict the number of washers in 9 stacks.
The experiments conducted in the lessons differed from stories in several characteristics. These characteristics are listed below.
[Jane measured a stack of 2 cm as three washers.]
Jane: There is no way we can actually get 2 cm with these washers.
Mary: And this is 1.9. [height of stack.]
Anne: Excuse me?!
Jane: This one is 2 cm.
Mary: Not quite, it's almost 2 cm. It's like a millimeter off.
Anne: Yea.
Jane: It should be, because we had big washers, not like other groups.
Mary: Oh, okay.
Jane: It should be 3 washers for 2 cm stack.
Mary: Okay.
The story did not necessarily contain boundaries. One might assume that the motion is infinite, and that the number of washers is unlimited. Some of the stories stated boundaries explicitly, such as the starting position for the motion, or the number of desired stacks.
We conclude that a story summarizes an experiment. Therefore, different stories may focus on and emphasize different characteristics of the experiment. That is, several different stories may summarize the same experiment. Since experiment includes detailed and raw information, several different experiments may be constructed to match to the same story.
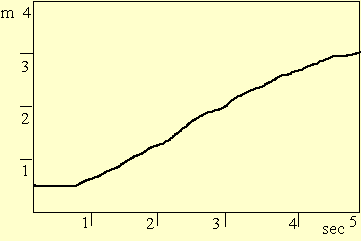
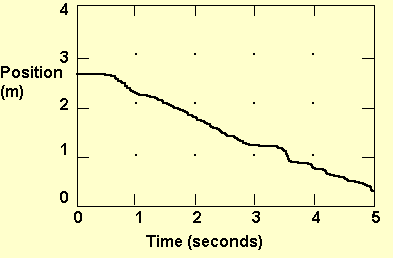
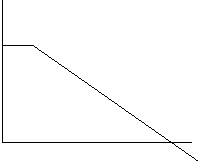
Graphs that were produced by experiment, included even more raw information, that is collected from the original experiment. For example, the graph in Figure 2, like the experiment that produced it, includes the information that the student hesitated in the beginning, and slowed down by the end. It also indicates that the motion is not steady. A linear equation that represents the same graph, such as d=0.5+0.6t or d=0.5+vt, does not include all of this information.
An algebraic representation may be defined for an unbounded domain. The algebraic representation, like a story, may include boundaries that are explicitly described.
We conclude that, as with the relationship between experiments and stories, many algebraic expressions may represent the same graph, and many graphs may represent the same algebraic expression. Schwarz and Dreyfus (1995) have already discussed this ambiguity in general. They claim that there is ambiguity between graphs and algebraic representations for several reasons: (1) graphs are partial they are limited in domain, (2) there is a limit to the accuracy of the graph drawing, (3) frequently the domain of an algebraic representation is not specified, (4) there is no unique formula representing a function. We would like to add that there is more ambiguity between graphs and algebraic representations that represent the same physical situation, because of the technological boundaries in obtaining the graph, and due to the fact that the graphs include much more detailed information, as described in this chapter.
Table 1
Observed characteristics of sensorial versus characteristics of symbolic representations.
| Characteristics of sensorial representations (experiments and graphs) | Characteristics of symbolic representations (stories and algebraic representations) |
| Sensorial, visual. | Verbal, symbolic. |
| Includes detailed raw information such as accuracy of drawing, moving ability, size, etc. | Idealization and summary of information. |
| Limited by physical boundaries such as space, time, domain limit, etc. | May be unlimited.
Boundaries may be specified explicitly. |
| Numerical data can be retrieved from it. | May include explicit numerical data. |
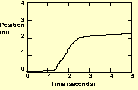
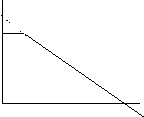
In the lessons, translations from an experiments to a graph and vise versa were based on technical skills. Beginning with the first lesson, students' obtained graphs that were derived from experiments using the micro-computer based laboratory. Within this lesson, the students realized the function of the motion detector, as Jane first remarked, "I don't know, because it detects like the position were the object is, right, I don't know, I'm just guessing." In the second lesson, the students developed a technique for obtaining a graph, similar to one already shown on the computer screen, by walking in front of the motion detector. The student that was walking in front of the detector looked at the computer screen to see the new graph that was created due to her own motion. She walked faster or slower, closer or further, and stopped for more or less time according to the differences between the graphs. Using a trail and error process, the student obtained a graph that is close enough to the target graph. After several lessons, the student obtained graphs in just a few trials. In the third lesson, Mary tried to obtain the graph shown as the dark line in Figure 3. She walked backwards while looking at the screen, forming the graph that is shown as a dotted line in Figure 3. Mary explained her error, "Too fast." Jane added, "You should stop and come back slower."

By the end of this lesson, Mary explained their method for carrying an experiment that will produce the desired graph:
TA: What do you need to do to make that curve?
Mary: You have the computer running, and then you try two or three times to get to it. But I don't know any other way.
TA: This is how you did it before?
Mary: Yes. But it was easy, because you had a point to stop.
In the beginning of the next lesson, Jane carried the same technique. She measured only where to start. The students repeated this technique in many more lessons.
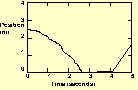
[Anne opens a file, and the graph with dark line in Figure 4 appears on the screen.]
[Jane brings a meter stick, and leads it on the floor away from the motion detector.]
Mary: Were are we starting from?
Jane: 1m. [Jane stands for few seconds and than begins to walk away from the detector. Figure 4 a appears on the screen.]
Mary: Try faster.
Jane: [Jane walks and the resulting screen is as Figure 4 b.] I'm starting too slow.
Mary: And then you stop.
[Jane walks and forms doted line and the resulting screen is as Figure 4 c.]
Mary: Yea, now you got it.
a. 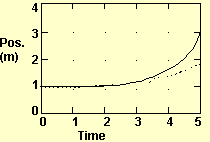 |
b.
|
c.
|
We conclude that the students had no difficulties during the lessons in translating between experiments and graphs. They used the computer to construct a graph that would match an experiment, and they developed a technique to construct experiment that will match a graph that appears on the computer screen.
y = ax +b, y = -.5x+3,
y = Position,
x= Time,
a = Constant pace or slope y/x,
b = Starting position or y intersect."
Later in this lesson, when asked "What is the physical meaning of slope?" Mary answered, "Slope, what does it mean now? It is constant pace." Jane confirmed, "I never thought what the slope is. Now it is," and she pointed on the group's white board. Anne also wrote the same answer in her notebook.
[Students read the question, where they are asked to draw the two patterns they predict that will be obtained by the two motions: (a) Start 0.5 m from the detector, and walk away from it with a slow steady pace, and (b) Start 1.5 m from the detector, and walk away from it with the same slow steady pace.]
Anne: You walk slowly.
[Mary draws Figure 5 a, in her notebook.]
[Jane draws like Figure 5 a, with dashed lines, in her notebook.]
[Anne draws Figure 5 b, in her notebook.]
Mary: Here you will get first and it will be flat.
Anne: I understand.
Mary: It's true.
Anne: You mean you will get their before.
Mary: Were going to test it.
[Students wait till other group clears their way.]
[Anne writes, "If you start at 1.5 then it will take shorter distance and less time than if you start at 0.5." Anne changes the lower graph to a linear function starting at 0.5 as in Figure 5 c]
Teacher: Can I see your prediction?
Mary: I don't know why did I did it, but it should be straight. [Mary changes the upper graph to Figure 5 d.]
Jane: The second goes like that. [Jane copies Mary drawing to her notebook.]
Mary: But we didn't have space.
[Anne changes her drawing to look like Figure 5 d.]
[Teacher goes.]
| a.
|
b.
|
c.
|
d.
|
[Students read the next question, where they are asked to draw the two patterns they predict that will be obtained by the two motions: (a) Start 0.5 m from the detector, and walk away from it with a slow steady pace, and (b) Start 0.5 m from the detector, and walk away from it with a medium fast steady pace.]
[Anne draws Figure 6 a, in her notebook]
[Mary draws Figure 6 b, in her notebook]
Jane: Didn't we do that?
Anne: The first one is the same.
Mary: The second is faster so you are going to hit first.
[Mary changes the upper pattern, and obtains Figure 6 c]
Teacher: How did you got this shape?
Anne: Move steady.
Jane: I hit the wall.
|
a. |
b.
|
c.
|
For example, in the seventh lesson students walked toward the detector in a constant pace and obtained a graph as in Figure 12, Appendix B, on the computer screen. Analyzing the graph, they were asked to "Predict what your position would be after walking for 13 seconds?" (Appendix A, question 6). The students related to a different motion than they actually performed, since they would have been out of the detector's range after 13 seconds. They answered the question as if they have walked from the detector (Appendix B, lines 61-69). That is, in order to obtain a story that will describe the experiment they have carried, students changed their interpretation of reality.
The students were asked in the same lesson to "Choose several 1.0 s time intervals and calculate your change in position during each," and to obtain an equation that will describe the graph as in Figure 12 (Appendix A, questions 5 and 7). The students changed the information obtained from the graph, so it will be linear (Appendix B, lines 47-60,77-81, 94-103). Even the teacher offered the students to examine a linear graph in order to obtain an equation that matches a non-linear graph they obtained before from an experiment (see line 112 and the graphs in Figure 13, in Appendix B). That is, in order to obtain an equation that will describe the graph they had, students interpreted the graph as linear, although it wasn't.
Jane: So at 2 seconds it starts moving.
[Mary takes the paper from Jane and writes on it the distance 3]
Teacher [talks to all the class]: I don't want you to get into to much details but some thing you do. You will be graded on your directions, not on your succeed.
Mary: O.K. 4 after 2 seconds.
Jane: This looks like 3½.
Mary: What are we going to do?
Jane: Constant pace. You walk ¾ m in a 1½ sec, in a constant pace.
Mary: We should mark this upon the floor, so we can know were to go.
[Mary writes step 1.5, step 4]
Jane: Do we need to explain what is a constant pace?
Anne: Just say which pace?
Mary: Slowly, for 1½ sec.
Jane: Towards the mark. O.K. as soon as you hit there.
In the tenth lesson, Mary uses words such as 'gradually' instead of giving precise descriptions. Later, after the teacher commented on a different story, Mary chose a more detailed description.
In a similar manner when describing a curve, such as that in Figure 2, by an equation some information may be lost. The students need to choose between simplicity of the equation to better fitness to the graph. (In the lessons we did not observed such hesitations, since the students mathematical knowledge was limited, and the lessons were restricted to algebraic representations by linear equations only.)
Jane: Two cm stacks means 3 washers.
Mary: So we need 27 of these?
Jane: Yes.
Anne: Three...
Jane: And we have just 11.
Anne: Yeah, but it doesn't say how many we already have.
Mary: This is nine stacks, so I guess we need 27.
Jane: Yeah, 27.
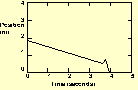
The students had also to extrapolate in order to carry the two motions: (a) "Start 0.5 m from the detector, and walk away from it with a slow steady pace", and (b) "Start 1.5 m from the detector, and walk away from it with the same slow steady pace." They extrapolated the obtained velocity-time graph that was obtained beyond the physical barriers that limited it. When Mary carried the experiment and obtained Figure 7, Anne explained "It went good, till you hit the wall," she explained the differences between the graph they obtained for the different stories, "Because we started further ahead and we had no room for that."
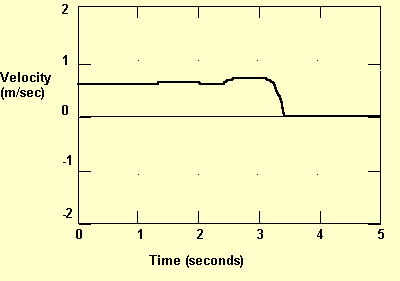
Fig. 7. Velocity-time graph obtained for the story, "Start 1.5 m from the detector, and walk away from it with the same slow steady pace"
Another example of extrapolation from a graph we bring from the eighth lesson. The students created by an experiment the graph that is presented by a dark line in Figure 8. For this graph they have found an algebraic presentation as d=3-0.5t. This graph is presented by a doted line in Figure 8. When the students were asked to compare the graphs, they claimed that the new graph was obtained from extrapolating the linear part of the original graph. They assumed that the starting position should have been 3 m away from the detector. Jane explained why they changed only the free-coefficient in order to obtain an equation that will match better the original graph, "Point 5 we found from the graph, but 3 we guessed."
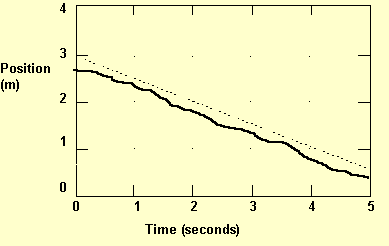
After translating the story into an experiment or a graph, the student had to determine whether the sensorial result in its boundaries and with the additional information matches the original story. The students most often decided to repeat the experiment and the graph construction, till it is sufficient. For example, in the seventh lesson the students were satisfied that the graph represents constant pace only in the fifth trial (Appendix B, lines 1-12). In the tenth lesson the students were asked to describe a motion that will result a graph as the dark line in Figure 9. Then they were asked to obtain the graph according to their description. Only the seventh trial was to their satisfaction:
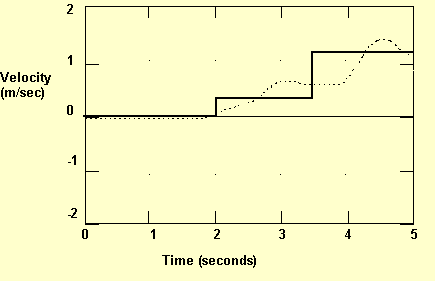
Jane: So, who's going to try this one?
Anne: I will. Okay, one minute. [Anne reads directions from her notebook.]
Anne: So basically I'm standing and then walk and then walk again.
Mary: No.
Anne: But it says stand still.
Mary: Then you...
[Anne walks. A graph with many noises is obtained.]
Jane: It was picking something else.
[Anne walks and obtains an almost linear graph.]
Jane: That was a little bit better.
[Anne walks and obtains a graph with many jumps on the last part.]
[Anne walks and obtains a graph almost linear.]
Jane: Can you see this? You were not looking.
Anne: I can, but it doesn't.
[Anne walks and obtains two curves, each reaching a step of the original graph.]
Jane: You run out of space.
Anne: You want to try?
[Jane walks and obtains a very low graph.]
Anne: Again.
[Jane walks and obtains Figure 9]
Anne: That's good.
Jane: Don't you want again?
Anne: That's basically the same shape.
In the fourth lesson, the students hesitated whether it is possible to create an experiment that will match the story. Whether it is possible to go back, stay there and return back to the detector, all within 5 seconds.
In the process of deciding whether the graph fits sufficiently the story, student become aware to causes of differences. For example, in the eleventh lesson Jane said, "We know that a wave is like a step, so it is okay," latter when constructing another graph she added, "I can't control the speed when I'm going so fast."
As a case study, one reform-based physics course that employs mathematical modeling, was observed. In the analysis of the observations we identified four situations -- experiment, story, graphical and algebraic representations. These situations are presented has vertexes of a parallelogram, in Figure 10. The upper situations in Figure 10 are considered as physical situations. The lower situations are mathematical representations.
In the lessons that were observed, the right situations in Figure 10 differed from the left situations. Experiments and graphs that were observed included detailed raw information, and they were bounded by physical constraints. Stories and algebraic representations serve as a summary of an idealized experiment or graph. They are unbounded, unless explicitly specified. Experiments and graphs are sensorial and visual, where as stories and algebraic representations are symbolic and verbal.
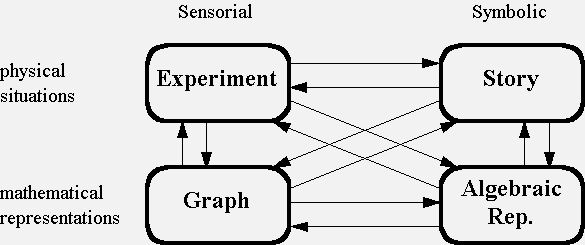
Each directed arrow in Figure 10 represents a possible translations. Between parallel arrows, with similar direction, many similarities were found. Vertical arrows were much more easier to carry than the horizontal ones, or the diagonal. In the lessons, the translation between a graph and an experiment and the translation between an algebraic expression and a story were technical processes. The students avoided translation between an equation and a graph, and preferred to translate between the equation to a story. They also avoided translating from a story to a graph, and preferred to translate the story to an experiment and from it to a graph. The right to left translations, as in Figure 10, also could be carried technically. However in these translations the students had to determine whether the obtained result is sufficiently close to the original situation. The left to right translations, as in Figure 10, where the most cognitive demanding. When creating a symbolic representation that will match a sensorial one, the students had to simplify the given situation and to extrapolate from it. They also had to determine whether the obtained result is sufficiently close to the original situation.
From this we conclude that when combining mathematics education with science education one should identify between different scientific situations.
Blum, W. & Niss, M. (1991). Applied mathematical problem solving, modeling, applications, and links to other subjects - state, trends and issues in mathematics instruction. Educational Studies in Mathematics, 22, 37-68.
Janvier, C. (1986). Translation processes in mathematics education. In C. Janvier (Ed.), Problems of Representation in Teaching and Learning Math, Library of Congress, Cataloging-in-Publication Data. p. 27-31.
Lesh, R. (1986). The evolution of problem representations in the presence of powerful conceptual amplifiers In C. Janvier (Ed.), Problems of Representation in Teaching and Learning Math, Library of Congress, Cataloging-in-Publication Data. p. 197-206.
National Council of Teachers of Mathematics [NCTM] (1989). Curriculum and Evaluation Standards for School Mathematics. Reston, VA: Author.
National Research Council [NRC] (1996). National Science Education Standards. Washington, DC: National Academic Press.
Schwarz, B. & Dreyfus, Teacher. (1995). New actions upon old objects: A new ontological perspective on functions. Educational Studies in Mathematics, 26, 259-291.
Authors
Gilli Shama, Physics Education Research Group, Department of Physics, University of Maryland, College Park, MD 20742-4111. e-mail: shama@seas.gwu.edu.
John Layman, Physics Education Research Group, Department of Physics, University of Maryland, College Park, MD 20742-4111. e-mail: jll5@umail.umd.edu.
1. What was your position at 3.5 seconds? How did you determine this position from the graph?
2. What was the time when you reached a position 2.5 meters away from the detector? How did you find this time from the graph?
3. How long did it take for you to move between the two positions 1.0 m and 2.5 m in front of the detector? How did you find this time interval?
4. How far did you move during the time interval from 1.5 s to 3.5 s? How far do you think you would move during a 1.0 s interval? Why?
5. Choose several 1.0 s time intervals and calculate your change in position during each. Record the time intervals, your calculations and your position changes in a data table. How do your position changes compare?
6. Predict what your position would be after walking for 13 seconds? Then, carefully explain the thinking process that you used to make your prediction. Is it significant that you walked at a constant pace? Why or why not?
7. Write an equation that describes the relationship between your position and the time. Show that your equation is correct.
8. What units are associated with each number in your equation? What physical quantity is each associated with?
9. Obtain each group's equation for position and record it in your laboratory notebook. Then write one equation that could be used by any of the groups? Under what circumstances is this equation valid? Why?
The lesson started at 9.00AM and ended at 10.50AM.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |