|
Readings in Physics from the UMd PERG: |
Although we are accustomed to using many types of numbers fractions, negative numbers, and irrational numbers like p or the square root of 2, it's really only the natural numbers or counting numbers (1, 2, 3, …) that have any natural meaning. The idea of counting seems to be hard-wired into our brains and into the brains of many animals.
Even with the counting numbers, there are subtle ideas that children only pick up about the time they go to school. One essential idea is that a count refers to an abstract property of a set of objects and that it doesn't matter how you arrange those objects. So if we define "4" to be the name that we assign to a particular set of objects by counting them, from the first to the last, the fact that 3+1 and 2+2 both give us the same result as a set of 4 is not entirely obvious.
Once I have the idea of addition, I can start to build equations which are equivalent to questions. What number do I have to add to 3 in order to get 7? This can be expressed as
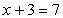
Once I have started to write equations, things get interesting, even when I only use the counting numbers. The equation above has a solution, but the equation
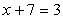
does not. Just for fun, I might invent a kind of number (called negative numbers) which satisfies this nonsensical equation and call it "-4". I could then easily show using the standard rules of arithmetic that this new kind of number will solve a lot of equations, such as x+9=5 or x+11=7. Indeed, every equation of this form will now have an allowed solution. Later, I might discover that these phony numbers in fact are useful in the real world say for keeping track of finances, where my assets are positive number and my debts are negative numbers.
We go through this same process a number of times in order to construct the numbers that you are used to working with. We get fractions when we need to invent numbers that will do the opposite of a multiplication or will describe the division of a set into equivalent parts. Here we have to decide carefully what we mean. For example, if we divide a set into two parts and take one of them, we say we have 1/2 of the set. If we divide the set in four parts and take two of them, we say we have 2/4 of the set. If we are working with a substance that can be partitioned and recombined without damage, such as water or money, then these are indistinguishable. As a result, we define a new "1/2" which is really the equivalence class of fractions 1/2, 2/4, 3/6, 4/8, etc.
Numbers like 2 orp are added to the collection of numbers by "filling in the gaps" that can be shown to exist between the set of all fractions. Any fraction can be shown to have a decimal representation which eventually starts to repeat itself, but we can certainly imagine processes which yield a decimal expansion that never repeats. Every non-repeating infinite decimal expansion is an irrational number one that cannot be represented by a fraction.
We can justify introducing complex numbers in the same way that we justified introducing negative numbers so as to be able to solve more equations. Once we have introduced them, we will find them of great value in describing physical situations in which there is an oscillation , such as AC circuits, Fourier analysis, polarized light, and quantum mechanics.
Solving algebraic equation can be an irritating business. If you start with a general nth order algebraic equation of the form
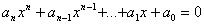
where the ai are constants (the subscripts are labels to specify different constants) and the xi represent the ith power of the unknown, x), you might find anywhere between no solutions and n solutions. A simple example is the pair of equations
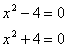
The first has two solutions: +2 and -2, while the second has none.
If we decide to try to extend our numbers so as to add solutions, we get a remarkable and satisfying result. We essentially have to add only one new number the square root of minus one, which we name i (or j). This is like adding the number "-1" to our counting numbers. In that case, all our negative numbers could be expressed as normal multiples of (-1); i.e., 10 = 10*(-1). Similarly, we can now express our complex numbers as a real part x and an imaginary part y, writing the entire number as
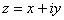.All of our standard arithmetic rules apply. The only additional rule we need is
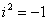.Exercise 1: Calculate the first six power of i with itself. Can you create a general rule for what in will be?
The value of introducing complex numbers becomes immediately clear when considering solutions to algebraic equations. We have the following important result:
The Fundamental Theorem of Algebra: Every nth order algebraic equation has exactly n roots if complex solutions are allowed.
This is of great importance in solving differential equations, since nth order linear differential equations with constant coefficients can be converted into algebraic equations by guessing a solution of exponential form eat . We then get an nth order algebraic equation for a. All we have to do is figure out what the complex solutions mean and whether they have any physical relevance.
In order to be able to make sense of complex numbers, we need two things:
An expression containing the sum of many complex terms is easy to put into standard form if each term is of the x+iy form. All we have to do is rearrange the terms in the sum, grouping all of the real parts together and all of the imaginary parts together. Thus, we have
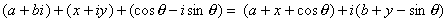
The situation only becomes tricky when we have an i in the denominator. This can be resolved by using the observation that for any a+bi, the product
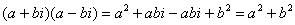
is a real, positive number (which cannot be zero unless both a and b are zero). We rationalize our complex denominators by multiplying by a useful form of one:
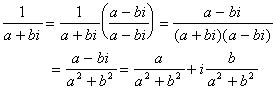
Since complex numbers correspond to two independent coordinates an x and a y we can try plotting a single complex number as a vector in a 2dimensional space. Let's just use the x part of the complex number as an xcoordinate and the y part as a y coordinate. Then we have the following pictures: the number "1" just corresponds to a vector of unit length along the positive x axis, the number "i" to a vector of unit length along the positive y axis, and a general number x+iy, to a vector from the origin to the point {x,y}.
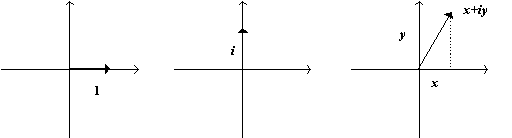
The use of the trigonometry of right triangles allows us to see that
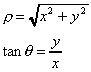
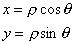(2)where r is the length of the vector, from origin to tip, and q is the angle it makes with the x-axis.
This becomes particularly useful when we note:
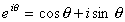(3)Exercise 2: Show that eqn. (3) is true by using the Taylor series for the exponential ex with x = iq. The trick is to regroup the terms in the series in standard form.
The fact that a complex number can be represented in polar form
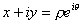(4)
helps us to understand where complex numbers are
going to be useful. If we want to represent circular motion,
where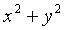 
is equal to a constant, the complex
representation will be of the vector of lengthr
swinging around the origin at a constant rate. This means that
we can use our understanding of uniform circular motion to represent
it asreiwt
where w
is a constant angular velocity. Taking the real and imaginary
parts of this expression gives us the oscillating x and y coordinates
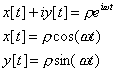
Whenever we have an oscillation, we have to worry about both its amplitude and its phase. Since we can write
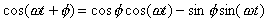
the relative amount of sin and cos oscillations tells us the phase. By keeping both the sine and cosine parts of an oscillation at the same time, a complex exponential lets us keep both amplitude and phase information at the same time with much simpler algebra - the algebra of exponentials.
The easiest way to think about how the complex exponential
handles the phase is to realize that when we use complex numbers
in linear equations with real coefficients, the real and imaginary
parts never interact. You can think of the use of complex numbers
in a second order differential equation as a way of handling both
of the two linearly independent solutions at the same time.
Maintained by University of Maryland PERG
Comments and questions may be directed to
E. F. Redish
Last modified October 1, 2000