Proceed to talk.

Student difficulties with math in physics: Giving meaning to symbols

Edward F. Redish, Richard N. Steinberg, and Jeffery M. Saul

Department of Physics, University of Maryland
College Park, MD 20742-4111

Presented 9 August, 1996 at the College Park meeting of the AAPT. Posted on the Web on 3 September, 1996.

Abstract

Although there have been studies on student understanding of the nature of science and science process, there has been little work on the implication of the role of student understanding of the symbology of physics on educational practice. We have seen a variety of difficulties that correspond to students having an incorrect understanding of the role of math in physics. Students can often perform mathematical operations correctly in the context of a math problem, but be unable to perform the same operations in the context of a physics problem. Students often have little appreciation for or understanding of the rich meaning carried by a symbol. We have seen a number of different kinds of failures of this type and will give examples and a preliminary classification of student difficulties with assigning meaning to the mathematics in a physics context.

The talk was originally designed to be presented using a browser (Netscape). Though it is all one document, the buttons can be used to present the talk in slide format. To get the proper size for a slide show, place the rainbow bar below at the top of your screen and adjust your window size so that this bar goes all the way across, and the height so that the next rainbow bar is at the bottom. If you are using a 640x480 screen, there should be no need to resize.














Proceed to talk.


Student difficulties with math in physics: Giving meaning to symbols

Edward F. Redish, Richard N. Steinberg, Jefferey M. Saul


Physics Education Research Group
University of Maryland, College Park

Supported in part by NSF grant RED-9355849

1

left arrowRight arrow2

Although there have been studies on student understanding of the nature of science and science process, there has been little work on the implication of the role of student understanding of the symbology of physics on educational practice.

In our studies of student expectations and epistemologies, we have seen a variety of difficulties that correspond to students having an incorrect understanding of the role of mathematics in physics.

Students may be able to perform mathematical operations completely correctly in the context of a math problem, but fail to understand the same operations when they occur in physics.

left arrowRight arrow3

We have observed a number of failures of this type

left arrowRight arrow3

Failure to see symbols as representing physical measurements rather than numbers

Students tend to want to substitute numbers into equations immediately, thereby simplifying the surface structure -- but destroying the deep structure. They therefore lose:

left arrowRight arrow5

Failure to note associated variations

For example, many students, when considering the force two interacting objects exerted on each other, will consider the equations
F=ma
F=MA

and will argue that the two forces must be different, either because the accelerations are different or because the masses are different, ignoring the fact that both change. (This is the analog of Piaget's conservation of quantity in studies of children.)

left arrowRight arrow6

Failure to be able to parse equations

Equations in physics often have a large number of arbitrary symbols. Math courses rarely use this many symbols -- and when they do there is usually a strict and systematic "code". The equation below is a typical physics example -- containing 6 distinct symbols.

Some students have trouble figuring out what are variables and what are constants in this expression.

left arrowRight arrow7

Additional difficulty is caused by the number of different kinds of "constants and variables" used in physics.

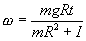
1. numbers2, e, 5/7
2. universal constantsc, h, k (Boltzmann)
3. experimental parametersm, R, T, k (spring)
4. initial conditionsx0, v0
5. independent variablesx, y, z, t
6. dependent variablesx, y, v

Notice the large number of "homonyms" distinguished by context.

left arrowRight arrow8

We also have "homoglyphs" -- symbols which look the same but mean different things. Imagine how hard this equation is to decipher for a student who doesn't notice diacritical marks!


In the expression above the parentheses is used for three distinct meanings. Note also that the string "(x,y,z)" appears twice -- with two different context-dependent meanings.

left arrowRight arrow9

Failure to coordinatize time and space

Students often do not understand how we use coordinates to quantify time and space. As an example, consider the following exam problem:

Exam question: A car is going around an oval track at a constant speed counterclockwise when seen from above. When it is at its northernmost point, draw vectors specifying the position, velocity, and acceleration of the car.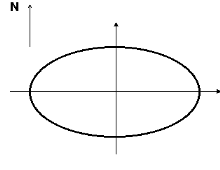

left arrowRight arrow10

Despite considerable effort in lecture (including telling the joke about the fisherman and the boat), about 25% of students in a calculus-based class for engineers missed this question on an exam, drawing the position vector in the same direction as the velocity vector. When interviewed, they showed that they did not understand coordinates as a description relative to some fixed reference point.

Many students said

Well, I know where he is. He's here (pointing to the top of the oval). But that's just a point. I need a direction to make a vector. The only direction I can think of to associate with it is the direction in which it is going, so I drew the position vector in the same direction as the velocity vector

left arrowRight arrow11

Failure to treat equations as representations of reality

In physics, equation don't simply stand for mathematical relationships. Physicists sometimes do not interpret equations solely by their mathematical content, but may interpret the mathematics using the physical context. Consider the following question on the photoelectric effect.

Exam question: Suppose you were to perform the photoelectric effect experiment using light of wavelength = 250 nm and an electrode made of nickel (phi = 5.2 eV). You find that when the potential difference measured across the electrodes V is equal to zero volts, the ammeter reads 0 current. Would the ammeter read zero or non-zero current if you replaced the nickel electrode with one made of aluminum (phi = 4.2 eV)? Explain your reasoning. (from Steinberg, Oberem, & McDermott)

left arrowRight arrow12


Nearly 1/4 of the students responded:

"The relevant equation is:"

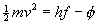So it will be non-zero. If (hf - phi) is zero, then changing phi makes (hf - phi) non-zero."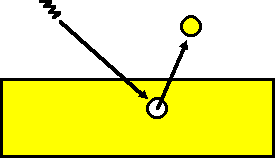


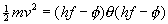
left arrowRight arrow13


What is happening, is that the equation really has the form


but most physicists don't need the theta function. Since they have a picture of the meanings in mind, they know that the equation only is meaningful when the kinetic energy is positive.

This sort of "implicit constraint" is often invisible to the teacher and unclear to the student.

left arrow14

This talk presented classifications of anecdotal evidence on student difficulties with the use of mathematics in university physics. Further details and specific research including the results of interviews and examinations is given in the next talk:

Student difficulties with math in physics: Why can’t students apply what they learn in math class?
Jeffery M. Saul, Michael C. Wittmann, Richard Steinberg, and Edward F. Redish

Click on the title to read this talk.

This page prepared by

Edward F. Redish
redish@quark.umd.edu

University of Maryland
Physics Department
College Park, MD 20742-4111
(301) 405-6120