Teaching Physics:
Figuring Out What Works

Edward F. Redish and Richard N. Steinberg
University of Maryland, College Park

Physics education research helps us understand what’s happening
in our physics classrooms and permits us to create more effective instruction.

This work was supported in part by NSF grants DUE 945 5561 and DUE 965 2877.

Introduction

Many physics faculty come away from teaching introductory physics deeply dismayed with how little the majority of their students have learned. Even worse, the growing importance of technological literacy in the workplace makes it increasingly important for us to provide value to more of our students.

Introductory courses are often designed for the prospective professional with many topics treated superficially to provide a context for later study, and with an emphasis on mathematical manipulations and structures. These mathematical structures may later serve as a framework for building a strong and well-organized understanding of the subject in which concepts and knowledge structure are tightly woven into the mathematics.

Most of our students, however, will not have the opportunity to study physics beyond a single course. More than 95% of students in introductory physics will never take another physics class. 1 Even engineers, many of whom will study the behavior of physical systems in their engineering classes, often use a distinctly different approach, and one which does not necessarily bridge the gaps that remain after introductory physics. The adage that "they need to see the material several times and then they will understand it when they teach it" is just not relevant to most of our students. Fortunately, evidence suggests that with the right kind of learning environment, a single pass through physics can be a valuable learning experience for the majority of students. 2

If we want to figure out what we can offer students in introductory physics (and beyond), we have to understand a number of distinct but interlocking topics. (1) What is involved in understanding and using physics? While this might seem obvious or even trivial to the professional, many of the components of our understanding are normally invisible to us. Careful observation and analysis of the physics content and of the behavior of experts is required. (2) What do our students bring to our physics classes? How our students hear and interpret the material presented to them in a physics class is heavily dependent on the experiences they bring to the class. Everyone has some sense that a force is necessary in order to maintain a velocity when walking, driving, or pushing something along the floor. Newton’s second law is inconsistent with the way that many of our students have made sense of their experiences in the world. (3) How do our students respond to our physics instruction? We often assume that students will respond as we did, or rather, as we might have wished we did, knowing what we know now. To design effective instruction, we must learn how students really respond.

A growing number of physicists are studying these topics, bringing together an analysis of the components and structure of physics knowledge with the observation and analysis of student behavior. The field of physics education research (PER) is a growing sub-discipline of physics.

Figuring out what works: Discipline-based education research

When it becomes difficult to make sense of a situation, we need to become researchers — to combine observation and analysis to figure it out. When the subject is our students, we become physics education researchers. At the heart of physics education research is a shift in emphasis in physics instruction from What are we teaching and how can we deliver it? to What are the students learning and how do we make sense of what they do? In order to make this shift, we need to listen to the students and find ways to learn what they are thinking. Only then do we begin to make sense of how students learn physics in a way that helps us improve our courses meaningfully.

What is required goes well beyond how even good teachers interact with their students. We both have observed classes and seen frequent cases where an instructor listened, but failed to recognize the student’s real difficulty. For example, in a junior level electronics class a student asked a question about a comparison of currents at two points on a single branch of a relatively complicated circuit. Like many physics instructors, the professor in this class was a concerned and dedicated teacher. He listened carefully to the student and recognized that the student was confused. But instead of asking questions to determine why the student was confused, he proceeded to give a detailed description of how the entire complicated circuit worked. However, since the current was necessarily the same throughout the branch of the circuit, it was likely that the student’s difficulty was a deep one — not addressed in the instructor’s response — that the current was "used up" en route. 3 The student politely nodded (no better off than before) and the teacher moved on.

In trying to find out what students’ real difficulties are physics education researchers use a variety of tools. One task is to determine the "state space" — the range of most common possibilities. . One way to do this is to carefully interview a number of students, letting them describe what they think about a particular situation or having them work through a problem. The researcher encourages the students to "think aloud" and to explain their reasoning. The goal is not to help the students come up with the "correct" answer but rather to understand their thinking. Interviews are videotaped, transcribed, and analyzed by multiple researchers. A photograph of a typical interview session is shown in Fig. 1. Interviews often reveal new insights into the way students think about physics that are surprising even to the most skilled and experienced instructors.

Fig. 1: Individual demonstration interview. In this particular interview, an upper-level physics major was asked about how conductors, insulators, and semiconductors would behave in a circuit. When left to explain what they really think about relatively simple tasks, students often reveal surprising beliefs about the physics that they have studied.

The information from interviews can be used to develop exam questions in which students are asked to solve problems and explain their reasoning or to write brief essays. A strong emphasis must be placed on having the students explain their thinking. Otherwise, they often replay poorly understood memorized patterns. Then, the evaluator might fill in the needed understanding from his or her own superior knowledge and fail to recognize where the students’ difficulties really lie.

After a good understanding of student confusions and difficulties is obtained, multiple choice tests or surveys can be carefully designed, with the distractors selected from common spontaneous student wrong answers. These tests and surveys can then be given to large numbers of students and distribution functions obtained. One needs to take care with the interpretation of these results since multiple choice tests or surveys give very limited views of complex situations. 4

Components of Problems Solving and the "Hidden Curriculum"

In a study of physics graduates in the workplace, the AIP found that problem solving was consistently rated as the most important skill learned in their undergraduate years. 5 In order to understand what is meant by "problem-solving", we have to look carefully at what it is that expert problem-solvers actually do . In the 1980’s, physicists, educators, and cognitive scientists carried out extensive studies of how different people approach physics problems. 6 As part of a study at the University of California at Berkeley (and later at Carnegie-Mellon University), Jill Larkin and Fred Reif contrasted the problem-solving approaches of an expert to that of an high achieving introductory physics student. 7 By "excellent student," they meant someone who was doing very well on the homework and examinations. Larkin and Reif characterize the expert’s problem solving as making use of, among other things, a strong understanding of physics concepts (what the physics is about), and a well-developed knowledge structure (how the physics fits together). In contrast, they characterize the student’s problem solving as being dominated by superficial mathematical manipulations without deeper analysis.

Can useful components of the expert approach to problem solving be successfully taught in introductory physics classes? When physics instructors describe what they are trying to teach in a physics course, they usually list the topics to be covered but don’t explicate the concepts, skills, or attitudes they hope their students will develop. Let us refer to those elements that we hope will be learned but which are not explicitly considered or described as the hidden curriculum .

Concepts

Since a good understanding of concepts seems to be a prerequisite for expert problem solving, much effort has gone into the identification of fundamental concepts and student difficulties in a variety of specific areas. For the past 20 years, Lillian C. McDermott and the Physics Education Group at the University of Washington have been leaders in carrying out this research. 8

McDermott and other physics education researchers have documented that even after studying physics, student understanding of fundamental concepts is often weak. For example, the study detailed in Sidebar 1 shows some of the difficulties students have in making sense of the concept of a photon. (See references 9 and 10 for further details.) Note that the interviewed students might well be able to answer standard problems on the photoelectric or the Compton effect. However, the way they think about the photon inhibits the way they make sense of the nature of light.

Evaluating how well students have learned the basic concepts requires the use of the full range of PER observation tools: interviews, open-ended exam questions, and carefully constructed multiple-choice tests. In order to study distribution functions and student responses on a large scale, the last is the easiest to deploy.

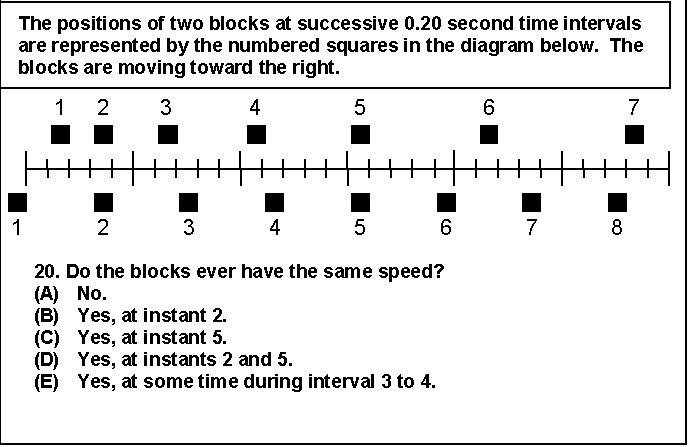
David Hestenes and his colleagues at Arizona State University have developed the most extensively used multiple-choice diagnostic to date. 11 The Force Concept Inventory (FCI) is a 29-question test that has helped increase the awareness of the extent of student conceptual difficulties in mechanics. Basic concepts from introductory mechanics are covered, but the wording is couched in common speech rather than in that of a typical physics problem. The distractors are chosen based on the most commonly held incorrect beliefs as determined by interviews and open-ended problems. Sample questions from the FCI are shown in Fig.  and in Sidebar 2.

Fig. 2: Question 20 from the Force Concept Inventory. Half the students answer this incorrectly both before and after traditional instruction. However with a research-based active-learning environment we see that student conceptual learning can be much improved.

Student difficulties distinguishing a quantity from its rate of change are persistent throughout all of introductory physics. This causes trouble both when students learn kinematics (confusion of velocity and position) and dynamics (confusion of force and momentum). Although most students can state that velocity is "the derivative of the position," their understanding is often a superficial parroting of terms that they have encountered.

At the University of Maryland, we administered the FCI to 16 different lecture classes over 5 years. In this study, 767 students completed the FCI both before and after instruction. Of these students, 238 had traditional instruction and 529 had modified instruction (described below). Prior to any instruction, only 50% of the students gave the correct answer to the item shown in Fig 3 (choice E). Most of the students answering incorrectly appeared to focus on the instant when the blocks are at the same position, not when they are moving at equal velocities. Obviously, teaching this material is an important part of instruction during the mechanics part of the course. Unfortunately, after traditional instruction the success rate was 47%. Similar results are seen in other examples (see Sidebar 2).

It is important to note that the student difficulties that we observe are not limited to their performance on multiple choice items. In fact, looking merely at student performance on multiple-choice diagnostics can be very misleading. 4 However, results comparable to those described in the previous paragraph have been observed using other tools, including open-ended questions, problems, and interviews. 12

Expectations

The studies of expert problem solvers indicate that there is much more to being a good problem solver than agility with mathematical manipulations and a good knowledge of concepts. For many students in introductory physics, the idea that concepts are relevant to problems or that physics is more than a set of facts and equations to be memorized is missing. These difficulties do not necessarily go away, even given our "ideal" situation ¾ physics majors trained for graduate school. We have heard numerous (but anecdotal) complaints from advisors of physics Ph.D. students who approach their research by "turning the crank" without thinking about the physics.

In a study at the University of California at Berkeley, David Hammer carefully investigated the views about the nature of the physics knowledge of a small number of students in a calculus-based physics course. 13 He interviewed students throughout the course and observed how they approached complex problems. He found that most of the students had attitudes about the nature of physics and how one approaches problems that were counterproductive to helping them develop a strong understanding of physics or expert problem-solving skills. He classified their beliefs along three dimensions: independence/authority, coherence/pieces, and concepts/equations. In order to probe the distribution of these attitudes in large calculus-based physics classes, we have developed the Maryland Physics Expectations (MPEX) survey, a set of 34 statements that students are asked to agree or disagree with. 14 These probe the Hammer dimensions and three more: a physics-reality link, a math-physics link, and an effort variable. (See Table 1.) We describe these views as "cognitive attitudes" or expectations .

	Favorable	Unfavorable
Independence	Learns independently, believes in their own need to evaluate and understand	Takes what is given by authorities (teacher, text) without evaluation
Coherence	Believes physics needs to be considered as a connected, consistent framework	Believes physics can be treated as separated facts or "pieces"
Concept	Stresses understanding of the underlying ideas and concepts	Focuses on memorizing and using formulas
Reality link	Believes ideas learned in physics are useful in a wide variety of real-world contexts	Believes ideas learned in physics are unrelated to experiences outside the classroom
Math link	Considers mathematics as a convenient way of representing physical phenomena	Views the physics and the math as independent with no strong relationship between them
Effort	Makes the effort to use information available to them to modify and correct their thinking	Does not use available information about their own thinking effectively

Table 1: Dimensions of student "expectations." Student attitudes can be at either extreme or somewhere in between. Unfortunately, we have seen that, on the average, the percentage of students with favorable attitudes tends to deteriorate as a result of traditional instruction.

We presented our survey to a group of expert physics instructors and asked them to choose the answers they would like their students to give. The experts agreed on the polarity (whether the students should agree or disagree) of the responses nearly 90% of the time. We refer to a student opinion that agrees with the expert polarity as favorable and to one that disagrees as unfavorable .

In our study of student expectations, we find that after three semesters of traditional instruction in calculus-based physics, half of our engineering physics students agree with the following statement from the MPEX survey:

Our instructors carefully present critical derivations in lecture. They use them to show the applicability of the resulting formula and its relation with fundamental principles. Nonetheless, many of our students choose to ignore the teacher’s explicit emphasis. Their view of what they expect to get out of the class is the use of formulas, not an understanding of the limitations of those formulas or the relation of the formula to fundamental principles and concepts.

Building Research-Based Curricula

In response to the elucidation of specific student difficulties learning introductory physics, a number of physicists have produced curricula that specifically focus on teaching more effectively. In building these research-based curricula, developers combine two elements. They use their understanding, learned from PER, as to what difficulties students really face. These are combined with educational structures and environments influenced by scholars of education and cognitive psychology who find that most students learn more effectively in active-engagement environments in which social interaction takes place. 15 Finally these are refined through successive delivery, research, and redesign.

Detailed descriptions of many research-based curricula may be found in the second volume of the Proceedings of the International Conference on Undergraduate Education. 16 We evaluate two specific examples of research-based curricula and traditional instruction below.

Traditionally, introductory physics at large research universities is taught in large lecture classes (2-4 hours/week), small group recitations (1-2 hours/week), and laboratories (2-3 hours/week). Lectures are usually presented by a faculty member with little or no student participation. Lectures may include demonstrations and the modeling of the solution of sample problems. Recitations are often presented by teaching assistants (TAs). They may answer student questions, but the activity tends to have the TA modeling solutions to the problem on the board. Students rarely participate actively.

At the University of Washington, Lillian McDermott and her collaborators have developed a replacement for the recitation in traditional introductory classes called tutorials . 17 Instead of watching TAs modeling problem solving, students work in groups of 3 or 4 on carefully designed research-based worksheets. In these worksheets, students are led to make predictions and compare various lines of reasoning in order to build an understanding of basic concepts. TAs serve as "facilitators" rather than as lecturers. Help with textbook problems is available in extended office hours. In addition to a lecturer, this model requires approximately one facilitator contact hour per week for 15 students.

Fig. 3: Interactive computer-based tutorial on force and motion. Students are up and around and actively participating in this classroom lesson where a motion sensor is used to provide real time graphs of position and velocity.

At Dickinson College, Priscilla Laws and her collaborators have developed Workshop Physics — instructional materials for a non-traditional learning environment in which lectures, recitations, and laboratories are combined in two 3-hour lab-based sessions. 18 Students work in groups of 2-4 with sophisticated computer equipment that permits them to obtain high quality data quickly and efficiently. They are led by an activity guide to build fundamental concepts and laws through guided observation and discovery. This model requires an instructor and an assistant (such as a student who has successfully completed the class) for about 30 students for 6 contact hours per week.

Note that in tutorials, only one hour per week is changed, while the lecture, lab, and text remain traditional. In Workshop Physics, the entire course structure is modified.

Evaluating Research-Based Curricula

At the University of Maryland, we have recently completed a project studying the results of one semester of calculus-based physics in three educational environments: traditional, a traditional environment modified to include tutorials, and Workshop Physics. 12 We evaluated students’ conceptual learning, the evolution of students’ cognitive attitudes towards physics, and their traditional problem solving abilities.

We evaluated the effectiveness of conceptual learning with a variety of tools including

• detailed student interviews,
• open-ended examination problems, and
• multiple-choice diagnostics.

While each method provides different insights, the results of the different probes have been consistent. For brevity, in this section we will focus on the results obtained with the FCI.

It should be noted that while coverage is comparable to a traditional course, tutorials, Workshop Physics, and many other innovative learning environments emphasize conceptual learning. However, the concepts covered on the FCI (such as acceleration and force) are widely recognized as universally important to learning introductory mechanics. One might be concerned that the extra effort spent on concepts in the research-based courses might be at the cost of other learning goals, such as problem solving. However, student problem solving skills and expectations in research-based learning environments are as good or better than in the traditional classes. 3 , 9 , 12

Richard Hake at Indiana University studied student performance on the FCI. He collected FCI reports before (pre) and after (post) instruction from more than 6500 students in 62 introductory physics classes. 19 Hake found that interactive engagement classes using PER-based curricula consistently had higher gains on multiple choice diagnostics. He also found that although classes at different institutions had widely different pre-FCI scores (ranging from 25%-75%), courses with a similar structure had a similar fraction of the possible gain ; that is, the Hake factor

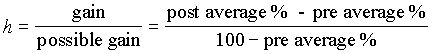
serves as an appropriate figure of merit.

In our study at the University of Maryland, we collected pre and post FCI scores in a calculus-based physics course both in a traditional class with recitations and the identical class but with tutorials. During a 5-year span, about half of the lecture classes were done in each mode, with students not being aware beforehand which model was to be used. We collected matched data from a total of 767 students with ten different lecturers. Seven classes were done with recitations and nine with tutorials.

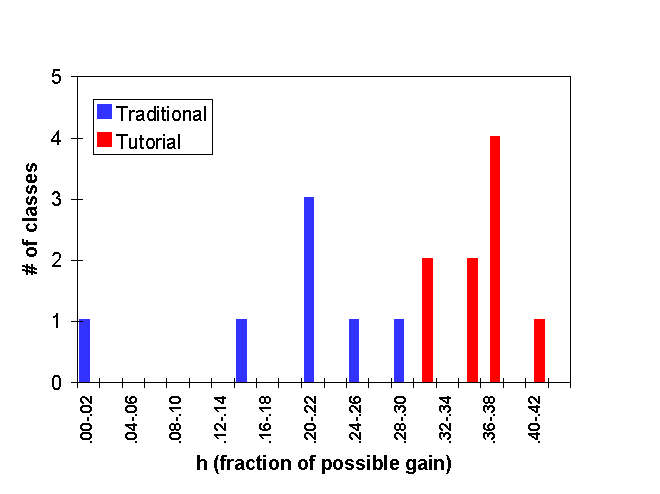
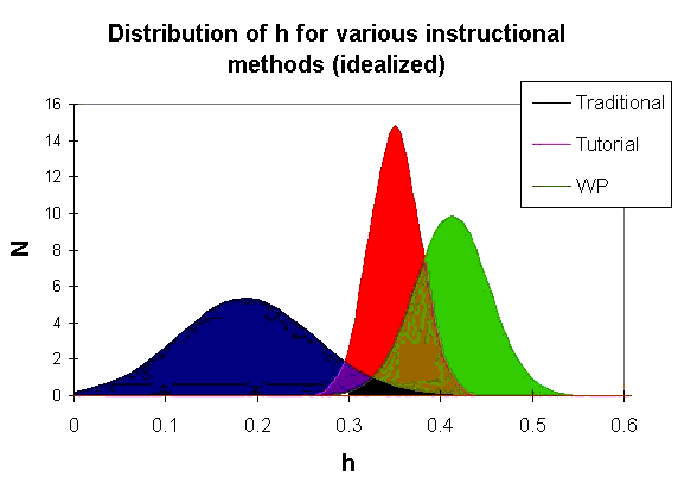
The FCI was administered as an ungraded quiz during the first and last week of the course. We display the fractional gain in Fig. 4a. Two of the lecturers taught in both modes. These instructors found that their classes h factor improved by more than 0.15 when they used tutorials. We extended our study to more than 2000 matched students at 7 additional institutions, including a number who were introducing the Workshop Physics curriculum. Our results show a Hake factor of 0.16 ± 0.03 for traditional curriculum, 0.35 ± 0.03 for traditional with tutorials, and 0.41 ± 0.02 for Workshop Physics classes. These results are displayed in Fig. 4b by replacing the histograms with Gaussians adjusted to fit the mean and standard deviation of the distribution and normalized to unity. While it is encouraging that higher gains are possible, it is important to recognize that they are still much less than one.

Fig. 4: (a) Histogram of FCI gains in traditional and tutorial classes at the University of Maryland. (b) Gaussian fit to histogram of FCI gains in traditional, tutorial, and WP classes at 8 institutions. It is clear that student performance is better after going through research-based learning environments than it is after going through traditional learning environments.

We used the MPEX survey to probe the distribution and changes in student cognitive attitudes. Based on the results from more than 1500 students from 6 colleges and universities, it is clear that many students come into physics with unfavorable views about the nature of learning physics. Before instruction the students made choices of polarity that concurred with those of our experts only about 60% of the time. More worrisome is that these views tend to deteriorate after a traditional semester of university physics. On the important items measuring independence, coherence and concepts (see Table 1), the starting values were closer to 50%. After one semester of instruction in mechanics, almost no traditional or tutorial classes showed improvement in any of the variables. Indeed, the overall average of 1350 (pre-post matched) students at 3 large research universities deteriorated by about 1 s after one semester of instruction.

However, it does appear that in certain modified learning environments student views do evolve to be more favorable. In the Workshop Physics classes we studied, students showed a 2.5 s improvement on the average of the independence /coherence /concepts clusters. This is displayed in Fig. 5. In this plot, the percentage of students agreeing with the favorable response is plotted on the abscissa, and the percentage giving unfavorable responses is plotted on the ordinate. Since the sum of favorable, unfavorable, and neutral must add up to 100%, the plotted points must lie in the triangle bounded by the points (0,0), (100,0), and (0,100).

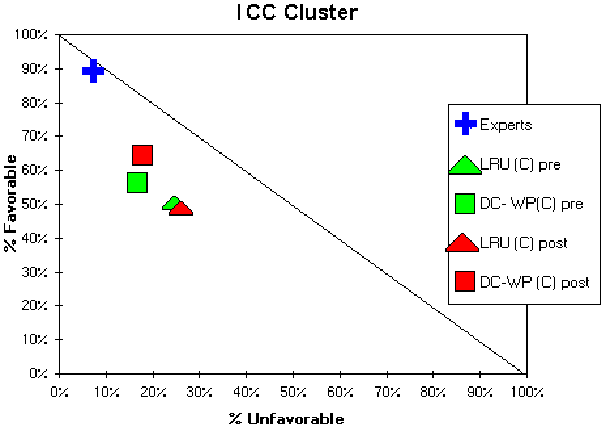
Fig. 5: Average results on the Independence/Coherence/Concepts variables described in Table 1. Results were determined using the MPEX survey given at the beginning and end of the first semester of introductory calculus-based physics at Dickinson College (Workshop Physics [WP]) and three large research universities [LRU] (traditional or tutorial). Students' attitudes along these dimensions seem to deteriorate after traditional instruction but improve slightly after Workshop Physics.

Conclusion

Over the past two decades, an increasing number of physicists have been turning their research attention to problems of physics education. About one dozen physics education research programs now exist in research physics departments around the country. One benefit of this is to bring a physicist’s perspective and expertise to the study of how to make our physics classes work effectively. A physics department benefits from the development of more effective teaching methods tuned to their particular situation, and by building links to other physics education researchers.

In this article we have discussed the findings of the physics education research community on two of the elements students need to master in order to become expert solvers of complex problems: concepts and appropriate cognitive attitudes. This is by no means the whole story. Additional research is still needed on many topics, including: students’ ability to apply concepts in problems, their reasoning and use of mathematics, and the impact of technological environments on what students learn. But the by-now large body of physics education research (reference 2 cites more than 200 items) has provided many solid and surprising insights that can help physics instructors improve their judgments about what is happening in their own classrooms. This research has led to a variety of curricular tools and techniques that can help instructors deliver more effective instruction (see reference 16). But what is perhaps most important is that the dialog within the physics community on what is effective in instruction is now well begun. We have started the process of growing, evaluating, and cumulating a solid set of community knowledge on what works — and what it means for instruction to work.

What was Dirk really thinking about light after successfully completing introductory calculus-based physics? In order to find out, I showed Dirk a small bulb, a piece of cardboard with a rectangle cut out, and a sheet of paper. 9 "What would you see on the paper if the room light were turned off and the little bulb on?" (I never did the experiment, I just asked what if.) Dirk drew a picture of perpendicular sine curves and called one the "electric flux" and the other the "magnetic part." A strange approach given that the problem can be easily solved with a ray diagram. "So what would you see on the screen?" Dirk eventually drew straight lines and came up with the correct response. "What if the slit were narrower?" Dirk said that geometrical optics applies as long as the slit is wider than the wavelength of light because "the waves are still making it through the slit." Not only is this answer incorrect, but this is an unusual way to describe light. "What if the width of the slit were a little bit less than the wavelength of the light?" Dirk stated that now a diffraction pattern occurs; the magnetic part of the wave will not "be affected" but the electric part "will be affected … [the slit] knocks it out of whack." Dirk explained how the amplitude of the electric wave hits the sides of the slit causing the diffraction, but the magnetic part of the wave gets through because it is lined up with the long dimension of the slit.

We interviewed 48 students who had finished introductory calculus-based physics. Most were among the best in the class. During each interview the goal was to probe what the student was thinking while trying not to affect what s/he was thinking. Students were asked to make predictions and explain their reasoning. In accounting for their predictions, about half of the students had some sort of spatial interpretation of the amplitude of light. The figures show two examples. Most of the other students did not do as well as these two.

This type of research has guided the development of tutorials . 10 For physical optics, students supplement the standard mathematically oriented textbook / lecture by making observations of water waves propagating freely and through slits of various widths, applying principles of superposition when there is more than one wave present, and building an analogy with the behavior of light. Students build an understanding of the different models they are using, and consider both the values and limitations of the models. There is an emphasis on reasoning required for the development and application of important concepts and principles.

In some lecture classes at the University of Maryland, tutorials have replaced the traditional quantitative recitation sections. Not surprisingly, we found that tutorial students did better on conceptual / qualitative questions. However, we also found that tutorial students also did considerably better on a standard textbook like problem (60% vs. 16% correct). 9 R. N. Steinberg

In one of my engineering physics classes, I gave this question on Newton’s third law from the Force Concept Inventory 11 on the final exam. One of my better students came to my office after the exam and was very upset. She expressed her confusion about which of two colliding vehicles felt the greater force, a small car, or a large truck and reported that she had changed her answer numerous times during the exam. "I know," she said, "that Newton’s third law says they should be equal, but that can’t be right, can it?" The classroom context led her to bring up her "physics class" model, Newton’s third law, but the common-speech wording of the question led her to bring up her common sense response, larger objects exert a larger force. Successfully learning Newton’s third law was not enough for her to be comfortable with the situations in which it should be used.

When this problem was given to large numbers of Maryland students as a pretest, only 30% chose the correct answer, (E), with 66% of them choosing answer (A). After recitations, the number of correct answers rose, but only to 50% with half of the students still giving answer (A). After tutorials, the number of correct answers rose to 80% with only 20% choosing answer (A). (N = 238 for recitations, N = 529 for tutorials.) E. F. Redish

Notes