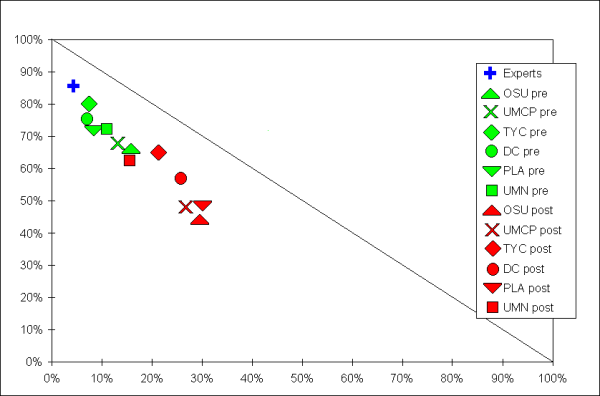
Fig. 3: A-D plot for all schools, effort cluster
To return to part 1 of this paper, click here.
To return to part 2 of this paper, click here.
To return to part 3 of this paper, click here.
Most of the schools begin with favorable responses on item #4 of 50-55%. Our TYC is an anomaly, with only 16% of the students responding favorably on this item. This suggests that the group of students in our TYC may be considerably less sophisticated, at least along this dimension, than the average beginning university student. The shifts on this item tend to be favorable and significant (e.g., UMCP 47% 59% favorable, DC 52% 64% favorable) with the exception of our PLA institution which showed a shift towards neutral.
All groups showed a low initial favorable response on item 19 (13% (TYC) to 31% (UMN)) but all showed a shift towards the favorable by the end of the semester.
Although physicists believe that they are learning about the real world when they study physics, the context dependence of cognitive responses (see ref. 5) opens a possible gap between faculty and students. Students may believe that physics is related to the real world in principle, but they may also believe that it has little or no relevance to their personal experience. This can cause problems that are both serious and surprising to faculty. The student who does a calculation of the speed with which a high jumper leaves the ground and comes up with 8000 m/s (as a result of recalling numbers with incorrect units and forgetting to take a square root) may not bother to evaluate that answer and see it as nonsense on the basis of personal experience. When an instructor produces a demonstration that has been "cleaned" of distracting elements such as friction and air resistance, the instructor may see it as displaying a general physical law that is present in the everyday world but that lies "hidden" beneath distracting factors. The student, on the other hand, may believe that the complex apparatus is required to produce the phenomenon, and that it does not occur naturally in the everyday world, or is irrelevant to it. A failure to make a link to experience can lead to problems not just because physics instructors want students to make strong connections between their real-life experiences and what they learn in the classroom, but because learning tends to be more effective and robust when linked to real and personal experiences.
The four items we have included as the reality link cluster (items 10, 18, 22, and 25) do not just probe whether the students believe the laws of physics govern the real world. Rather, our items probe whether the students feel that their personal real world experience is relevant for their physics course and vice versa. In our interviews, we observed that many students show what we would call, following Hammer, an "apparent reality link." That is, they believe that the laws of physics govern the behavior of the real world in principle, but that they do not need to consider that fact in their physics class.
Our three groups of instructors were in almost unanimous agreement (93-95%) with the favorable response on our reality cluster. An interesting anomaly was the response of the USIPOT students who only gave favorable responses at the 64% level. Examining their written comments as well as their responses gives one possible explanation: A significant number of USIPOT students saw physics as being associated primarily with interesting and exotic phenomena, such as cosmology, relativity, and particle physics. Some of these students did not see a link between this physics and their personal experiences.
The student groups at our six schools started out with fairly strong favorable responses, ranging from 61% (UMCP) to 76% (DC). Unfortunately, every group showed a deterioration on this measure as a result of instruction, and some of the shifts were substantial (OSU from 65% to 54%; PLA from 71% to 52%, and TYC from 69% to 58% favorable responses).
An important component of the calculus-based physics course is the development of the students' ability to use abstract and mathematical reasoning in describing and making predictions about the behavior of real physical systems. Expert scientists use mathematical equations as concise summaries of complex relationships among concepts and/or measurements. They can often use equations as a framework on which to construct qualitative arguments. Many introductory students, however, fail to see the deeper physical relationships present in an equation and instead use the math in a purely arithmetic sense -- as a way to calculate numbers. When students have this expectation about equations, there can be a serious gap between what the instructor intends and what the students infer. For example, a professor may go through extensive mathematical derivations in class, expecting the students to use the elements of the derivation to see the structure and sources of the relationships in the equation. The students, on the other hand, may not grasp what the professor is trying to do and reject it as irrelevant "theory." Students who fail to understand the derivation and structure of an equation may be forced to rely on memorization - an especially fallible procedure if they are weak in coherence and have no way to check what they recall.
The survey items probing students' apparent expectations[29] of the role of mathematics are 2, 6, 8, 16, and 20. Our expert group is in strong agreement on the favorable answers for this cluster, agreeing at the 92% level. Since high school physics courses tend to be decidedly less mathematical than university physics courses, we were not surprised that the high school instructors have much lower expectations for their students on this cluster, agreeing with its elements only 67% of the time. This is comparable to the initial percentages of most of the students in our test classes, which range from 58% to 74%.
Although these lower expectations may be appropriate for high school students and therefore for beginning university students, one might hope that these attitudes would change towards more favorable ones as a result of a university physics class. Unfortunately, none of the classes probed show improvement in the favorable/unfavorable ratio and three (UMCP, OSU, PLA) show a significant and substantial deterioration.
Among the items of the cluster, the results on item 2 is particularly interesting.
#2: All I learn from a derivation of a formula is that the formula obtained is valid and that it is OK to use it in problems.
From our interviews and informal discussions, we note that many students today have had little or no experience with formal mathematical proof. A few did not understand the meaning of the word "derivation," mistaking it for "derivative."[30] This lack of experience can produce a severe gap between the expectations of instructors and students and cause serious confusions for both groups. On item 2, the students at no institution showed favorable responses (disagree) at higher than the 44% level (UMN). At our TYC, only 20% gave a favorable response with item 2 initially, and 48% of the students gave the unfavorable response. (We write this response as 20/48.) They improved somewhat after the class (to 33/41), but our PLA deteriorated significantly (from 36/18 to 25/33). This deterioration did not appear to be associated with the Workshop Physics structure which tends to emphasize hands-on and laboratory activities over purely abstract and mathematical reasoning. The DC students changed on item #2 from 39/25 to 45/31. This maintains approximately the same ratio, but fewer students are undecided.
Many physics lecturers do not expect most of their students to follow what they are doing in lecture during the lecture itself. They expect students will take good notes and figure them out carefully later. Unfortunately, many students do not take good notes and even those who do may rarely look at them. When physics begins to get difficult for students, most instructors expect them to try to figure things out using a variety of techniques - working through the examples in the book, trying additional problems, talking to friends and colleagues, and in general trying to use whatever resources they have available to make sense of the material. Some students, on the other hand, when things get difficult, may be at a loss for what to do. Some students do not have the idea that if they do not see something right away, there are steps they can take that will eventually help them make sense of the topic.[31] An important component of the tools that help build understanding is the appreciation that one's current understanding might be wrong, and that the mistakes one makes can give guidance in helping to correct one's errors. This dimension is probed by items 3, 6, 7, 24, and 31 on the survey.
For this cluster, the results are striking enough that we display them in an A-D plot in Fig. 3. Our experts are in strong agreement on the answers to the items of this cluster, at an 85% level. The initial views of the students at the various institutions begins quite high, ranging from 66% favorable (at OSU) to 80% favorable (at our TYC). By the end of the semester, the shift is dramatically downward, with three institutions dropping in the favorable percentages by 20% or more (UMCP, OSU, and PLA), and three dropping by 10-15% (UMN, DC, and TYC). In one sense, this may be interpreted that the students expected to make more of an effort in the course then they actually did, as the shifts were largest on items 3 and 6, but the downward shifts on items 24 and 31 were also substantial.

Every finite set of data contains fluctuations which have no real significance but arise from the details of a particular sample. In this paper, our research questions involve comparisons of groups - experts and novices, novice students at different institutions, and students at the beginning and end of their first semester of physics. In order to compare these groups, we are comparing their averaged responses (agree vs. neutral vs. disagree). In order for us to understand whether two responses are significantly different, we have to have some model of the random variable in our sample.
Our interviews, our intuitions, and many discussions in the cognitive literature suggest that a human attitude is a highly complex object. As we noted above, some students gave clear evidence in interviews of being in two contradictory states at the same time. What this implies is that the random variable we should be averaging is itself a probability, rather than a set of well-defined values. Unfortunately, the average of probabilities may depend significantly on the structure of the constraints and parametrization of the probabilities, as is well know from quantum statistics. Since detailed models of student attitudes do not yet exist, we will estimate our significances by using a cruder model.
Let us assume that a class is drawn from a very large homogeneous [32] group of students and that in the large population, a percentage p0 of responses to an item or cluster will be favorable and a percentage q0 will be unfavorable with p0 + q0 1. (For now, we will ignore the possibility of neutral responses. [33]) In a finite sample of n students, we want to know what is the probability of finding n1 favorable and n2 unfavorable responses with n1 + n2 1. Using the Gaussian approximation to the binomial distribution, we get that the probability of finding fractions p = n1/n and q = n2/n is
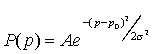
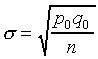
For this distribution, the probability that a sample will have a mean that falls within 1s of the true mean, p0, is 0.684 and the probability that a sample will fall within 2s of the true mean is 0.954.
Since the fraction of neutral responses tends to be small, and
since the binomial model is crude for this set of data, we treat
our trinomial data as if it were approximately binomial by renormalizing
the observed p and q into 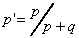 and
and 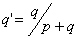 .
We consider a difference or shift in means to be significant if
it is at less than the 5% probability level, that is, if the difference
or shift is greater than twice
.
We consider a difference or shift in means to be significant if
it is at less than the 5% probability level, that is, if the difference
or shift is greater than twice 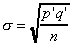 . For example,
at values of p = 60%, q = 20% for N = 450,
we get s ~ 2%. This doesn't change
much over the typical values of p and q seen in
Table 4. We therefore consider a 5% shift to be significant for
our large schools. For N = 115, those values of p and q
give s ~ 4%. We therefore
consider a 10% shift to be significant for Dickinson.
. For example,
at values of p = 60%, q = 20% for N = 450,
we get s ~ 2%. This doesn't change
much over the typical values of p and q seen in
Table 4. We therefore consider a 5% shift to be significant for
our large schools. For N = 115, those values of p and q
give s ~ 4%. We therefore
consider a 10% shift to be significant for Dickinson.
In this paper we have discussed the creation and use of the MPEX survey of student cognitive attitudes in physics. The survey was constructed to probe student expectations with a focus on six structures: independence, coherence, concepts, the link between physics and the real world, understanding of the role of math in physics, and the kind of effort they expect to make. The survey was calibrated using five groups. The group expected to be most sophisticated was in strong agreement (better than ~80% on almost all the items) as to the desired responses on the items of the survey and their preferred response was defined as favorable. The other calibration groups showed increasing agreement with the expert group in the predicted manner.
We tested the survey in classes at six schools that had varying entrance selectivity and that used a variety of approaches. We find explicit answers to the research questions we posed in the introduction.
At the six schools tested, the initial state of students deviated significantly from that of the expert calibration group with overall responses ranging from 50-60% favorable. The results on the concept cluster were particularly low (30-45%) and on the reality cluster were particularly high (60-75%).
At our three large state flagship institutions (UMCP, OSU, UMN) student attitudes as measured by the survey were very similar. The attitudes of beginning students at our selective liberal arts institution (DC) were consistently more favorable and those at our two year college (TYC) were consistently less favorable than those at our state flagship institutions.
At every school we studied, the overall results deteriorated as the result of one semester of instruction. A significant part of this deterioration was the effort cluster: at every school tested, in their judgments at the end of a semester, students felt that they did not put in as much effort as they had expected to put in at the beginning of the semester. This part of the result is well-known and neither surprising nor particularly disturbing. What is more troublesome is the result that many of the schools showed deteriorations on the cognitive dimensions as well: half deteriorated on the independence dimension, two thirds on the coherence dimension, half on the math link (with the others showing no gain), and all on the reality link.
The workplace and the role of physics in the educational milieu is changing. Modern industry now requires a much larger fraction of its workers to have some technical expertise than was the case thirty years ago, and this trend is likely to continue. Our mandate now is to provide a much larger fraction of our students with successful training in technological thinking skills than ever before.
The small fraction of students who enter our classes with expectations that match the instructors may be identified as "good" students and achieve success with a high probability. Some of these may go on to become physicists. The students who have inappropriate expectations may work extremely hard but still find themselves unable to succeed. Our courses then serve as filters to eliminate those students rather than helping to transform them. Worse yet, some courses may actually reward students with inappropriate attitudes, such as those who prefer memorizing to understanding, while driving away students who might excel in science given a more supportive structure. [34] If we degrade the requirements in our courses so that students can succeed without developing an understanding of the nature of science, the scientific process, or how to learn science and do it, those students who come to college with a mature set of attitudes may survive this approach without damage. But for those who will need to learn and do science at a more advanced level, and who need help with their understanding of what science is and how to think about it, this approach is a recipe for guaranteed failure. [35]
It is inappropriate to respond to the new mandate by "blaming the victim" or claiming that "some students just can't do physics." This is particularly destructive in those cases where students have had previous training in science and math classes that discourages understanding, questioning, and creative thinking. Some students have had great success in courses in this mode over many years in elementary, middle, and high school (and even in college). As has been demonstrated in many areas of cognitive psychology and education research, changing a long-held view is a non-trivial exercise. It may take specifically designed activities and many attempts.
Anecdotal evidence suggests an "existence theorem." Some students who come to college with serious misconceptions about how to do physics make the transition to become excellent students and successful scientists or engineers.
Much of what we do in introductory classes does not address the hidden curriculum of improved understanding and attitudes. Indeed, some of what we do may be counterproductive. If we are to learn the extent to which it is possible to help introductory students transform their approach towards physics, we must observe our students carefully and try to explicate the elements of an appropriate set of expectations.
The failure to begin to move students from a binary view of learning to a more constructivist set of attitudes in the first term of university physics is most unfortunate. The start of college is a striking change for most students. This change of context gives instructors the valuable opportunity to redefine the social contract between students and teachers. This redefinition offers an opportunity to change expectations. If students are told at the beginning of their first college science course: "In high school you may have gotten away with memorizing equations without understanding them, but here that won't be enough" and if that mandate is followed through in both assignments and grading, students are more likely to be willing to put in the effort to change and grow. If students experience a series of science courses that do not require deeper understanding and a growth of sophistication, they will be much more reluctant to put in the time and effort to change in a later course.
The survey presented here is a first step towards exploring these issues and expanding our understanding of what is really going on in our classrooms.
We would like to thank the other members of the University of Maryland Physics Education Research Group, Lei Bao, Michael Wittmann, John Layman, John Lello, and Mel Sabella, who contributed substantially to the collection and analysis of the data presented in this paper. Visitors to the group, including John Christopher, Alvin Sapirstein, and Pratibha Jolly, contributed valuable comments and insights. We are particularly grateful to Lillian McDermott and the members of the University of Washington Physics Education Research Group where this work was begun for their hospitality and valuable discussions when one of us (EFR) was on sabbatical. We would also like to thank the very many faculty members at the institutions involved who cooperated with us and gave us class time for their students to fill out our survey. We are very grateful to Priscilla Laws and her colleagues at the Dickinson College Summer Workshops for agreeing to let us give our survey to workshop participants and to Larry Kirkpatrick and his colleagues for permitting us to survey the USIPOT students. We also would like to thank Priscilla Laws and Edwin Taylor for useful comments about the manuscript.
* Part of this paper is taken from a dissertation to be submitted to the Graduate School, University of Maryland, by Jeffery M. Saul in partial fulfillment of the requirements for the Ph.D. degree in Physics.
| University of Maryland | Physics Department | PERG UMD | The MPEX Project |
|---|---|---|---|
 |
 |
 |
 |