University of Maryland
Computer Tutorials in Physics: Air Resistance

Air Resistance

I. Thinking about motion without air resistance

The program we will use in this session is called AIRRES1. It calculates the motion of a ball in one dimension (up and down) against the force of gravity and a force of air resistance. Before starting the program, answer a few questions about the circumstances described by the program. For the rest of this section, ignore air resistance.

Consider a ball thrown straight upwards.

  1. In the space at the right, sketch a coordinate system for describing a picture of the motion of the ball. Take the starting point to be somewhere near the bottom of the region and make that the origin. Choose the positive x axis to point up. Draw images of the ball after it has left the hand and is part way up, at the top, and part of the way back down.
  2. On your images of each ball draw free-body diagrams indicating all of the forces acting on the ball at that instant of time. For each force, use the notation FB->A that indicates object B is causing the force and object A is feeling it.
  3. The ball is started at time t = 0 with a positive velocity at the origin. In the space below, draw labeled graphs that show the height of the ball as a function of time and the velocity of the ball as a function of time. How do you know they look the way you have drawn them?
  4. When the ball reaches the top of its trajectory, what is its velocity? What forces act on it? What is its acceleration?

II. Familiarizing yourself with the program: Motion without air resistance

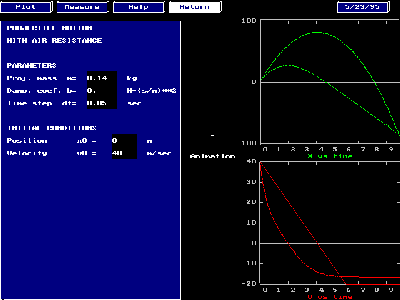
Now start the program. This program solves for and displays the motion of a projectile thrown straight up under the influence of gravity and air resistance. It allows you to choose a variety of different models to describe the air resistance and allows you to change the parameters of the problem (mass, air resistance coefficient, etc.)

To use this program, you will use the menu bars at the top of the screen. The item highlighted in white is the selected item. To change which item is highlighted, use the left and right arrow keys. To activate (carry out the operation of) a selected item, press . We use the term choose to mean select and activate. To find out in detail what each item does, go to the last page of this tutorial.

Right now, select SET DATA and press . You will now see the data-entry screen. The parameters of the problem are shown on this screen. The numbers the program is currently using are shown in the black boxes. You can change any of them by typing over the numbers that are there. Use the arrow keys to change your position on the data-entry screen. For now, just look at the numbers and notice the air resistance is set to zero. Press to accept this data. We will test the accuracy of the program by trying it without air resistance.

Notice that there are now two graphs and an animation. Also notice that the menu has changed. This is the graph menu. The entries are chosen in the same way as those of the main menu, by highlighting them with the arrow keys and pressing . The entries are described in detail the section Program Help at the end of this tutorial.

  1. Choose PLOT to watch the graph again. Do the graphs look like what you expected?
  2. Choose MEASURE to measure the total amount of time the ball takes to rise and fall. Point to the place on the position graph that corresponds to the ball returning to its starting point and click with the left mouse button. The x and t values of the point you clicked on will be displayed at the top of the screen. How close to 0 can you get for the v value? Try a number of times. The uncertainty in this measurement gives you an idea of how accurately you can determine a value from this graph. Write down the total time, Dt, the ball took to rise and fall and your uncertainties in reading x and t which we will call dt and dx. (Use the notation (t ( dt where now (t and dt are both numbers.)
  3. Choose MEASURE and find the time at which the ball reaches the peak. Within your uncertainty, is this one half of Dt?
  4. Choose MEASURE and find the time at which the ball's velocity is zero. What is your uncertainty in the reading of v? Call it dv. Within your uncertainty, does this velocity vanish at the same time the ball reaches its peak?

III. Exploring motion with air resistance

A. Thinking about air resistance
We know that the simple model of forces on falling bodies, W = mg, is really quite limited. The vector g is really only a constant if we assume the earth is flat. It actually points in different directions if you are in different places on the earth. We also have the simple observation that if W were the only force acting on a falling body, then all bodies would fall with the same acceleration.

  1. 1. Assume that we have two bodies with different masses and drop them. If we ignore air resistance, what are the forces acting on the bodies while they are falling?
  2. 2. Write an equation that gives the response of each body to its net force and show that they will have the same accelerations.
  3. 3. In the real world, do all falling bodies have the same acceleration? If not, give a real world example. We might guess that the reason that bodies in the real world do not all fall in the same way is because something else is acting on them other than the earth. Since we know various kinds of touching forces, we might guess that something is touching the objects as they fall -- the air -- and that exerts a force. We'll have to try to make a guess at what that force is.
  4. 4. Would you expect the force that air exerts on an object moving through it to depend on the relative velocity between the object and the air or not? Consider your personal experience with wind.
B. Modeling the force of air resistance
Three models of resistive forces that are often used are:

We will first study the behavior of a ball that is feeling a drag force. (This is the most realistic for objects the size of a ball and it is what the program assumes if you don't change it on the OPTIONS screen.)

1. Choose SET DATA.

Describe how the position and velocity curves change from the case with no air resistance.

Describe what the changes in the curves mean for how the motion of the ball changes from the case with no resistance.

2. You may continue to change the strength of the resistive force by choosing MAIN MENU to get back to the main menu, and SET DATA to get to the data-input screen. You may erase all earlier curves by selecting PLOT from the graph menu.

At these large times is the object accelerating significantly? Use this observation to derive an equation for the value at which the velocity flattens out. This is called the terminal velocity. (Hint: Is the object accelerating if it is falling at terminal velocity? What does that tell you about the net force on it?)

3. When there is air resistance, does the ball take a longer time to go up or to come down?

4. Explain in your own words why it takes longer in one direction than in the other by considering the relative size of the forces on the object as it goes up and as it comes down.

C. The real world -- testing the models

In this part of the tutorial you will need a set of three basket coffee filters and a meter stick. Coffee filters have the nice property that they are light enough and have a large enough area that they reach terminal velocity almost immediately. This means that if you drop one at a distance of a meter it floats down smoothly at essentially a constant speed. This will allow us to determine whether they feel and air resistance force that is approximately proportional to v**2 (Newton drag) or to v (viscous drag).

We will write equations that express the condition that the filter is falling at terminal velocity and rearrange it to derive a simple expression for the time it takes to fall a certain distance. From this, we will be able to see how the time of fall depends on the mass (number of nested filters) and on the distance.

You effectively double the filter's mass without changing the air resistance it feels by nesting two filters inside each other. Since only one of them is pushing its way through the air, the air resistance force doesn't change.

  1. Can you find a new distance, D, so that the time it takes the double filter to fall D is the same as the time it takes a single filter to fall a distance S?
  2. Take S to be 1 meter. Drop two filters one nested inside each other from the height D at the same time as you drop a single filter from the height S. Do they hit at the same time?
  3. Repeat the argument assuming quadratic drag, F = bv**2. Now what should D be compared to S? It you use these distances, now do they hit at the same time?

Program Help

The menu items on the menu you see first (the main menu) do the following things:

Choose SET DATA. You will now see the data-entry screen. The parameters of the problem are shown on this screen. The numbers the program is currently using are shown in the black boxes. You can change any of them by typing over the numbers that are there. Use the arrow keys to change your position on the data-entry screen. For now, just look at the numbers. Press to accept this data.

Notice that there are now two graphs and an animation. Also notice that the menu has changed. This is the graph menu. The entries are chosen in the same way as those of the main menu, by highlighting them with the arrow keys and pressing . The entries do the following things:

Some Links:
The M.U.P.P.E.T. Utilities is available from Physics Academic Software (phone 1-800-955-TASL for information or orders).

Edward F. Redish
Jack M. Wilson
Ian D. Johnston

Information about PERG Resource materials from PERG PERG Homepage PER elsewhere on the web Resource materials for teachers
This page prepared 22. May 1995 by
Edward F. Redish
Department of Physics
University of Maryland
College Park, MD 20742
Phone: (301) 405-6120
Email: redish@quark.umd.edu