1) For each of the following partial sentences, indicate whether they
are correctly completed by the symbol corresponding to the phrase greater
than (>), less than (<), or the same as (=).
(a) A chunk of iron is sitting on a table. It is then moved from the table
into a bucket of water sitting on the table. The iron now rests on the
bottom of the bucket. The force the bucket exerts on the block when the
block is sitting on the bottom of the bucket is __________the force that
the table exerted on the block when the block was sitting on the table.
(b) A chunk of iron is sitting on a table. It is then moved from the table
into a bucket of water sitting on the table. The iron now rests on the
bottom of the bucket. The total force on the block when it is sitting on
the bottom of the bucket __________ it was on the table.
(c) A chunk of iron is sitting on a table. It is then covered by a bell
jar which has a nozzle connected to a vacuum pump. The air is extracted
from the bell jar The force the table exerts on the block when the block
is sitting in a vacuum is __________the force that the table exerted on
the block when the block was sitting in the air.
(d) A chunk of iron is sitting on a scale. The iron and the scale are then
both immersed in a large vat of water. After being immersed in the water,
the scale reading will be __________the scale reading when they were simply
sitting in the air. (Assume the scale would read zero if nothing were sitting
on it, even when it is under water.)
| 2) You and your friends are sitting in an open meadow on
a summer day having a picnic. You look up and notice a hot air balloon
floating toward you. The balloon is approximately a sphere with a radius
of 6 meters and is drifting directly towards you at a speed of about 10
m/s. Hint: The density of normal air is about 1 kg/m3 and the speed of
sound in normal air is about 333 m/s (= 1000/3).
(a) You guess that the density of the air inside the balloon is 1/2
the density of the air outside the balloon. If that is so, how much does
the balloon plus its gondola weigh? (Hint: The density of normal air is
about 1 kg/m3.)
(b) As the balloon gets closer, you notice that music is coming from a
CD player in the balloon's gondola -- Mariah Carey is holding a high note.
Your friend who has perfect pitch thought he remembered that it was a C
(512 Hz) but he says it sounds a bit off. Why? If the CD is playing a C,
what frequency do you hear? Explain.
|
 |
3) Explain why a helium balloon in a closed automobile moves to the
front of the car when the car accelerates, whereas the passengers feel
pushed backwards.
4) Suppose you have the following collection of objects: * a pencil,
* a coin, * an empty plastic box for cassette tapes with its edges taped
shut, * the same box opened up, * a needle, * an unopened can of soda pop,
and * an empty can of soda pop. Which of these objects do you expect will
float and which will sink on water? Will it make a difference if you carefully
place the object with its largest surface on the surface of the water?
In which cases? Explain your reasoning. After you have written your answer,
perform the experiments and compare your results with your predictions.
5) The density of water is just about 1000 kg/m3. The density of air
is just about 1000 times less -- 1 kg/m3 (actually 1.3 kg/m3 at sea level.)
From your knowledge of the air pressure at ground level, estimate the height
of the atmosphere. As a simplifying assumption, take the atmosphere to
be of uniform density up to some height after which the density rapidly
falls to zero. (In reality, the density of the atmosphere decreases as
we go up.)
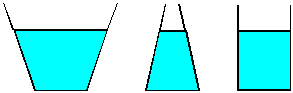
| 6) Water is poured to the same level in each of the three
vessels shown. Each vessel has the same base area. Since the water is to
the same depth in each vessel, each will have the same pressure at the
bottom. Since the area and pressure is the same, each liquid should exert
the same force on the base of the vessel. Yet, if the vessels are weighed,
three different values are obtained. (The one in the center clearly holds
less liquid than the one at the left, so it will weigh less.) How can you
justify this apparent contradiction? |
 |
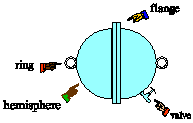
| 7) In 1654, Otto von Guericke, burgomeister of Magdeburg
and inventor of the air pump, gave a demonstration in which two teams of
eight horses could not pull apart two brass hemispheres held together only
by the pressure of the outside air. The sphere was about the size of a
basketball. Estimate the force the teams of horses would have had to exert
to pull the hemispheres apart. |
 |
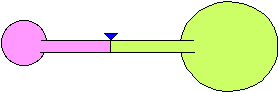
8) Two balloons are blown up to different sizes and connected to the
opposite sides of a hollow tube. The tube has a valve to prevent air from
going from one balloon to the other. The balloons are of different sizes
as shown in the figure. When the valve is opened, what will happen? Explain
your reasoning.
(a) The larger balloon will get smaller and the smaller balloon will
get larger until they are of equal size.
(b) The smaller balloon will get smaller and the larger balloon will get
larger until the smaller balloon is almost gone.
(c) Nothing will happen. They will stay the same size.
|
 |
9) An ideal gas is contained in an airtight box. Complete each of the
following five statements below to show the quantitative change that will
occur. For example, if you want to say that the volume, initially equal
to V, quadruples, complete the statement with "4V".
(a) If the absolute temperature of the gas is halved, the average speed
of a gas molecule, v0, becomes _____.
(b) If the average speed of a gas molecule doubles, the pressure, p, on
a the wall of the box becomes _____.
(c) If the absolute temperature of the gas is halved, the pressure, p,
on a wall of the box becomes _____.
(d) If the absolute temperature of the gas is increased by 25%, the total
internal energy of the gas, U, becomes _____.
(e) If the number of gas molecules inside the box is doubled, but the temperature
is kept the same, the pressure, p, on the wall of the box becomes _____.
10) The actual diameter of an atom is about 1 Angstrom (10-10
m). In order to develop some intuition for the molecular scale of a gas,
assume that you are considering a liter of air (mostly N2 and
O2) at room temperature and a pressure of 105 Pa.
(a) Calculate the number of molecules in the sample of gas.
(b) Estimate the average spacing between the molecules.
(c) Estimate the average speed of a molecule using the Maxwell-Boltzmann
distribution.
(d) Suppose that the gas were rescaled upwards so that each atom was the
size of a tennis ball (but we don't change the time scale). What would
be the average spacing between molecules and the average speed of the molecules
in miles/hour?
11) A good student makes the following observation. "If I try to
accelerate a small sphere through air, it will be resisted by the air.
If I drop an object, it will eventually reach a terminal velocity where
the air is resisting as much as gravity is trying to accelerate. The smaller
the ball the slower the terminal velocity. But you tell me the Maxwell
distribution says that the molecules of air move very rapidly. I estimate
that this is much faster than the molecule's terminal velocity, so it can't
move that fast. The Maxwell distribution must be wrong."
(a) The Newton drag law for a sphere moving through air is calculated
by a molecular model to be |Fair res| = 2¼rR2v2
where R is the radius of the sphere, r is the
density of the air, and v is the velocity of the object through the air.
Calculate the terminal velocity for a sphere the size and mass of an air
molecule falling through a fluid the density of air (r
= 1 kg/m3).
(b) From your estimate in the previous problem, is this speed greater or
less than the average speed the molecule should have given the M-B distribution?
What is wrong with the student's argument?
12) For each of the following partial sentences, indicate whether they
are correctly completed by the word or phrase is greater than (>), is
less than (<), or is the same as (=).
(a) An air bubble formed at the bottom of a pan of water increases in
size as it rises towards the top surface of the water. As the bubble goes
up, the pressure inside the bubble __________ it was on the bottom.
(b) A block of iron is sitting on a table. It is then moved from the table
into a bucket of water sitting on the table. The iron now rests on the
bottom of the bucket. The total force on the block when it is sitting on
the bottom of the bucket __________ it was on the table.
(c) A cube of ice at 0 °C is floating in a dish of water at 0 °C.
The internal energy for one gram of the ice __________ the internal energy
for one gram of the water.
(d) In a liter of hydrogen (mass = 2 amu) at STP, the number of molecules
is __________ the number of molecules in a liter of oxygen (mass = 32 amu)
at STP.
(e) In a sample of gas containing hydrogen and oxygen at room temperature,
the average velocity of a hydrogen molecule (mass = 2 amu) is __________
the average velocity of an oxygen molecule (mass = 32 amu).
13) Why does Avogadro's hypothesis (that a given volume of gas at a
given temperature and pressure has the same number of molecules no matter
what kind of gas it is) not hold for liquids and solids?
14) Imagine, as some scientists did in the eighteenth century, that
the molecules of a gas occupy fixed positions and are in contact with each
other. What conclusions about molecular diameters could you draw (a) from
the law of combining volumes and Avogadro's hypothesis and (b) from the
ideal gas law?






![]()