1) The polar ice caps contain about 2.3 x 1019 kg of ice.
This mass contributes essentially nothing to the moment of inertia of the
earth because it is located at the poles, close to the axis of rotation.
Estimate the change in the length of the day that would be expected if
the polar ice caps were to melt and the water were distributed uniformly
over the surface of the earth.
(Hint: The moment of inertia of a thin spherical shell of radius
r and mass m is (2/3)mr2.)
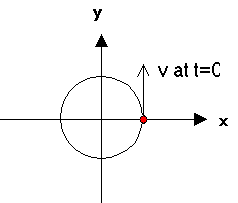
| 2) An object is clipped to the edge of a disk that is rotating with uniform
circular motion. At time t=0 it is at the position shown and it has the
velocity shown. It travels around with the disk for a full rotation. A
series of graphs is shown below. Identify which of these graphs could represent
the following six items (if it had the appropriate scales):
(a). The x component of the object's velocity.
(b) The angle the object's position makes with the x axis.
(c) The y component of the force keeping the object moving in a circle.
(d) The object's angular velocity.
(e) The object's speed.
(f) The x component of the object's position.
|
 |
3) In the figure below are shown snapshots of four situations in which
a set of 4 point masses are moving in various configurations.
The masses are all identical and each has a mass m. Their speeds
are all identical and have the value v, and each mass is a distance
R from the place where the dotted lines cross (the system origin).
The arrows indicate the direction of motion of the masses at the instant
the snapshot was taken. Where a thin ring is shown, the masses are attached
to a light (nearly massless) plastic hoop.
Use the coordinate directions shown on the right but for each system
take the origin to be at the indicated crossing of the dotted lines.

Calculate the values of the total linear momentum and total energy of
motion for each case. (Be sure to include an indicator of the direction
where appropriate.)
| 4) In the movie Jurassic Park, there is a scene in which some members
of the visiting group are trapped in the kitchen with dinosaurs outside
of the door. The paleontologist is pressing against the center of the door,
trying to keep out the dinosaurs who are on the other side. The botanist
throws herself against the door at the edge right next to the hinge. A
pivotal point in the film is that she cannot reach a gun on the floor because
she is trying to help hold the door closed.
If the paleontologist is pressing at the center of the door, and the
botanist at the edge by the hinge, estimate how far the paleontologist
would have to relocate in order to have a greater effect on keeping the
door closed than both of them pushing together have in their positions
as shown in the film.
|
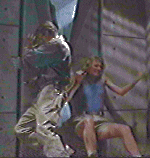 |
5) You are standing on the ground and an airplane flies towards you
at a speed of 300 km/hr at a height of 1000 m above the ground. It passes
right above you. The airplane has a mass of 50,000 kg.
(a) Calculate the airplane's angular momentum with respect to you at
the moment it passes above your head.
(b) Explain why the airplane has an angular momentum even though it is
traveling in a straight line. Note: Your answer must make the idea
plausible. It is not enough to state a formula.
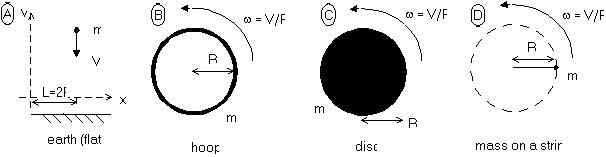
6) The four objects in the figures below are moving as indicated by
the arrows. A curved arrow indicates a rotation about the center. For object
(A) use the coordinates shown. For the others, take the origin at the center
of the circle. Use the directions associated with the coordinate axes shown
at the right. Construct table with the values of
- the total linear momentum,
- total angular momentum, and
- total energy of motion
at the instant shown for each case. Express your answers in terms of
m, V, and R. (Include an indicator of the direction where appropriate.)
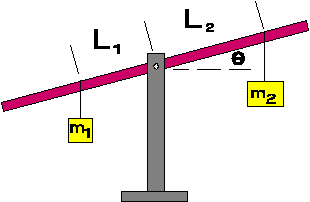
| 7) A straight rod of negligible mass is mounted on a frictionless pivot
as shown in the figure at the right. Masses m1 and m2
are suspended at distances L1 and L2 as shown.
(a) Write an expression for the potential energy of the masses as a
function of the angle q made by the rod and
the horizontal.
(b) For what angle q is the potential energy
a minimum? Is the statement "systems tend to move towards minimum
potential energy" consistent with your result?
(c) Show that if m1L1 = m2L2,
the potential energy is the same for all values of q.
When this holds, the system will balance at any angle q.
This result is known as Archimedes' Law of the lever.
|
|
8) When preparing to travel to Australia last summer, I was concerned
that my suitcase was too heavy. (There is a 20 kg limit on suitcases for
international travel). Unfortunately, I only had a small bathroom scale.
I tried standing on the scale, measuring my weight, and then standing on
the scale holding the suitcase. Unfortunately, when I was holding the suitcase,
I couldn't see the markings on the scale, and it was too heavy to hold
behind me. Design a way for me to measure the weight of my suitcase.
9) Estimate the angular momentum your body has as a result of the earth's
daily rotation about its north-south axis.
| Two masses, M1 and M2, are connected by a string
which runs over a pulley as shown in the figure below. Assume the pulley
has a mass m and a radius R and that there is no friction between the surface
of the inclined plane and the mass M2.
(a) Draw free-body diagrams for the forces on masses M1 and
M2, being sure to specify the agents responsible for each force.
(b) Consider the two masses, the cord, and the pulley as a system. Find
the net external torque acting on this system about the center of the pulley.
(c) Write an expression for the total angular momentum of the system about
the center of the pulley assuming the masses are moving with an instantaneous
velocity v. Assume the pulley is a flat disk of mass m, and that the string
does not slip so that a point on the surface of the pulley is also moving
with an instantaneous velocity v.
(d) How is the angular velocity of the pulley related to the velocity of
the masses?
(e) Find the acceleration of the masses.
|

|
| 10) A flywheel with a mass M and radius R is positioned
to sit horizontally and rotate on a vertical axis. The rim of the wheel
is wrapped with a cord that lets you start it spinning by pulling on it.
If you pull on it until the cord unwraps completely using a constant force
F, and if the cord has a length d, find the final angular
momentum of the wheel when you are finished pulling. |
 |
11) Estimate the angular momentum an automobile tire has about its axis
of rotation while the car is driving on the beltway.
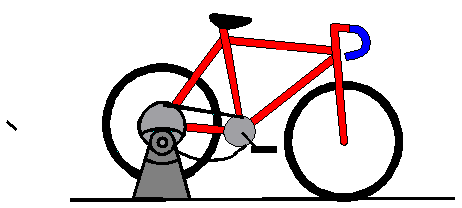
| 12) A bicycle wheel is held off the ground by a rigid stand and is
driven by a chain pulling a sprocket gear as shown in the figure. Only
the top side of the chain is taut; the bottom is slack. The mass of the
wheel is M and the mass of the sprocket is m << M.
The wheel has a radius R and the sprocket has a radius r.
(a) If I crank the pedals so that the tension in the chain is T,
what will be the angular acceleration, a, of
the wheel?
(b) Starting from rest, how long a time, t, will I have to crank
to get it up to an angular velocity of w? (Ignore
friction in the bearings.)
>(c) If the values of the parameters are M = 2 kg, R =
0.7 m, r = 0.15 m, T = 20 N, and w
= 200 revolutions/minute, find the values of a
and t.
|
 |
13) Estimate the angular momentum of the earth due to its daily rotation
about its axis. The average density of the earth is about 5 grams/cm3.
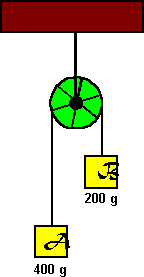
| 14) In the figure at the right is shown an Atwood's machine with two
unequal masses attached by a massless string. The pulley has a mass of
20 g and a radius of 2 cm.
(a) State three approximations that you can make to simplify your calculation
of the motion of the blocks. ("Making an approximation" is the
process of ignoring a physical effect because you expect it to be small
and have little effect on your result is you only want a few significant
figures. If you want more, you may have to include those effects.)
(b) Using your approximations, find the acceleration of block A.
(c) What happens to your result if the two masses are equal. Is the result
what you expect? Explain.
(c) If you have suppressed the moment of inertia of the pulley in your
calculation in the second part of this problem, set up the equations that
would allow you to solve for the acceleration when it is included.
|
 |
| 15) In testing a design for a yo-yo, an engineer begins by constructing
a simple prototype -- a string wound about the rim of a wooden disk. She
puts an axle riding on nearly frictionless ball bearings through the axis
of the wooden disk and fixes the ends of the axle. In order to measure
the moment of inertia of the disk, she attaches a weight of mass m
to the string and measures how long it takes to fall a given distance.
(a) Assuming the moment of inertia of the disk is given by I,
and the radius of the disk is R, find the time for the mass to fall
a distance h starting from rest.
(b) She doesn't have a very accurate stopwatch but wants to get a measurement
good to a few percent. She decides a fall time of 2 seconds would work.
How big a mass should she use? Imagine you were setting up this experiment
and make reasonable estimates of the parameters you need.
|
 |
16) One proposal for reducing air pollution is the flywheel-driven automobile.
Instead of an engine, the car contains a large steel disk, or flywheel,
which is mounted to rotate about a vertical axis. It is set spinning at
a high angular velocity in the early morning using electric power (from
plugging it into the wall). If the car is to be about the same size as
a typical car today, estimate the amount of energy that could be stored
in a rotating steel flywheel that fits under the car's hood. You may find
some of the following numbers useful:
density of steel = 6 gm/cm3
mass of a typical car = 1000 kg
maximum speed of flywheel = 1000 revolutions/minute
fraction of carbon monoxide pollution produced by vehicles = 60%.
17) Two students are driving a Porsche of mass M at a constant
speed v around the traffic circle in front of the Physics building.
Assume that the road in the circle is level and has a radius R.
The coefficient of friction between the car's wheels and the road is m.
(a) In terms of the quantities given, what is the magnitude and direction
of the car's acceleration?
(b) At the instant when it passes directly in front of the Physics building,
is there a net force on the car? If there is, what is responsible for it
and how big must it be? Express your answer in terms of the quantities
given and explain your reasoning.
(c) The mass of the car and passengers is 1700 kg, the circle has a radius
R = 25 m, and the coefficient of friction between rubber
and a dry road is m = 0.6. What is the
fastest speed the car can go without slipping?
|
 |
18) A new low pollution automobile might run on energy stored in a spinning
disk, or flywheel. The wheel would be set spinning in the morning
(using electrical energy from a plug in the wall) and its energy drawn
off a bit at a time to set the car moving. For this problem, we will ignore
the mechanisms required for getting the flywheel spinning and for transferring
the flywheel's energy to the wheels of the car. We will simply calculate
the energies required.
(a) Suppose the car had a loaded mass of 2000 kg (including the mass
of the flywheel and passengers). How much energy in Joules do we need to
provide to get the car up to a speed of 15 m/s (about 33 mph)?
(b) Suppose the flywheel was a solid steel disk with a radius of 40 cm
and a height of 25 cm. The density of steel is 6 gm/cm3. Calculate
its moment of inertia.
(c) If we wanted the flywheel to contain enough energy to bring the car
up to speed 100 times during the day, how fast would it have to be spinning
when we left in the morning?
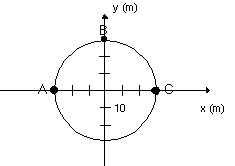
| 19) A jogger runs around a circular track of 30 m radius at a
constant speed in a clockwise direction. He completes one lap in 40 seconds.
(a) Compare the directions and magnitudes of
(1) his instantaneous velocity at A,
(2) his instantaneous velocity at C, and
(3) his average velocity going from A to C.
(b) If the runner completes exactly one lap what is his average velocity?
Explain your answer.
(c) Is the magnitude of his average velocity from A to B bigger, smaller
or equal to the magnitude of his average velocity from A to C? Explain
your reasoning.
|
 |
20) A refrigerator has separate shelves on the door for
storing bottles as shown in the picture at the right. Thin plastic straps
keep the bottles from falling of the door. At one point, a teenager under
the influence of too much teenage energy and hormones, slammed the door
with a bit too much vigor and a heavy bottle broke the strap.
- Do you think the bottle would be more likely to break the plastic strap
if it is close to the hinge? close to the handle? or doesn't it matter?
- Explain your answer in terms of the physics we have learned.
|
 |
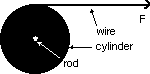
| 21) Wire is often delivered wrapped on a large cylindrical spool. Suppose
such a spool is supported by resting on a horizontal metal rod that is
pushed through a hole that runs through the center of the spool. A worker
is pulling some wire off the spool by exerting a force on it something
like is shown in the diagram at the right. (If you have ever bought wire
in a hardware store, this is the way they usually store and dispense it.)
Suppose the spool rotates on the rod essentially without friction. The
spool is approximately a uniform cylinder with a mass of 50 kg and a radius
of 30 cm. The worker pulls on the wire for 2 seconds with a force of 30
Newtons. At the end of the 2 seconds he immediately clamps on a brake which
very quickly stops the spool's rotation. Just before he put the brake on,
how fast was the spool rotating? How much wire did he pull off the spool?
|
 |
















![]()