Teaching Physics with the Physics Suite Edward F. Redish Home | Action Research Kit| Sample Problems | Resources | Product Information
	Problems Sorted by Type | Problems Sorted by Subject | Problems Sorted by Chapter in UP

A superball is dropped from a height of 1 m and bounces a number of times before it is caught. Below are shown graphs of some of the physical variables of the problem. Match the graphs that best show the time dependence of the variables in the list below the graphs. (Assume for these first few bounces the superball can be treated as a “perfect bouncer.”)

You may use a graph more than once or not at all. If none of the graphs work well for a variable, put N. Note: the time axes are to the same scale, but the ordinates {"y axes"} are not.

The time t = 0 is taken to be the instant when the ball leaves the hand. Use a coordinate system in which the positive direction is taken as up and the origin is at the floor.

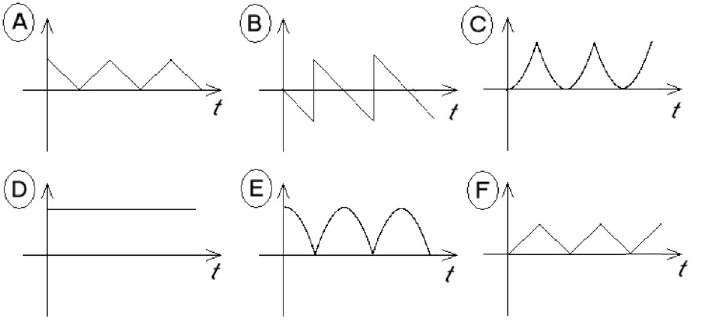
a. The velocity of the ball
b. The kinetic energy of the ball
c. The potential energy of the ball
d. The momentum of the ball
e. The total mechanical energy of the ball.
f. The position (y coordinate) of the ball

Page last modified November 5, 2010: PE33