Teaching Physics with the Physics Suite Edward F. Redish
	Problems Sorted by Type | Problems Sorted by Subject | Problems Sorted by Chapter in UP

The interference of X-rays is a method for studying the properties of crystals. It has been extremely valuable in biology, helping to clarify the structure of many critical molecules, including DNA. (Rosalind Franklin’s work using this technique played a critical role in helping Crick and Watson figure out the double helix.) The way this works is that the crystal sample has its molecules in a regular pattern. When an x-ray beam hits it, each pair (and more) of molecules scatters the x-rays, serving as sources of outgoing spherical waves – like the slits in our interference experiment. Depending on the layout of molecules in the crystal, we get constructive interference spots at various places on the screen. With some appropriate math, the arrangement of the molecules in the crystal can be read off from the pattern of spots. Let’s get an idea of what the scales are by considering a simple example. Suppose we have a crystal in which all the molecules are equally and regularly spaced as shown in the magnifying glass at the right. Although we could choose any pair of atoms, we have picked two particular ones, shown in darker color. Let us only consider the x-rays scattered from these two atoms.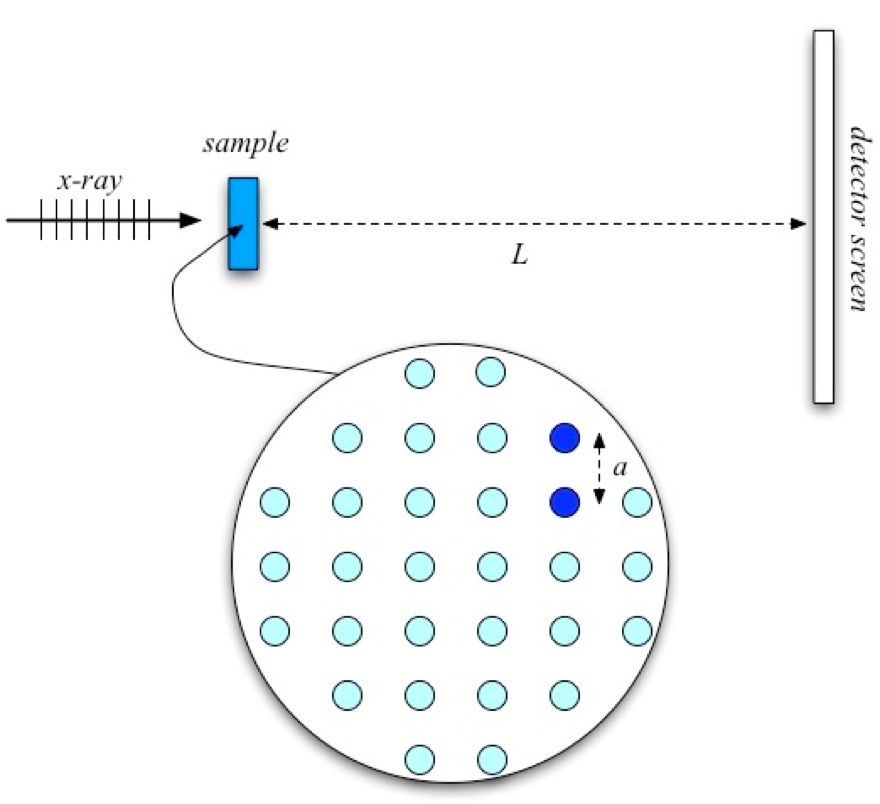

(a) Suppose the atoms are a distance a apart, the detector screen is a distance L from the sample, and the x-rays have a wavelength λ. The pattern produced by this pair is a central bright spot with a string of beadlike spots, separated from each other by a distance Δy. Construct an equation that will allow you to find the separation of the atoms, a, from your measurements of L and Δy and from the wavelength of the x-ray (written on the x-ray source). Explain your reasoning.

(b) A typical wavelength for an x-ray is 1 nanometer (10^-9 m). If your detector is 40 cm from the sample and the spot separation is 15 cm, find the spacing between the atoms.

Page last modified April 26, 2012: OP26