Teaching Physics with the Physics Suite Edward F. Redish Home | Action Research Kit| Sample Problems | Resources | Product Information
	Problems Sorted by Type | Problems Sorted by Subject | Problems Sorted by Chapter in UP

We can make the observation that we can hear around corners (somewhat) but not see around corners. Estimate why this is so by considering a doorway and two kinds of waves passing through it. A beam of red light (λ = 660 nm) A sound wave playing an "A" (f = 440 Hz). Treat these two waves as plane waves passing through a slit whose width equals the width of the door. Find the angle that gives the position of the first dark diffraction fringe. From that, assuming you are 2 m back from the door, estimate how far outside the door you could be and still detect the wave. (See the picture for a clarification. The distance x is desired.)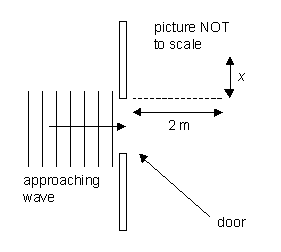

Note: The speed of light in air is about 3 x 10⁸ m/s and the speed of sound in air is about 330 m/s.

Not finding what you wanted? Check the Site Map for more information.

Page last modified October 31, 2002: OP16