
Teaching Physics with the Physics Suite
Edward F. Redish
Home | Action Research Kit| Sample Problems | Resources | Product Information
Problems Sorted by Type | Problems Sorted by Subject | Problems Sorted by Chapter in UP
 |
Teaching Physics with the Physics Suite Edward F. Redish Home | Action Research Kit| Sample Problems | Resources | Product Information |
Problems Sorted by Type | Problems Sorted by Subject | Problems Sorted by Chapter in UP |
Take four little coffee stirrer straws. Connect them with Scoth tape in the two different configurations as shown in the figure at the right: two of them in parallel (side by side - the left configuration), and two of them in series (end to end - the right configuration). Blow through each configuration, blowing as hard as you can until you empty your lungs. You should find that using one of the combinations allows you to empty your lungs more quickly than the other. Measure the time each takes. Let's figure out exactly how the resistance of each straw adds in order to produce a combined or total resistance for each configuration in order to get a theoretical prediction of how the flow compares in the two cases. The basic tool we need is the Hagen-Poiseuille equation that relates the pressure drop across the ends of a pipe with the volume current flowing through it: Δp = JZ, where Δp is the pressure difference across the ends of the pipe, J is the volume flowing through the straw per second, and Z is the resistance of the straw. |
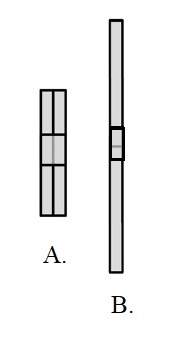 |
If each individual straw has an identical resistance Z, find the effective resistance of the two combinations A and B.
Do this by construct an H-P equation for the combination. You will need to figure out what the pressure drop is across the combined straws, and what the current flow is through the combined straws. This will give an effective resistance for each combination,
Zeff = Δp/J.
where in this equation, Δp and J are the pressure drop and flow for the combination.
Your result for the two combinations should allow you to predict the ratio of the times it takes to empty your lungs in the two cases. How well does the prediction of the flow rate agree with the times you measured?
(Problem by H. Dobbins and E. Redish)
Page last modified November 26, 2008: M23