
Teaching Physics with the Physics Suite
Edward F. Redish
Home | Action Research Kit| Sample Problems | Resources | Product Information
Problems Sorted by Type | Problems Sorted by Subject | Problems Sorted by Chapter in UP
 |
Teaching Physics with the Physics Suite Edward F. Redish Home | Action Research Kit| Sample Problems | Resources | Product Information |
Problems Sorted by Type | Problems Sorted by Subject | Problems Sorted by Chapter in UP |
In this problem we consider what controls how much fluid is flowing through a pipe. The argument is set up here apply to water in the pipes in your house, but it could also be written in a similar way for blood in your arteries, or electrons in a wire. Our goal is to derive an equation relating the amount of fluid flowing in the pipe (current = I = mass/sec) and the pressure differential (ΔP) driving the mass through the resisting pipe.
Consider a fluid (of density ρ) completely filling a straight pipe (with circular cross section and radius r) and flowing through at a constant speed v. We will assume there is a drag force between the fluid and the wall that tries to slow the fluid down. A reasonable model for this force is that it is proportional to the area of contact between the fluid and the wall and to the speed of the fluid relative to the wall:
Drag force / unit length of pipe = - cv.
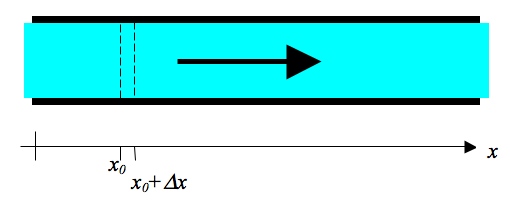
(a) How much fluid is entering (and leaving) the pipe per second? Express your answer in terms of the symbols we have defined so far. In order to figure out what is happening, let's consider a small slice of the fluid, the bit between coordinates x0 and x0 + Δx. This is shown by the dotted lines in the figure below.
(b) For this small bit of fluid moving with a velocity v, let's find some properties.
(c) In order to maintain the fluid moving at a constant speed, the pressure must change along the pipe. Explain why. (Hint: If the pressure were constant throughout the pipe, what would the force balance on the bit of fluid be and what would its motion be (qualitatively)?)
(d) Suppose the pressure along the pipe varies as a function of x by some (unknown) function, P(x). Find an expression for the change in pressure in terms of the symbols we have specified so far.
(e) Show that the linear function P(x) = Ax + B satisfies that change equation you obtained in (d) if you choose A correctly. Can you determine B from what you got in equation (d)? If so, do it. If you can't, explain why not.
(f) For a pipe of length L, use your results from (e) to show that the flow of matter through the pipe (I) is related to the pressure drop across the pipe [ΔP = P(L) - P(0)] by an equation of the form ΔP = IR. where R is the resistance of the pipe (not the radius). You should get that R is some messy combination of the parameters of the problem (L, r, c, ?, etc.). Discuss the dependence of R on these parameters and whether your result for the various dependences of R is plausible (i.e., is it bigger or smaller for a longer pipe? Is that reasonable? etc.)
Not finding what you wanted? Check the Site Map for more information.
Page last modified August 3, 2008: M21