Teaching Physics with the Physics Suite

Edward F. Redish

Home | Action Research Kit| Sample Problems | Resources | Product Information

Problems Sorted by Type | Problems Sorted by Subject | Problems Sorted by Chapter in UP

Charge on a neuron

A neuron is a body cell that functions to create and transmit electrical signals. To do this, it uses chemical processes to maintain an electrical potential difference across its cell membrane. In this problem we will use our knowledge of electrical relationships to estimate the amount of charge on the membrane. Neurons come in a range of sizes, but a typical one may have a cell body of 20 μm (2 x 10-5 m) across. The thickness of the membrane is the same for most neurons – about 5 nm (5 x 10-9 m). The potential difference across a resting nerve membrane is about 70 mV (70 x 10-3 V). We’ll model a piece of the cell membrane 10 μm x 10 μm across as a pair of infinite parallel plates separated by a distance d = 5 nm, with one plate representing the inner edge of the membrane and the other representing the outer edge of the membrane. 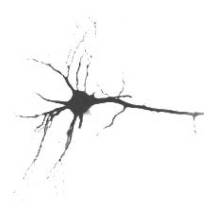neuron
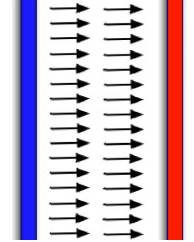parallel plates

A. Assuming the space separating the two plates of our membrane is empty space, calculate the electric field between the plates.

B. Using the electric field you found in part A, calculate the charge density, σ (charge per unit area), on the plates. (Hint: The E field near to a single plate of charge having a uniform charge density σ, is 2πkCσ where kC = 9 x 109 N-m2/C2.)

C. Using the charge density you found in B, calculate the magnitude of the charge on each side of the piece of cell membrane we are modeling and the net charge on the piece of the membrane.

D. Do you think our model of the electric fields and potentials in a cell membrane as infinite parallel plates is a good one? Give reasons for your judgment.

Page last modified April 4, 2009: E57