
Teaching Physics with the Physics Suite
Edward F. Redish Home | Action Research Kit| Sample Problems | Resources | Product Information
Problems Sorted by Type | Problems Sorted by Subject | Problems Sorted by Chapter in UP
 |
Teaching Physics with the Physics Suite
Edward F. Redish Home | Action Research Kit| Sample Problems | Resources | Product Information |
Problems Sorted by Type | Problems Sorted by Subject | Problems Sorted by Chapter in UP |
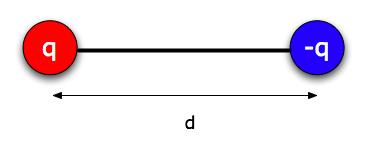
Lots of things that are electrically neutral overall have one side that's electrically negative and one side positive (a water molecule, for example). We call such things "electric dipoles," and we can model them as pairs of particles of charge + q and -q (where q is a positive number) separated by a distance d. Usually, d is a very small distance. (For water it would be around 10-11 m, thinking of a few protons worth of charge on one end - about 6 x 10-19 C -- and a few electrons worth at the other.) Furthermore, because of the magic of quantum mechanics, in many molecules it behaves more like a rigid rod than like a soft spring. So we can treat d as a fixed distance.*
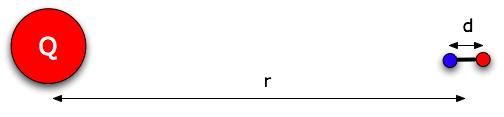
Suppose you have a dipole that's free to move in any way (including rotate - imagine it floating in space). And there's an object with charge Q a distance r away. That distance r would be much larger than d, the distance between the charges of the dipole, so we draw the dipole small.

a) Consider the forces between the charge Q and the dipole. If the dipole is free to rotate:
b) Since water molecules are dipoles, you can test your idea: Rub some wool or flannel on a hard rubber comb to get a charge on it, and then hold it near a thin stream of water coming from a faucet. What happens?
Think of the dipole as lined up the way it's drawn below, so the -q end is a distance r from Q , and the + q end is a distance r + d.
c) Write a formula for the total force on the dipole by the charge Q.
d) If you were to double the distance r between Q and the dipole, what would happen to the magnitude of the force? Would it double? Cut in half? Something else?
You could work on this in a couple of ways; pick whichever one you prefer. One way would be to try numbers. You could use the water molecule if you like, q = 6 x 10-19 C and d = 10-11 m. A reasonable amount of charge for Q might be 10-6 Coulombs, and r could be 1/2 cm = 5 x 10-3 m. Find F, and then double r. Or you could make up your own numbers - you could pick easier numbers - just be sure d is much smaller than r.
The other, more advanced way is to simplify the formula you found in part c). A trick to make that easier is to ignore the term d 2 you'll get along the way. Remember that d is a very small number compared to r, and so d2 is a very very small number compared to r2. When you're adding numbers, and you know one is tiny compared to the others, you can often ignore it. (As in 1,000,000 + 2 is about equal to 1,000,000.) So - at one point you'll have ( r2 + 2rd + d2), and you can ignore the d2 - just cross it out. (Don't ignore the 2rd though! Why not?)
* Water doesn't actually look like a pair of charges separated by a distance. It's more like a pair of "Mickey Mouse ears" with the oxygen atom being the head and the hydrogen atoms being the ears. The hydrogen atoms have excess positive charge and the oxygen has excess negative charge. It turns out that the difference between a "two-ball-and-stick" dipole and "Mickey Mouse ears" becomes irrelevant to the electric field or forces calculated once the distance to the molecule is more than a few molecular diameters.
Problem by D. Hammer
Not finding what you wanted? Check the Site Map for more information.
Page last modified Apri; 2, 2009: E26