
Teaching Physics with the Physics Suite
Home | Action Research Kit| Sample Problems | Resources | Product Information
Problems Sorted by Type | Problems Sorted by Subject | Problems Sorted by Chapter in UP
 |
Teaching Physics with the Physics Suite
Home | Action Research Kit| Sample Problems | Resources | Product Information |
Problems Sorted by Type | Problems Sorted by Subject | Problems Sorted by Chapter in UP |
Gauss's law is usually written as an equation in the form
A long thin cylindrical shell of length L and radius R with L>>R is uniformly covered with a charge Q. If we look for the field near to the cylinder somewhere about the middle, we can treat the cylinder as if it were an infinitely long cylinder. Using this assumption, we can calculate the magnitude and direction of the field at a point a distance d from the axis of the cylinder (outside the cylindrical shell, i.e., L>>d > R but d not very close to R) using Gauss's Law. Do so by explicitly following the steps below.
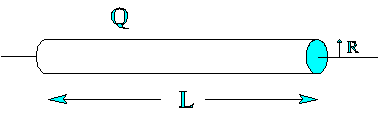
Not finding what you wanted? Check the Site Map for more information.
Page last modified October 31, 2002: E19