Problems for
Intermediate Methods in Theoretical Physics

Edward F. Redish

Ohm's law in a pipe

In this problem we consider what controls how much fluid is flowing through a pipe. This kind of argument is set up here apply to water in the pipes in your house, but it could also be written in a similar way for blood in your arteries, or electrons in a wire. Our goal is to derive an equation relating the amount of fluid flowing in the pipe (current = I = mass/sec) and the pressure differential (Δp) driving the mass through the resisting pipe.

Consider a fluid (of density ρ) completely filling a straight pipe (with circular cross section and radius r) and flowing through at a constant speed v. The simplest approximate model for this is to assume there is a drag force between the fluid and the wall that tries to slow the fluid down. A reasonable model for this force is that it is proportional to the area of contact between the fluid and the wall and to the speed of the fluid relative to the wall: Drag force / unit area of wall-fluid contact = - cv. (This is not how it actually works, but it's a reasonable first try.)

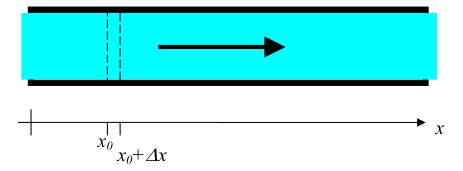
(a) How much fluid is entering (and leaving) the pipe per second? Express your answer in terms of the symbols we have defined so far. [We label the quantity of matter (in kg/s) entering the pipe I.] In order to figure out what is happening, let's consider a small slice of the fluid, the bit between coordinates x0 and x0 + Δx. This is shown by the dotted lines in the figure.

(b) For this small bit of fluid moving with a velocity v, what is the magnitude and direction of the drag force acting on it?

(c) In order to maintain the fluid moving at a constant speed, the pressure must change along the pipe. Explain why.

(d) Suppose the pressure along the pipe varies as a function of x by some (unknown) function, p(x). Find an expression for the change in pressure

p(x0 + Δx) - p(x0)

in terms of the symbols we have specified.

(e) Show that a linear function satisfies that change equation you obtained in (c). If you can find an appropriate linear function, do so. If you can't, explain why not.

(f) For a pipe of length L, use your results from (d) to show that the flow of matter through the pipe (I) is related to the pressure drop across the pipe [Δp= p(L) - p(0)] by an equation of the form Δp = IR where R is the resistance of the pipe (not the radius). Discuss the dependence of R on the parameters of the problem and whether your result for the various dependences of R is plausible.

(The resulting equation is known as the Hagen-Poieseulle equation in fluid dynamics and it holds even when a more careful model of laminar flow is used.)

This page prepared by

Edward F. Redish
Department of Physics
University of Maryland
College Park, MD 20742
Phone: (301) 405-6120
Email: redish@umd.edu

Last revision 29. December, 2010.